Визуализация примитивов

2.6. Треугольники

Для визуализации наборов треугольников с различной топологией в XNA Framework имеется три типа примитивов: PrimitiveType.TriangleList, PrimitiveType.TriangleFan и PrimitiveType.TriangleStrip.Начнем с самого простого примитива, PrimitiveType.TriangleList.

2.6.1. Несвязанные треугольники (PrimitiveType.TriangleList)

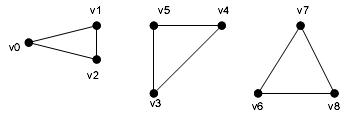
Этот примитив предназначен для визуализации набора несвязанных треугольников: первый треугольник строится с использованием 0-й, 1-й и 2-й вершин, второй треугольник – 3-й, 4-й и 5-й вершин, третий треугольник – 6-й, 7-й и 8-й вершин и т.д. (рисунок 2.21).

Рис. 2.21. Треугольники, нарисованные с использованием примитива PrimitiveType.TriangleList

По умолчанию XNA Framework отображает на экране только те треугольники, вершины которых расположены на экране по часовой стрелке. К примеру, при визуализации треугольников, изображенных на рисунке 2.21 на экране отобразятся только крайние треугольники ( v0, v1, v2 ) и ( v6, v7, v8 ). А вот средний треугольник ( v3, v4, v5 ) будет отброшен, так как его вершины перечисляются против часовой стрелки. Такое на первый взгляд странное поведение XNA Framework обусловлено особенностью отсечения невидимых треугольников в трехмерных сценах. Однако при визуализации двухмерных изображений эта функциональность оказывается не только излишней, но и вредной. Поэтому разработчики XNA Framework заботливо предусмотрели свойство GraphicsDevice.RenderState.CullMode, управляющее режимами отсечения треугольников:

public CullMode CullMode { get; set; }

Это свойство может принимать следующие значения перечислимого типа CullMode:

• CullMode.None - отсечение выключено
• CullMode.Clockwise - отсекаются треугольники, вершины которых расположены на экране по часовой стрелке
• CullMode.CounterClockwise - отсекаются треугольники, у которых вершины расположены на экране против часовой стрелки.

По умолчанию свойству GraphicsDevice.RenderState.CullMode присваивается значение CullMode.CounterClockwise, то есть видеокарта отбрасывает все треугольники, у которых вершины расположены против часовой стрелки. Для отключения этой функциональности достаточно присвоить этому свойству значения CullMode.None.

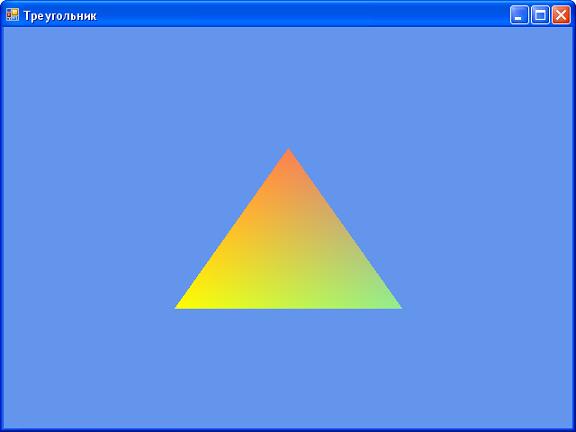
В листинге 2.22 приведен исходный код основных фрагментов программы (Ex12), рисующей в центре экрана треугольник (рисунок 2.22).

Рис. 2.22. Треугольник с разноцветными вершинами

public partial class MainForm : Form 
{
const string effectFileName = "Data
\\ColorFill.fx";
GraphicsDevice device = null; PresentationParameters 
presentParams; Effect effect = null;
VertexDeclaration decl = null; VertexPositionColor[] vertices = null;
FillMode fillMode=FillMode.Solid;
bool closing = false;
…
private void MainFormLoad(object sender, EventArgs e) 
…
{
// Создаем массив для хранения трех вершин треугольника
vertices = new GraphicsBuffer<TransformedColored>(3); 
// Задаем вершины треугольника
vertices[0] = new VertexPositionColor(new Vector3(0.0f, 0.4f, 0.0f),
4> XnaGraphics.Color.Coral);
vertices[1] = new VertexPositionColor(new Vector3(0.4f, -0.4f, 0.0f),
4> XnaGraphics.Color.LightGreen);
vertices[2] = new VertexPositionColor(new Vector3(-0.4f, -0.4f, 0.0f), 
4> XnaGraphics.Color.Yellow); }
private void MainFormPaint(object sender, PaintEventArgs e) 
{
device.Clear(XnaGraphics.Color.CornflowerBlue);
// Выключаем отсечение треугольников
device.RenderState.CullMode = Cull.None;
device.VertexDeclaration = decl;
// Рисуем треугольник
effect.Begin();
foreach (EffectPass pass in effect.CurrentTechnique.Passes)
{
pass.Begin() ;
device.DrawUserPrimitives(PrimitiveType.TriangleList,
 vertices, 0, vertices.Length / 3);
pass.End() ; 
} 
effect.End();
device.Present();
}

Как видно, листинг программы мало чем отличается от предыдущих примеров. Единственное разница заключается в отключении режима отсечения треугольников и использовании примитивов типа PrimitiveType.TriangleList.

Режимы закраски

Как известно, многие приложения 3D моделирования вроде 3ds Max или Maya позволяют отображать сцену в режиме проволочного каркаса ( Wireframe ). Благодаря этому разработчик может ясно видеть топологию сцены, в частности, взаимное расположение всех треугольников на сцене. XNA Framework тоже поддерживает подобную функциональность, позволяя отображать вместо закрашенных треугольников их проволочный каркас. Управление этой функциональностью осуществляется при помощи свойства RenderState.FillMode класса GraphicsDevice:

FillMode FillMode { get; set; }

Свойство может принимать следующие значения перечислимого типа FillMode:

• FillMode.Point - визуализируются только точки, расположенные на вершинах треугольника. Визуализируемые точки являются полноценными точками XNA Framework: к примеру, их размер можно изменять при помощи свойства device.RenderState. PointSize.
• FillMode.WireFrame - визуализирует каркас треугольника, который рисуется с использование oбычных линий вроде TrianglePrimitive.LineList или TrianglePrimitive.LineStrip.
• FillMode.Solid - закрашивает внутреннюю область треугольника.

По умолчанию свойству RenderState.FillMode присвоено значение FillMode.Solid, то есть треугольники рисуются закрашенными.

Для демонстрации практического использования свойства FillMode мы добавим в нашу программу ( Ex12 ) возможность циклической смены режимов отображения треугольников при помощи клавиши пробел (листинг 2.23).

public partial class MainForm : Form
{
// Режим отображения треугольников
FillMode fillMode=FillMode.Solid; 
...
private void MainForm_Paint(object sender, PaintEventArgs e) 
{ 
...
 // Выключаем отсечение треугольников
device.RenderState.CullMode = Cull.None; 
// Задаем режим отображения треугольников
device.RenderState.FillMode = fillMode; 
// Зазаем размер точек
device.RenderState.PointSize = 3.0f;
 ... 
// Рисуем треугольник
effect.Begin();
foreach (EffectPass pass in effect.CurrentTechnique.Passes)
{
pass.Begin();
device.DrawUserPrimitives(PrimitiveType.TriangleList, 
vertices, 0, verteces.Length / 3);
pass.End(); 
}
effect.End();
 ...
}
private void MainForm_KeyDown(object sender, KeyEventArgs e) 
{ 
// Если нажата клавиша пробел
if (e.KeyCode == Keys.Space) 
{ 
// Изменяем режим отображения switch (fillMode) 
{
case FillMode.Point:
fillMode = FillMode.WireFrame; break; case FillMode.WireFrame:
fillMode = FillMode.Solid; break; case FillMode.Solid:
fillMode = FillMode.Point;
break; 
} 
// Перерисовываем экран
Invalidate(); 
} 
 } 
}

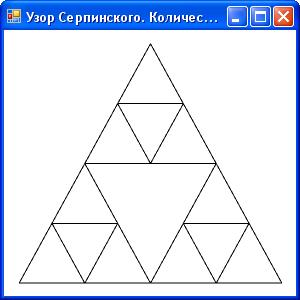
Узор Серпинского

Рис. 2.23. Построение узора Серпинского. Базовый треугольник

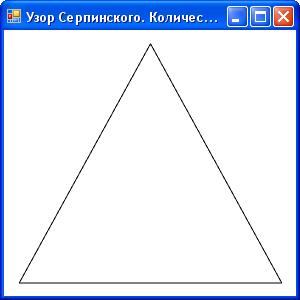
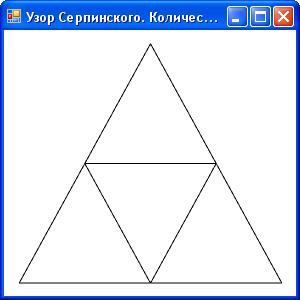
Перейдем к более сложному примеру. Наше следующее приложение будет строить узор Серпинского путем рекурсивного разбиения треугольника, визуализируемого в каркасном режиме. Построение узора начинается с базового треугольника (рисунок 2.23). На первой интеграции в данный большой треугольник вписывается другой треугольник меньшего размера, вершины которого расположены в середине сторон большого треугольника (рисунок 2.24). В результате большой треугольник оказывается как бы разбит на 4 треугольника. На втором этапе данные в три треугольника, примыкающие к вершинам исходного большого треугольника, вписываются по три треугольника (рисунок 2.25). На третьем этапе в образовавшиеся девять треугольников вписываются уже девять треугольников (рисунок 2.26), на четвертом этапе вписывается уже 27 треугольников и так далее. В идеале процесс должен продолжаться до бесконечности, одна ко на практике вполне можно ограничиться десятком итераций (рисунок 2.27), так как размер треугольников, генерируемых в последующих итерациях, будет уже меньше размера пикселей экрана.

Рис. 2.24. Построение узора Серпинского. Первая итерация

Рис. 2.25. Построение узора Серпинского. Вторая итерация

Рис. 2.26. Построение узора Серпинского. Третья итерация

Рис. 2.27. Узор Серпинского, 11 итераций

Так как приложение будет визуализировать десятки или даже сотни тысяч треугольников, очень важно поместить их в единый массив и вывести одним вызовом метода DrawUserPrimitives. Однако для создания такого массива очень полезно заранее знать количество треугольников, которые будут визуализированы за n итераций. Это поможет нам избежать многочисленных изменений размера массива по мере генерации треугольников. Давайте попробуем найти зависимость числа визуализируемых треугольников от количества интеграций. И так, при нулевом количестве итераций мы визуализируем 1 треугольник. При одной итерации число треугольников становится 1 + 1 = 2. При двух итерациях количество треугольников будет равно 1 + 1 + 3 = 5, при трех 1 + 1 + 3 + 9 = 14. Таким образом, мы можем вывести некоторую общую закономерность для n итераций:

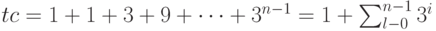( 2.4)

где

• tc - количество треугольников, визуализируемых при n итераций.

В принципе, это выражение вполне приемлемо, однако знак суммы смотрится не особо красиво. Однако открыв учебник высшей математики вроде можно найти весьма интересное соотношение:

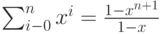( 2.5)

Соответственно, выражение 2.4 можно переписать без использования n элементов:

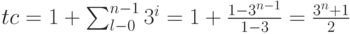( 2.6)

Гораздо более наглядное выражение, не так ли? Однако так как разные видеокарты могут визуализировать разное число треугольников, не исключено, что приложению придется решать и образную задачу. Допустим, мы определим в приложении число итераций ( n ) равным 11, то есть узор Серпинского будет содержать 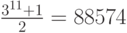треугольников с общим количеством вершин 88574 ? 3 = 265722. Но ведь некоторые видеокарты могут оказаться не способными визуализировать такое количество треугольников за один присест. Как приложение должно повести себя в подобном случае? Наиболее простое решение – сократить количество интеграций до максимально приемлемого. А для этого нам придется определять максимальное количество итераций ( n ), при котором количество треугольников не превышает заданное значение tc. Для этого выражение (2.6) достаточно переписать как

( 2.7)

после чего взять от обоих частей выражения логарифм по основанию 3:

( 2.8)

где

• - функция, возвращающая целое число, не превышающее x (то аналог метода Math.Floor из C#).

К слову

Согласно выражению 2.8 на компьютере с Intel GMA 900 приложение может выполнить до 9-ти итераций, на NVIDIA NV 2x-3x до 12-ти итераций, а на ATI R2xx-R5xx до 13-ти итераций.

После такого небольшого математического экскурса можно приступать реализации нашего приложения. Визуализация треугольников будет осуществляться в два этапа:

1. Заполнение графического буфера информацией о треугольниках.
2. Визуализация треугольников одним вызовом метода DrawUserPrimitives.

Вычисление координат треугольников мы организуем с использованием рекурсивной функции DrawTriangle принимающей в качестве параметров координаты треугольника и количество оставшихся итераций. Эта функция будет помещать в массив вершин координаты текущего треугольника, после чего выполнять деление этого треугольника на три части и вызывать саму себя для этих частей, но уже с уменьшенным количеством оставшихся итераций на 1. Процесс повторяется до тех пор, пока количество оставшихся итераций не достигнет 0.

Исходный код основных фрагментов программы с подробными комментариями приведен в листинге 2.24.

// Примем Examples\Ch02\Ex13
public partial class MainForm : Form
{
// Число итераций для визуализации треугольника Серпинского. 
Если видеокарта не способна
// визуализировать такое количество треугольников, 
число итераций автоматически уменьшается
// до приемлемого значения
const int n = 15;
const string effectFileName = "Data
\\ColorFill.fx";
GraphicsDevice device = null; PresentParameters presentParams; 
Effect effect = null; VertexDeclaration decl = null;
// Массив вершин узора Серпинского
VertexPositionColor[] vertices = null; 
// Индекс текущей вершины (глобальная переменная, 
используемая при рекурсивном формировании 
// узора Серпинского)
int currentVertex;
// Рекурсивная функция, заносящая в массив
 vertices информацию о вершинах узора. 
// a, b, c - координаты текущего треугольника 
// pass - число оставшихся итераций
void DrawTriangle(Vector2 a, Vector2 b, Vector2 c, int pass) 
{ 
// Если это последняя итерация, выходим из функции 
if (pass <= 0) 
return;
// Уменьшаем количество оставшихся итераций pass -= 1;
// Помещаем в массив вершины треугольника
 вписанного в текущий "большой" треугольник
vertices[currentVertex] = new VertexPositionColor
(new Vector3(ab.X, ab.Y, 0.0f),
 XnaGraphics.Color.Black);
vertices[currentVertex + 1] = new VertexPositionColor
(new Vector3(ac.X, ac.Y, 0.0f),
 XnaGraphics.Color.Black);
vertices[currentVertex + 2] = new VertexPositionColor
(new Vector3(bc.X, bc.Y, 0.0f),
XnaGraphics.Color.Black);
// Увеличиваем индекс текущей вершины currentVertex += 3;
// Вычисляем координаты середины сторон	треугольника
Vector2 ab = new Vector2((a.X +	b.X) / 2.0f,(a.Y+b.Y)/2.0f);
Vector2 ac = new Vector2((a.X +	c.X) / 2.0f,(a.Y+c.Y)/2.0f);
Vector2 bc = new Vector2((b.X +	c.X) / 2.0f,(b.Y+c.Y)/2.0f);
// Вызываем этот рекурсивный метод для 
образовавшихся трех крайних треугольников, примыкающих 
// к углам текущего треугольника
DrawTriangle(a, ab, ac, pass);
DrawTriangle(b, ab, bc, pass);
DrawTriangle(c, ac, bc, pass); 
}
private void MainForm_Load(object sender, EventArgs e) 
{ 
...
// Определяем максимальное количество треугольников,
 которое текущая видеокарта может 
// визуализировать за один присест
int maxTriangleCount = Math.Min(device.GraphicsDevice
Capabilities.MaxPrimitiveCount,
device.GraphicsDeviceCapabilities.MaxVertexIndex / 3);
// Вычисляем по формуле 2.8 максимальное количество
 итераций визуализации узора, которые 
// можно выполнить на текущей видеокарте
int maxPass = (int) Math.Floor(Math.Log(2 * maxTriangleCount - 1, 3)); 
// При необходимости уменьшаем количество интеграций,
 которое задаются константой n
int passes = Math.Min(n, maxPass); 
// Вычисляем по формуле 2.6 количество треугольников, 
формирующих данный узор Серпинского.
int triangleCount = ((int)Math.Pow(3, passes) + 1) / 2;
// Выделяем память для хранения информации о вершинах 
треугольниках vertices = new VertexPositionColor[3 * triangleCount];
Text += " Количество итераций: " + passes.ToString();
// Вершины начального треугольника
Vector2 a = new Vector2(0.0f, 0.9f); Vector2 b = new
 Vector2(-0.9f, -0.9f); Vector2 c = new Vector2(0.9f, -0.9f);
// Обнуляем индекс текущей вершины
currentVertex = 0; 
// Заносим в массив вершины самого большого треугольника
vertices[currentVertex] = new
 VertexPositionColor(new Vector3(a.X, a.Y, 0.0f),
XnaGraphics.Color.Black); vertices[currentVertex + 1] = new
VertexPositionColor(new Vector3(b.X, b.Y, 0.0f),
XnaGraphics.Color.Black); vertices[currentVertex + 2] = new
VertexPositionColor(new Vector3(c.X, c.Y, 0.0f),
XnaGraphics.Color.Black); currentVertex += 3;
// Выполняет рекурсивное деление треугольника в течении
 pass итераций CreateTriangle(a, b, c, passes); 
}
private void MainForm_Paint(object sender, PaintEventArgs e) 
{ 
...
// Очищаем экран
device.Clear(ClearFlags.Target, Color.White, 0.0f, 0);
device.BeginScene();
// Отключаем отсечение треугольников
device.RenderState.CullMode = Cull.None; 
// Используем каркасную визуализацию треугольников
device.RenderState.FillMode = FillMode.WireFrame;
device.VertexFormat = TransformedColored.Format;
// Рисуем треугольники
device.DrawUserPrimitives(PrimitiveType.TriangleList, 
verteces.NumberElements/3, verteces);
device.EndScene();
device.Present();
		}

	}
}