НОУ ИНТУИТ | Теория экономических механизмов. Лекция 11: Принцип взаимосвязи

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 05.08.2011 | Доступ: свободный | Студентов: 1543 / 82 | Оценка: 4.50 / 3.50 | Длительность: 18:52:00

ISBN: 978-5-9963-0014-3

Темы: Математика, Экономика

Специальности: Математик, Экономист

|

Вам нравится? Нравится 44 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Обобщение принципа взаимосвязи

Итак, мы хотели бы обобщить принцип взаимосвязи на ситуации, когда некие ненулевые суммы платит не только победитель, но и все остальные участники. Результат получится на удивление просто и будет сильно напоминать теорему 11.1.

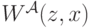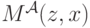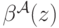Давайте просто вместо функции $W^{\mathcal A}(z,x)$ рассмотрим другую функцию, $M^{\mathcal A}(z,x)$ , которая показывает, какова в аукционе ожидаемая выплата агента, получившего сигнал и делающего ставку $\beta^{\mathcal A}(z)$ , где $\beta^{\mathcal A}$ — симметричная равновесная стратегия аукциона . То есть фактически все то же самое, но теперь мы не предполагаем, что платит только победитель, и вероятность победы этого агента в рассуждениях участвовать не будет. Соответственно, в аукционе, где платит только победитель, ожидаемая выплата будет равна

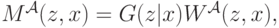
$M^{\mathcal A}(z,x) = G(z|x)W^{\mathcal A}(z,x),$

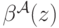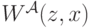потому что G(z|x) — это вероятность выиграть с сигналом и ставкой $\beta^{\mathcal A}(z)$ , а $W^{\mathcal A}(z,x)$ — сумма, которую придется заплатить в случае выигрыша.

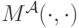Обозначим, как раньше мы делали для $W^{\mathcal A}$ , через $M^{\mathcal A}_2(x,y)$ частную производную функции $M^{\mathcal A}(\cdot,\cdot)$ по второму аргументу, вычисленную в точке (z,x) :

$M^{\mathcal A}_2(z,x) = \left.\frac{\partial M^{\mathcal A}(t,u)}{\partial u}\right|_{(z,x)}.$

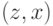Теорема 11.4. (обобщенный принцип взаимосвязи) Пусть и — два аукциона, в которых побеждает наивысшая ставка, причем платить в результате может не только победитель. Пусть в каждом из них есть свое симметричное и возрастающее равновесие, причем:

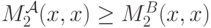для всех $M^{\mathcal A}_2(x,x) \ge M^B_2(x,x)$ ;
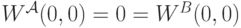выполняется начальное условие $W^{\mathcal A}(0,0) = 0 = W^B(0,0)$ .

Тогда ожидаемый доход аукциона не меньше ожидаемого дохода аукциона .

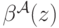Доказательство. В аукционе ожидаемый доход агента с сигналом , который ставит $\beta^{\mathcal A}(z)$ , составит

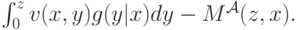
$\int_0^zv(x,y)g(y|x)dy - M^{\mathcal A}(z,x).$

Именно эту величину максимизирует каждый агент. В равновесии оптимально брать 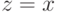z=x , и поэтому

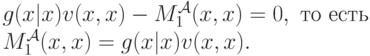
$g(x|x)v(x,x) - M^{\mathcal A}_1(x,x) = 0,\text{ то есть} \\ M^{\mathcal A}_1(x,x) = g(x|x)v(x,x).$

Теперь, определяя, как и в доказательстве теоремы 11.1,

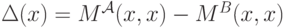
$\Delta(x) = M^{\mathcal A}(x,x)-M^B(x,x)$

получаем, что

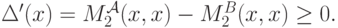
$\Delta^\prime(x) = M^{\mathcal A}_2(x,x) - M^B_2(x,x) \ge 0.$

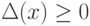Таким образом, $\Delta(x)$ — неубывающая функция, и $\Delta(0)=0$ ; следовательно, $\Delta(x)\ge 0$ на $[0,\omega]$ .

Оставляем читателю в качестве упражнения сравнить при помощи теоремы 11.4 обычный аукцион первой цены и аукцион первой цены, в котором платят все (all-pay auction, который мы описывали в разделе "Теорема об эквивалентности доходности" . В результате должно получиться, что аукцион, в котором платят все, для аукционера выгоднее (его ожидаемый доход больше).

Публичная информация

Напоследок, когда принцип взаимосвязи разобран нами полностью, давайте продвинемся чуть дальше и рассмотрим еще одно небольшое обобщение ситуации аукциона. Предположим, что продавец кое-что знает. Какой-то сигнал , которого не знают агенты-покупатели. То есть теперь

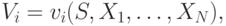
$V_i = v_i(S, X_1,\ldots, X_N),$

что в симметричном случае превращается в

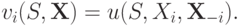
$v_i(S,\mathbf X) = u(S,X_i,\mathbf X_{-i}).$

Предположим, что 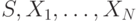$S,X_1,\ldots,X_N$ аффилированы и распределены с совместной плотностью , которая симметрична по последним аргументам (то есть симметрична по X_i , но может оказаться несимметричной для ).

Вопрос перед нами стоит весьма практический: стоит ли продавцу сообщать агентам имеющуюся у него информацию? Если продавец свой сигнал не сообщает, то этот сигнал просто можно получить интегрированием (маргинализовать) из всех выражений. Грубо говоря (проверьте это формально!), все формулы, которые мы писали выше, получат дополнительный интеграл по сверху, но не будет вообще участвовать в подынтегральном выражении. И просто все получится как раньше:

$v(x,y) = \mathbf E\left[\vphantom{1^2}V_1|X_1 = x, Y_1 = y\right].$

А вот если продавец информацию сообщит, то все получится уже совсем по-другому. Давайте предположим, что продавец просто всегда сообщает свой сигнал всем агентам. Обозначим тогда через

$\hat v(s,x,y) = \mathbf E\left[\vphantom{1^2}V_1|S = s, X_1 = x, Y_1 = y\right]$

ожидание ценности агента 1 для публичного сигнала , приватного сигнала и наибольшего из остальных .

По симметрии, эти функции одинаковы для всех агентов; по аффилированности, 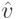$\hat v$ возрастает; кроме того, 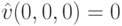$\hat v(0,0,0)=0$ . Соответственно,

$v(x,y) = \mathbf E\left[\vphantom{1^2}\hat v(s,x,y)|X_1 = x, Y_1 = y\right].$

Для начала возьмем аукцион первой цены. Мы будем рассматривать два разных аукциона: в первом из них агентам говорят , а во втором — не говорят. Оба — первой цены. Давайте сравним их доходность.

Когда не сообщают, все как раньше:

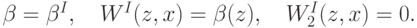
$\beta=\beta^I,\quad W^I(z,x) = \beta(z),\quad W^I_2(z,x) = 0.$

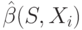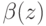А когда сообщают, получается равновесная стратегия $\hat\beta(S,X_i)$ , возрастающая от обеих переменных. И тогда ожидаемый доход победителя с сигналом и ставкой $\beta(z)$ будет составлять

$\hat W^1(z,x) = \mathbf E\left[\vphantom{1^2}\hat\beta(S,z) | X_1 = x\right].$

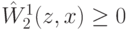А поскольку и X_1 аффилированы, $\hat W^1_2(z,x) \ge 0$ .

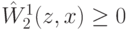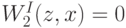Получается, что $\hat W^1_2(z,x) \ge 0$ , а W^I_2(z,x) = 0 . То есть продавцу всегда выгодно сообщать имеющуюся у него информацию.

То же самое верно для аукциона второй цены и для английского аукциона, в рассуждениях практически ничего не меняется.

Замечание. Мы здесь провели только "эвристическую" часть поиска равновесной стратегии. Чтобы доказать, что 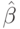$\hat\beta$ — равновесная стратегия, надо еще проверить, что 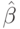$\hat\beta$ действительно существует. Именно это мы всегда делали после того, как получали общий вид равновесной стратегии; здесь это делается совершенно обычным образом, и мы не будем приводить строгое доказательство — рекомендуем читателю поупражняться.

Дальше >>

Авторизоваться

Теория экономических механизмов

Принцип взаимосвязи

Обобщение принципа взаимосвязи

Публичная информация

Вопросы и ответы