Аукционы с зависимыми ценностями
Аффилированные сигналы
Итак, отныне мы отказываемся от предположения, что распределения  независимы, и будем считать, что они могут быть коррелированными. В таком случае появляется единая совместная плотность
независимы, и будем считать, что они могут быть коррелированными. В таком случае появляется единая совместная плотность  , неравная
, неравная  . Конечно, работать с совсем уж произвольным распределением вероятностей нелегко, и многого о нем доказать не получится. Да и на практике предположение, которое мы сейчас сделаем, представляется в высшей степени разумным. Мы будем предполагать, что сигналы
. Конечно, работать с совсем уж произвольным распределением вероятностей нелегко, и многого о нем доказать не получится. Да и на практике предположение, которое мы сейчас сделаем, представляется в высшей степени разумным. Мы будем предполагать, что сигналы  аффилированы.
аффилированы.
Определение 9.1. Случайные величины  называются аффилированными, если
называются аффилированными, если  :
:

где
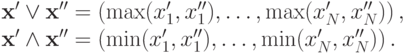
Аффилированность — это усиленная форма положительной корреляции. По сути она означает, что если некоторая часть значений  велика, то остальные значения тоже, скорее всего, будут велики. Согласитесь, что для аукционов с месторождениями, да и вообще для типичной ситуации аукциона с зависимыми ценностями, это предположение выглядит разумным.
велика, то остальные значения тоже, скорее всего, будут велики. Согласитесь, что для аукционов с месторождениями, да и вообще для типичной ситуации аукциона с зависимыми ценностями, это предположение выглядит разумным.
Рассмотрим еще одно сугубо математическое определение.
Определение 9.2. Функция  называется супермодулярной, если
называется супермодулярной, если  :
:

Из определений 9.1 и 9.2 мгновенно следует, что компоненты вектора случайных величин  аффилированы тогда и только тогда, когда
аффилированы тогда и только тогда, когда  супермодулярна. Чтобы убедиться в этом, достаточно прологарифмировать равенство из определения аффилированной функции. Следующее предложение мы также оставим без доказательства — доказать его будет хорошим упражнением.
супермодулярна. Чтобы убедиться в этом, достаточно прологарифмировать равенство из определения аффилированной функции. Следующее предложение мы также оставим без доказательства — доказать его будет хорошим упражнением.
Предложение 9.1. Если  — гладкая функция, то
— гладкая функция, то  супермодулярна тогда и только тогда, когда
супермодулярна тогда и только тогда, когда

Сейчас мы будем понемножку устанавливать математические факты о супермодулярных функциях и аффилированных случайных переменных, которые нам потребуются в дальнейшем. Поэтому нетерпеливый читатель может сейчас пропустить остаток этого раздела и возвращаться к нему по мере надобности, когда мы в последующем тексте будем на него ссылаться. Но для полноты картины все же рекомендуем читать по порядку.
Рассмотрим переменные  , которые мы уже использовали в предыдущих лекциях. Напомним, что они представляют собой сигналы
, которые мы уже использовали в предыдущих лекциях. Напомним, что они представляют собой сигналы  , упорядоченные в порядке убывания значений.
, упорядоченные в порядке убывания значений.
Совместная плотность  случайных величин
случайных величин  легко выражается через совместную плотность вектора сигналов
легко выражается через совместную плотность вектора сигналов  . Для этого достаточно заметить, что каждый вектор
. Для этого достаточно заметить, что каждый вектор  соответствует
соответствует  ! различных векторов
! различных векторов  : можно перемешать компоненты
: можно перемешать компоненты  как угодно, а получаться все равно будет один и тот же упорядоченный вектор. Поэтому
как угодно, а получаться все равно будет один и тот же упорядоченный вектор. Поэтому

Значит, если переменные 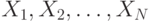 аффилированы, то аффилированными также будут и
аффилированы, то аффилированными также будут и  .
.
Введем теперь новое определение.
Определение 9.3. Рассмотрим две случайные переменные —  и
и  — с функциями распределения
— с функциями распределения  и
и  и плотностями распределения
и плотностями распределения  и
и  соответственно. Говорят, что:
соответственно. Говорят, что:
-
 доминирует над
доминирует над  в терминах отношения правдоподобия (like-li-hood ratio), если функция отношения правдоподобия
в терминах отношения правдоподобия (like-li-hood ratio), если функция отношения правдоподобия  возрастает, то есть
возрастает, то есть
-
 доминирует над
доминирует над  в терминах доли риска (hazard rate), если доля риска у
в терминах доли риска (hazard rate), если доля риска у  всегда выше, чем у
всегда выше, чем у  :
:
-
 доминирует над
доминирует над  в терминах обратной доли риска (reverse hazard rate), если обратная доля риска у
в терминах обратной доли риска (reverse hazard rate), если обратная доля риска у  всегда выше, чем у
всегда выше, чем у  :
:
-
 стохастически доминирует над
стохастически доминирует над  , если
, если .
.
Предложение 9.2.
- Если
 доминирует над
доминирует над  в терминах отношения правдоподобия, то
в терминах отношения правдоподобия, то  доминирует над
доминирует над  в терминах доли риска.
в терминах доли риска. - Если
 доминирует над
доминирует над  в терминах отношения правдоподобия, то
в терминах отношения правдоподобия, то  доминирует над
доминирует над  в терминах обратной доли риска.
в терминах обратной доли риска. - Если
 доминирует над
доминирует над  в терминах доли риска, то
в терминах доли риска, то  стохастически доминирует над
стохастически доминирует над  .
.
Доказательство.
- Доминирование в терминах отношения правдоподобия означает, что
 .
.Это эквивалентно тому, что
 .
.Проинтегрируем последнее выражение по
 :
: ,
,или, что то же самое,
 .
. - Как и в первом пункте,
 .
.Но теперь мы это перепишем слегка по-другому:
 .
.Снова взяв интеграл, но на этот раз по
 , получаем:
, получаем: ,
,или, что то же самое,
 .
. - Как известно, функцию распределения
 можно переписать в терминах доли риска
можно переписать в терминах доли риска 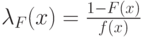 :
: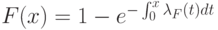
(если вам это неизвестно, проверьте сами!). Из этого равенства очевидно, что если для всех

 , то и для самих функций распределения
, то и для самих функций распределения  для всех значений
для всех значений  .
.
Рассмотрим теперь две переменные —  и
и  — с совместной плотностью
— с совместной плотностью
![f:[0,\omega]\times[0,\omega]\to\mathbb R](/sites/default/files/tex_cache/41b7b87f9966f8ef6a18227465b15d44.png)
и, соответственно, функцией совместного распределения
![F:[0,\omega]\times[0,\omega]\to\mathbb R](/sites/default/files/tex_cache/db6b95ac190160c2441923a0d39e08e5.png) .
.
Если  и
и  аффилированы, то
аффилированы, то
 .
.
Преобразуем это соотношение:

Последнее равенство означает, что функция отношения правдоподобия

возрастает для всех  , то есть
, то есть  доминирует над
доминирует над 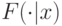 в терминах отношения правдоподобия для всех
в терминах отношения правдоподобия для всех  . А значит, по предложению 9.2,
. А значит, по предложению 9.2,  в таких случаях доминирует над
в таких случаях доминирует над 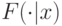 и в терминах доли риска, и в терминах обратной доли риска, и стохастически.
и в терминах доли риска, и в терминах обратной доли риска, и стохастически.
Из стохастического доминирования следует, что для всех  функция
функция  является неубывающей (поскольку стохастическое доминирование означает, что
является неубывающей (поскольку стохастическое доминирование означает, что  для любых
для любых  ). А это, в свою очередь, означает, что условное математическое ожидание
). А это, в свою очередь, означает, что условное математическое ожидание ![\mathbf E[Y | X = x^\prime]](/sites/default/files/tex_cache/ed28feb3cd8bef65f7b24f2d6cc6c757.png) тоже является неубывающим как функция от
тоже является неубывающим как функция от  . Отсюда, в частности, следует, что в таком случае величины
. Отсюда, в частности, следует, что в таком случае величины  и
и  положительно коррелируют (так мы доказали, что аффилированность — более сильное понятие, чем положительная корреляция). На самом же деле верно и более сильное утверждение: для всякой неубывающей функции
положительно коррелируют (так мы доказали, что аффилированность — более сильное понятие, чем положительная корреляция). На самом же деле верно и более сильное утверждение: для всякой неубывающей функции  условное ожидание
условное ожидание
![\mathbf E[\gamma(Y) | X = x ]](/sites/default/files/tex_cache/76201692af2fd099c7392e2bd8b74e22.png)
не убывает как функция от  (оставляем доказательство читателю в качестве упражнения).
(оставляем доказательство читателю в качестве упражнения).
Итак, вернемся теперь к нашим аукционам. Если сигналы агентов  аффилированы, то, следовательно,
аффилированы, то, следовательно,  также будут аффилированы.
также будут аффилированы.
Пусть  и
и 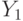 аффилированы. Если
аффилированы. Если  — это распределение
— это распределение 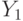 , то при условии, что
, то при условии, что 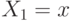 и
и  ,
, 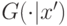 доминирует над
доминирует над  в терминах обратной доли риска:
в терминах обратной доли риска:
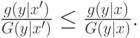
Более того, для всякой возрастающей функции  , если
, если  , то
, то
![\mathbf E\left[\vphantom{1^2}\gamma(Y_1) | X_1 = x^\prime \right] \ge \mathbf E\left[\vphantom{1^2}\gamma(Y_1) | X_1 = x\right].](/sites/default/files/tex_cache/60dce0790e9142684b8c31ec56d21ed2.png)
Вот такие следствия нам удалось извлечь из свойства аффилированности неточных сигналов агентов. В скором времени мы их применим.
