Теоремы Эрроу и Гиббарда-Саттертуэйта
Другие доказательства теоремы Эрроу
Доказательство теоремы 6.1 получилось довольно громоздким и техническим. Конечно, на самом деле это идейное доказательство: мы постепенно получали все более и более сильные свойства определяющих наборов, пока не выяснили, что на самом деле среди них есть одноэлементные множества.
Но можно предложить и другие идейные доказательства, например [7]. В этом параграфе, основанном на работе [21], мы рассмотрим три альтернативных (и достаточно коротких) доказательства теоремы Эрроу. Надеемся, их идеи окажутся достаточно различными, чтобы оправдать такой подход. %Рекомендуем читателю по мере разбора этих доказательств по крайней мере отмечать, %где в каждом из них используется, что альтернатив по меньшей мере три.
Первое доказательство теоремы 6.1. Это доказательство тоже будет проведено в несколько шагов, но на этот раз шаги куда быстрее приведут к цели. Правда, по сравнению с исходным доказательством они могут показаться менее очевидными. Основным для доказательства здесь станет доказательство существования ключевого агента (pivotal agent): агента, который может изменением своего решения изменить результат функции социального выбора.
- Если в некотором профиле
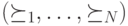 некий исход
некий исход 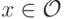 для каждого агента
для каждого агента  находится на самом верху или в самом низу (то есть
находится на самом верху или в самом низу (то есть 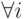
 или
или 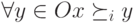 ), то в результате ранжирования функция социального выбора также должна поместить
), то в результате ранжирования функция социального выбора также должна поместить  на одну крайних позиций.
на одну крайних позиций.Доказательство очень простое. Предположим, что это не так, то есть
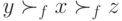 для некоторых
для некоторых 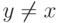 ,
,  . Поскольку
. Поскольку  у каждого находится в одной из крайних позиций, мы можем, не нарушая никаких индивидуальных предпочтений, переместить в предпочтениях каждого агента
у каждого находится в одной из крайних позиций, мы можем, не нарушая никаких индивидуальных предпочтений, переместить в предпочтениях каждого агента  над
над  (проверьте, что это возможно!). Тогда по транзитивности
(проверьте, что это возможно!). Тогда по транзитивности  , но единогласное решение агентов гласит, что
, но единогласное решение агентов гласит, что  . Противоречие.
. Противоречие. - Для каждого из исходов
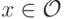 существует такой ключевой агент
существует такой ключевой агент  , что для некоторого профиля предпочтений, в котором
, что для некоторого профиля предпочтений, в котором  обладает вышеописанным свойством, он может переместить
обладает вышеописанным свойством, он может переместить  снизу вверх в результате функции социального выбора, изменив только свой профиль.
снизу вверх в результате функции социального выбора, изменив только свой профиль.Пусть каждый агент поставит
 в самый низ. По анонимности,
в самый низ. По анонимности,  должен занимать последнюю позицию. Теперь пусть агенты по одному перемещают
должен занимать последнюю позицию. Теперь пусть агенты по одному перемещают  с самого низа на самый верх. Рано или поздно
с самого низа на самый верх. Рано или поздно  переместится и, по пункту
переместится и, по пункту  ,
,  переместится сразу на самую верхнюю позицию. Вот последний перед этим профиль предпочтений и соответствующего агента мы и выберем.
переместится сразу на самую верхнюю позицию. Вот последний перед этим профиль предпочтений и соответствующего агента мы и выберем. - Агент
 является диктатором для каждой пары исходов
является диктатором для каждой пары исходов 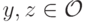 , не включающей в себя
, не включающей в себя 
Выберем элемент
 — один из этой пары — и рассмотрим профиль из пункта
— один из этой пары — и рассмотрим профиль из пункта  , для которого агент
, для которого агент  может переместить
может переместить  снизу вверх. Пусть теперь
снизу вверх. Пусть теперь  изменит свой профиль, переместив
изменит свой профиль, переместив  на самый верх:
на самый верх: 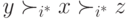 . Рассмотрим всевозможные профили других агентов, в которых
. Рассмотрим всевозможные профили других агентов, в которых  и
и  меняются местами произвольно, но
меняются местами произвольно, но  остается на своих крайних позициях. По свойству попарной независимости, результат на этих профилях должен быть
остается на своих крайних позициях. По свойству попарной независимости, результат на этих профилях должен быть  , потому что относительные позиции
, потому что относительные позиции  и
и  такие же, как в том профиле, когда
такие же, как в том профиле, когда  у
у  был в самом низу, и в результате
был в самом низу, и в результате  тоже был в самом низу. Аналогично, в результате должно быть
тоже был в самом низу. Аналогично, в результате должно быть  . Соответственно, по транзитивности должно быть
. Соответственно, по транзитивности должно быть  . Но эта конструкция не зависела от относительного расположения
. Но эта конструкция не зависела от относительного расположения  и
и  у других агентов! Иными словами,
у других агентов! Иными словами,  тогда и только тогда, когда
тогда и только тогда, когда 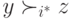 .
. - Агент
 является диктатором для любой пары исходов
является диктатором для любой пары исходов 
Рассмотрим третью возможность
 , не входящую в эту пару. Для нее должен быть какой-нибудь диктатор
, не входящую в эту пару. Для нее должен быть какой-нибудь диктатор 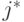 . Он должен быть диктатором для каждой пары, не содержащей
. Он должен быть диктатором для каждой пары, не содержащей  , например для
, например для 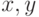 . Но
. Но  может изменить судьбу пары
может изменить судьбу пары 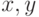 , потому что он может при определенных обстоятельствах переместить
, потому что он может при определенных обстоятельствах переместить  с самого низа на самый верх. Значит,
с самого низа на самый верх. Значит, 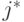 и
и  — одно лицо.
— одно лицо.
Второе доказательство теоремы 6.1. Второе доказательство (как, собственно, и третье) тоже будет строить агента-диктатора. Но делать это мы будем уже другим способом. Давайте рассмотрим парадокс Кондорсе и впишем его в профили агентов. Обозначим возможные исходы в алфавитном порядке через  . Все агенты в так называемых профилях Кондорсе будут иметь профили одного из
. Все агенты в так называемых профилях Кондорсе будут иметь профили одного из  типов:
типов: 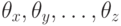 . Предпочтения этих типов будут выглядеть так:
. Предпочтения этих типов будут выглядеть так:

То есть это просто упорядоченная в алфавитном порядке последовательность исходов, сдвинутая циклически так, чтобы в профиле типа 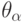 исход
исход  оказался бы на первом месте.
оказался бы на первом месте.
Если все агенты имеют тип 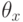 , то, по принципу единогласия,
, то, по принципу единогласия, 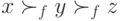 . Рассмотрим все возможные векторы профилей агентов и выберем из них тот, где число агентов типа
. Рассмотрим все возможные векторы профилей агентов и выберем из них тот, где число агентов типа 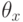 минимально, но результат все равно имеет тип
минимально, но результат все равно имеет тип 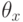 . Обозначим этот профиль через
. Обозначим этот профиль через 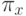 . Хотя бы один агент
. Хотя бы один агент  , имеющий тип
, имеющий тип 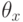 , должен существовать в
, должен существовать в 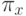 , т. к. если никто из агентов не этого типа, то по принципу единогласия
, т. к. если никто из агентов не этого типа, то по принципу единогласия 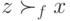 .
.
Теперь докажем, что  может в профиле
может в профиле 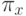 творить вообще все что хочет. Предположим, что исход
творить вообще все что хочет. Предположим, что исход  следует по алфавиту сразу за исходом
следует по алфавиту сразу за исходом  , и в профиле
, и в профиле 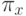 агент
агент  меняет свой тип на
меняет свой тип на  , и в результате получается профиль Кондорсе
, и в результате получается профиль Кондорсе 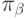 . По свойству попарной независимости, все равно в новом профиле
. По свойству попарной независимости, все равно в новом профиле 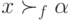 и
и  . Значит, чтобы порядок изменился (а он должен измениться, ведь мы взяли минимальное возможное число агентов типа
. Значит, чтобы порядок изменился (а он должен измениться, ведь мы взяли минимальное возможное число агентов типа 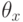 ), нужно, чтобы в результате было верно
), нужно, чтобы в результате было верно 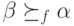 (а если
(а если 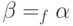 , то по транзитивности должно быть
, то по транзитивности должно быть  ).
).
Пусть  изменит свой профиль на
изменит свой профиль на 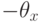 , то есть на профиль вида
, то есть на профиль вида
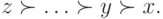
Получится уже не профиль Кондорсе  . Рассмотрим любые два исхода
. Рассмотрим любые два исхода 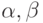 , идущие друг за другом по алфавиту. Тогда
, идущие друг за другом по алфавиту. Тогда  и
и 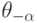 совпадают на паре
совпадают на паре 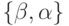 (в обоих
(в обоих  ) и на паре
) и на паре 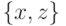 (в обоих
(в обоих  ). Значит, по независимости, на профиле
). Значит, по независимости, на профиле 
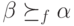 , потому что так было в профиле
, потому что так было в профиле 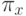 . Но поскольку
. Но поскольку  и
и  произвольные, то, значит, в профиле
произвольные, то, значит, в профиле 
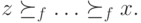
Более того, если бы было верно, что  в профиле
в профиле  , то они были бы равны и в профиле
, то они были бы равны и в профиле 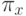 , и, значит, было бы верно, что
, и, значит, было бы верно, что  в профиле
в профиле 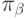 , а значит, и в профиле
, а значит, и в профиле  , что приводит к противоречию. Значит, все неравенства строгие:
, что приводит к противоречию. Значит, все неравенства строгие:
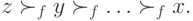
Теперь покажем, что  — диктатор в каждом профиле, не только в
— диктатор в каждом профиле, не только в 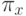 . Предположим, что в некотором профиле
. Предположим, что в некотором профиле  агент
агент  является диктатором, то есть при условии, что предпочтения остальных соответствуют профилю
является диктатором, то есть при условии, что предпочтения остальных соответствуют профилю  , агент
, агент  может добиться любого желаемого решения. Мы это про агента
может добиться любого желаемого решения. Мы это про агента  уже доказали для профиля
уже доказали для профиля 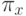 . Изменим тогда
. Изменим тогда  на
на 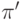 , позволив ровно одному агенту
, позволив ровно одному агенту 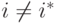 поднять ровно одну альтернативу на полшага выше: либо разрешить ничью между
поднять ровно одну альтернативу на полшага выше: либо разрешить ничью между  и
и  , либо ее создать, но не то и другое вместе, и других альтернатив менять тоже не позволим. Предположим, что для
, либо ее создать, но не то и другое вместе, и других альтернатив менять тоже не позволим. Предположим, что для 
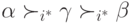 в профиле
в профиле  . Тогда, значит, и в результате профиля
. Тогда, значит, и в результате профиля 
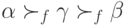 (ведь
(ведь  там диктатор). Следовательно, и в
там диктатор). Следовательно, и в 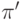
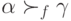 и
и 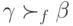 , а это значит, что по транзитивности
, а это значит, что по транзитивности  .
.
А по принципу единогласия это значит, что те полшага, которые сделал агент  в профиле
в профиле 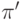 , ничего для
, ничего для  изменить не смогли: в
изменить не смогли: в 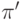 агент
агент  является таким же диктатором, каким был и в профиле
является таким же диктатором, каким был и в профиле  . Но это значит, что
. Но это значит, что  — диктатор везде, ведь из любого профиля в любой другой можно придти последовательностью таких шажков (проверьте!).
— диктатор везде, ведь из любого профиля в любой другой можно придти последовательностью таких шажков (проверьте!).
Итак, второе доказательство использовало специальный вид профилей предпочтений агентов — обобщение парадокса Кондорсе. Третье, самое короткое, будет весьма интересным — мы докажем лемму о том, как должны соотноситься между собой разные предпочтения.
Лемма 6.1. (о строгой нейтральности) Рассмотрим две пары альтернатив  и
и 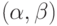 . Предположим, что предпочтения каждого агента на этих парах совпадают, и все такие предпочтения являются строгими. Тогда предпочтения на выходе функции социального выбора на этих парах тоже будут совпадать и тоже будут строгими. Это выполняется для каждой функции социального выбора.
. Предположим, что предпочтения каждого агента на этих парах совпадают, и все такие предпочтения являются строгими. Тогда предпочтения на выходе функции социального выбора на этих парах тоже будут совпадать и тоже будут строгими. Это выполняется для каждой функции социального выбора.
Доказательство. Если пары  и
и 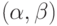 идентичны, то утверждение очевидно. Рассмотрим случай, когда они не совпадают. Предположим без потери общности, что
идентичны, то утверждение очевидно. Рассмотрим случай, когда они не совпадают. Предположим без потери общности, что  . Переместим
. Переместим  (если оно не равно
(если оно не равно  ) в позицию непосредственно сверху
) в позицию непосредственно сверху  для каждого агента, а
для каждого агента, а  — в позицию непосредственно снизу
— в позицию непосредственно снизу  для каждого агента (если, конечно,
для каждого агента (если, конечно, 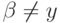 ). Поскольку все предпочтения строгие, это можно сделать, не нарушив относительного расположения пар
). Поскольку все предпочтения строгие, это можно сделать, не нарушив относительного расположения пар  и
и 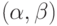 :
:
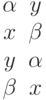
Тогда, по принципу единогласия,  и
и  , если они не равны. По транзитивности,
, если они не равны. По транзитивности,  . Теперь мы можем поменять
. Теперь мы можем поменять  и
и 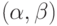 местами и в итоге получить, по свойству попарной независимости, что
местами и в итоге получить, по свойству попарной независимости, что  в исходном профиле. Вот и все, лемма доказана.
в исходном профиле. Вот и все, лемма доказана.
Третье доказательство теоремы 6.1. Третье доказательство, опирающееся на лемму 6.1, будет совсем коротким. Рассмотрим два исхода  и начнем с
и начнем с 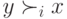 для всех
для всех  .i Пусть теперь, начиная с
.i Пусть теперь, начиная с 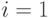 , каждый агент по очереди перемещает
, каждый агент по очереди перемещает  наверх
наверх  . По единогласию и лемме 6.1, будет существовать агент
. По единогласию и лемме 6.1, будет существовать агент  , при изменении предпочтения которого
, при изменении предпочтения которого  перемещается наверх относительно
перемещается наверх относительно  и после применения функции социального выбора. Докажем, что
и после применения функции социального выбора. Докажем, что  — диктатор. Рассмотрим произвольную пару исходов
— диктатор. Рассмотрим произвольную пару исходов 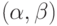 , для которой
, для которой 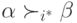 . Пусть ранжирование этой пары у других агентов будет совершенно произвольным.
. Пусть ранжирование этой пары у других агентов будет совершенно произвольным.
Рассмотрим теперь третий исход  и переместим
и переместим  выше всех остальных исходов для агентов от
выше всех остальных исходов для агентов от  до
до 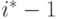 , ниже всех остальных для агентов от
, ниже всех остальных для агентов от 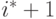 до
до  , а для самого
, а для самого  поместим
поместим  между
между  и
и  :
: 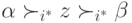 . Тогда, по попарной независимости и лемме 6.1, в предпочтениях социальной функции
. Тогда, по попарной независимости и лемме 6.1, в предпочтениях социальной функции  и
и  , а это значит, по транзитивности, что
, а это значит, по транзитивности, что  . Следовательно,
. Следовательно,  оказался диктатором.
оказался диктатором.
