|
поддерживаю выше заданые вопросы
|
Архитектурные аспекты параллелизма
Закон Амдала
Любая параллельная программа содержит последовательную часть. Это
ввод/вывод, менеджмент потоков, точки синхронизации и т.п. Обозначим долю
последовательной части за  . Тогда доля параллельной части будет
. Тогда доля параллельной части будет 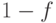 . В 1967 году Амдал рассмотрел ускорение такой программы на
. В 1967 году Амдал рассмотрел ускорение такой программы на  процессорах, исходя из
предположения линейного ускорения параллельной части:
процессорах, исходя из
предположения линейного ускорения параллельной части:
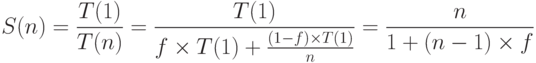
При неограниченном числе процессоров ускорение составит всего лишь 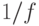 .
.
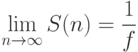
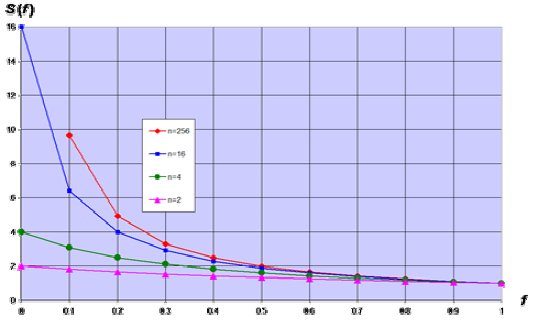
Так, например, если доля последовательной части 20%, то теоретически
невозможно получить ускорение вычислений более чем в пять раз! Таким образом,
превалирующую роль играет доля  , а вовсе не число процессоров!
, а вовсе не число процессоров!
Еще пример. Возможно ли ускорение вычислений в два раза при переходе с
однопроцессорной машины на четырехпроцессорную? Правильный ответ – не всегда,
так как все зависит от доли  .
.
По графикам  можно увидеть, что при
можно увидеть, что при 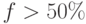 ни о каком существенном
ускорении говорить не приходится. Только если доля
ни о каком существенном
ускорении говорить не приходится. Только если доля  мала, многократное увеличение
числа процессоров становится экономически целесообразным.
мала, многократное увеличение
числа процессоров становится экономически целесообразным.
Более того, имея такую пессимистичную картину в теоретическом плане, на практике не избежать накладных расходов на поддержку многопоточных вычислений, состоящих из алгоритмических издержек (менеджмент потоков и т.п.), коммуникационных издержек на передачу информации между потоками и издержек в виде дисбаланса загрузки процессоров.
Дисбаланс загрузки процессоров возникает, даже если удалось разбить исходную задачу на равные по сложности подзадачи, так как время их выполнения может существенно различаться по самым разным причинам (от конфликтов в конвейере до планировщика ОС). В точках синхронизации (хотя бы в точке завершения всей задачи) потоки вынуждены ожидать наиболее долго выполняемых, что приводит к простою значительной части процессоров.
Закон Густафсона
Оптимистичный взгляд на закон Амдала дает закон Густафсона-Барсиса. Вместо
вопроса об ускорении на n процессорах рассмотрим вопрос о замедлении вычислений
при переходе на один процессор. Аналогично за  примем долю последовательной
части программы. Тогда получим закон масштабируемого ускорения:
примем долю последовательной
части программы. Тогда получим закон масштабируемого ускорения:
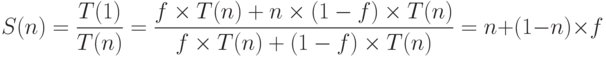
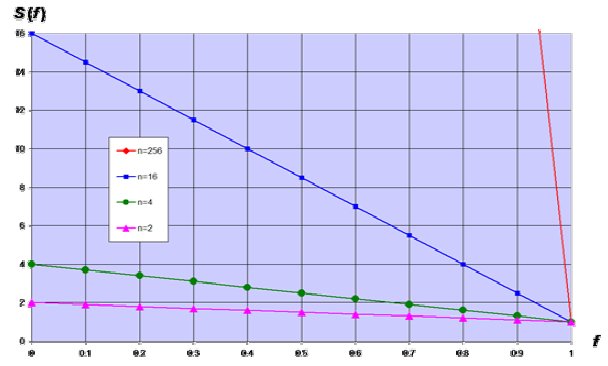
Теперь графики  демонстрируют совершенно иную картину: линейное
ускорение в зависимости от числа процессоров. Т.е. законы Амдала и Густафсона в
идентичных условиях дают различные значения ускорения. Где же ошибка? Каковы
области применения этих законов?
демонстрируют совершенно иную картину: линейное
ускорение в зависимости от числа процессоров. Т.е. законы Амдала и Густафсона в
идентичных условиях дают различные значения ускорения. Где же ошибка? Каковы
области применения этих законов?
Густафсон заметил, что, работая на многопроцессорных системах, пользователи склонны к изменению тактики решения задачи. Теперь снижение общего времени исполнения программы уступает объему решаемой задачи. Такое изменение цели обусловливает переход от закона Амдала к закону Густафсона.
Например, на 100 процессорах программа выполняется 20 минут. При переходе на систему с 1000 процессорами можно достичь времени исполнения порядка двух минут. Однако для получения большей точности решения имеет смысл увеличить на порядок объем решаемой задачи (например, решить систему уравнений в частных производных на более тонкой сетке). Т.е. при сохранении общего времени исполнения пользователи стремятся получить более точный результат.
Увеличение объема решаемой задачи приводит к увеличению доли параллельной части, так как последовательная часть (ввод/вывод, менеджмент потоков, точки синхронизации и т.п.) не изменяется. Таким образом, уменьшение доли f приводит к перспективным значениям ускорения.
Классификации архитектур ВС
Известно более десятка различных классификаций вычислительных систем [4]. Однако ключевой является классификация Флинна, на базе которой возникли новые классификации, детализирующие ее исходные классы.
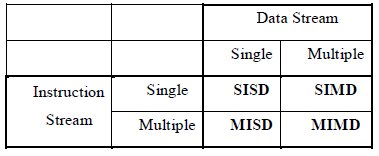
В 1966 году Флинн предложил рассматривать и потоки команд, и потоки данных либо как одиночные, либо как множественные. Так появились четыре класса вычислительных систем: SISD, MISD, SIMD, MIMD.
Классические фон-неймановские машины попадают в тривиальный класс SISD, в котором одиночный поток инструкций обрабатывает одиночный поток данных. Классические языки высокого уровня (такие, как C++) также ориентированы на программирование в классе SISD. В настоящее время выпуск SISD процессоров почти прекращен из-за их низкой производительности, которая обусловлена низким уровнем параллелизма вычислений (используется только мелкозернистый параллелизм).
Класс MISD, в котором множественный поток инструкций обрабатывает одиночный поток данных, пуст (бессмысленен).
Все современные передовые процессоры, как общего, так и специального назначения, попадают в класс MIMD. Они одновременно исполняют сразу несколько независимых потоков инструкций, аппаратно обеспечивая крупнозернистый параллелизм. Изъян классификации Флинна заключается в неразличимости современных направлений процессоростроения, что привело к возникновению множества новых классификаций.
Чистых представителей класса SIMD совсем немного. Класс ориентирован на выполнение программ, для которых характерна обработка больших регулярных массивов чисел. Здесь одиночный поток инструкций обрабатывает множественный поток данных. Именно представители класса SIMD впервые достигли производительности порядка GFLOPS.
Наиболее популярная идея класса SIMD – векторное процессирование. Векторный процессор поддерживает обработку не только скалярных, но и векторных операндов. Эффективное декодирование инструкций и удобные данные сказываются на производительности крайне позитивно. Поэтому векторную обработку внедряют и в процессоры классов SISD и MIMD. Например, SIMD расширение IA32 – технологии MMX и SSE.
Другим примером инкапсуляции техники SIMD является процессор STI Cell (альянс Sony, Toshiba и IBM). Процессор является гибридным объединением ведущего процессора (Power Processor Element, PPE) и восьми векторных сопроцессоров (Synergistic Processor Element, SPE). В качестве ведущего процессора используется 64- битный 2-поточный RISC процессор от IBM, традиционно включающий векторное расширение (Vector Multimedia eXtensions, AltiVec). SPE представляют собой параллельно работающие 128-битные SIMD процессоры.
Класс SIMD
Основные представители класса SIMD: векторные процессоры, матричные процессоры и процессоры с архитектурой VLIW.
У матричных процессоров нет аналогии с векторными. Матричный процессор – это массив процессоров с единым потоком команд. Большой исходный массив данных разделяют на части, подлежащие идентичной обработке. Каждый процессор массива обрабатывает соответствующую часть данных, выполняя единый поток инструкций.
Перспективным представителем класса SIMD является архитектура VLIW (очень длинное командное слово). Одна инструкция в такой системе команд представляет собой кортеж из нескольких RISC инструкций, которые независимы по данным между собой. VLIW процессору не нужно проверять инструкции кортежа на выявление структурных зависимостей, зависимостей по данным или по управлению. Теперь эти функции возложены на компилятор. Процессор сразу может переходить к фазе исполнения. Такие блоки, как динамический планировщик, станции резервации и т.д., здесь упразднены. Высвободившиеся ресурсы (транзисторы) перераспределяются для повышения производительности системы (увеличиваются размеры кешей, буферов BTB и TLB). Таким образом, процессор и компилятор обеспечивают хороший уровень параллелизма команд. Один из самых мощных VLIW процессоров – Intel Itanium 2.