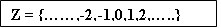|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Модульная арифметика
Криптография базируется на некоторых специфических областях математики, включая теорию чисел, линейную алгебру и алгебраические структуры. В этой лекции мы обсуждаем только те темы в вышеупомянутых областях, которые необходимы для понимания содержания следующих нескольких лекций. Читатели, которые знакомы с этими темами, могут пропустить лекцию полностью или частично. Подобные теоретические лекции встречаются всюду в этом курсе, когда это необходимо. Доказательства теорем и алгоритмов пропущены и даны только в приложении. Заинтересованный читатель может найти их в приложении Q.
2.1. Арифметика целых чисел
В арифметике целых чисел мы используем множество целых чисел и несколько операций. Вы знакомы с этим множеством и соответствующими операциями, но они рассмотрены здесь, чтобы объяснить потом основы действий со сравнениями по модулю m.
Множество целых чисел
Множество целых чисел, обозначенных Z, содержит все числа (без дробей) от минус бесконечности до плюс бесконечности (рис. 2.1).
Бинарные операции
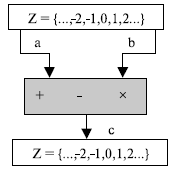
В криптографии нас интересует три бинарных операции в приложении к множеству целых чисел. Бинарные операции имеют два входа и один выход. Для целых чисел определены три общих бинарных операции — сложение, вычитание и умножение. Каждая из этих операций имеет два входа ( a и b ) и выход ( c ), как это показано на рис. 2.2. Два входа принимают числа из множества целых чисел; выход выводит результат операции — число из множества целых чисел.
Обращаем внимание, что деление не относится к этой категории операций, потому что мы скоро убедимся, что этой операции нужны два выхода вместо одного.
Пример 2.1
Следующие примеры показывают результаты трех бинарных операций на множестве двух целых чисел. Поскольку каждый вход может быть или положителен или отрицателен, мы имеем четыре случая для каждой операции.
Сложение 5+9=14 (-5)+9=4 5+(-9)=-4 (-5)+(-9)=-14 Вычитание 5-9=-4 (-5)-9=-14 5 - (-9)=14 (-5)- (-9)=+4 Умножение 5 x 9=45 (-5) x 9=-45 5 x (-9)=-45 (-5) x (-9)=45
Деление целых чисел
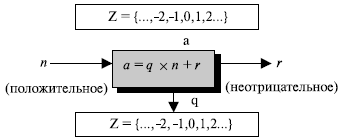
В арифметике целых чисел, если мы a делим на n, мы можем получить q и r. Отношения между этими четырьмя целыми числами можно показать как

В этом равенстве a называется делимое ; q — частное ; n — делитель и r — остаток. Обратите внимание, что это — не операция, поскольку результат деления a на n — это два целых числа, q и r. Мы будем называть это уравнением деления.
Пример 2.2
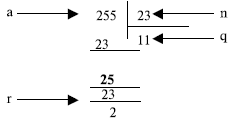
Предположим, что a = 255, а n = 23. Мы можем найти q = 11 и r = 2, используя алгоритм деления, мы знаем из элементарной арифметики — оно определяется, как показано на рис. 2.3.
Большинство компьютерных языков может найти частное и остаток, используя заданные языком операторы. Например, на языке C оператор "/" может найти частное, а оператор "%" — остаток.
Два ограничения
Когда мы используем вышеупомянутое уравнение деления в криптографии, мы налагаем два ограничения. Первое требование: чтобы делитель был положительным целым числом ( n > 0 ). Второе требование: чтобы остаток был неотрицательным целым числом ( r >= 0 ). Рисунок 2.4 показывает эти требования с двумя указанными ограничениями.
Пример 2.3
Предположим, мы используем компьютер или калькулятор, а r и q отрицательны, при отрицательном a. Как можно сделать, чтобы выполнялось ограничение, что число r должно быть положительным? Решение простое: мы уменьшаем значение q на 1 и добавляем значение n к r, чтобы r стало положительным.
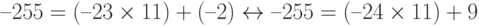
Мы уменьшили ( –23 ), получили ( –24 ) и добавили 11 к ( –2 ), чтобы получить + 9. Полученное равенство эквивалентно исходному.
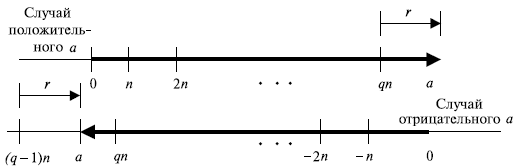
Граф уравнения деления
Мы можем изобразить рассмотренные выше уравнения с двумя ограничениями на n и r на рис. 2.5 с помощью двух графов. Первый показывает случай, когда число a положительно; второй — когда отрицательно.
Граф начинается с нуля и показывает, как мы можем достигнуть точки, представляющей целое число a на линии. В случае положительного a мы должны перемещаться на величину  направо и затем добавить дополнительную величину r в том же самом направлении. В случае отрицательного a мы должны двигаться на величину
направо и затем добавить дополнительную величину r в том же самом направлении. В случае отрицательного a мы должны двигаться на величину 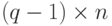 налево (число q в этом случае отрицательно) и затем дополнять число r в противоположном для указанного выше движения направлении. В обоих случаях значение r положительно.
налево (число q в этом случае отрицательно) и затем дополнять число r в противоположном для указанного выше движения направлении. В обоих случаях значение r положительно.