Организационный инструментарий менеджмента

Аналитические параметры сетевых графиков

Сетевые графики представляют собой графо-аналитические организационные инструменты. Рассмотрев графическую часть этих инструментов, перейдем к рассмотрению аналитических параметров. Аналитические параметры сетевых графиков представлены в табл. 4.4.

Таблица 4.4. Аналитические параметры сетевых графиков

№ п/п	Название параметра	Условное обозначение
1	Код начального события работы	i-j
2	Код начального события работы	i
3	Код конечного события работы	j
4	Код предшествующей работы	h-i
5	Код события, предшествующего работе h-j	h
6	Код работы, последующей за конечным событием работы	j-k
7	Код события, последующего работе j-k	k
8	Путь	L
9	Продолжительность пути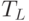
10	Критический путь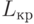
11	Продолжительность критического пути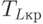
12	Продолжительность работы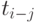
13	Раннее начало работы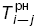
14	Раннее окончание работы
15	Позднее начало работы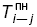
16	Позднее окончание работы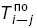
17	Общий (полный) резерв времени работы
18	Частный (свободный) резерв времени работы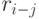
19	Резерв времени пути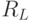

Прежде всего, определяются ранние сроки начала (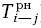) и окончания (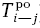) каждой работы. Далее - поздние сроки начала (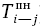) и окончания () каждой работы. Затем определяются критические работы, а для некритических работ - резервы времени (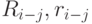). И наконец, определяется так называемый коэффициент напряженности каждой работы ().

Ранние сроки начала и окончания работ сетевого графика определяют последовательно, слева направо по графику, от исходного события сети к завершающему.

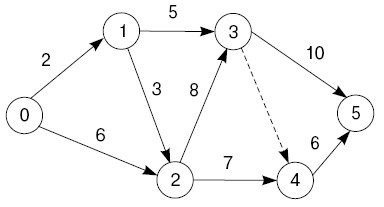
Произведем расчет графика, изображенного на рис. 4.11.

Рис. 4.11. Пример сетевого графика

Для всех работ, выходящих из исходного события сети, раннее начало всегда равно нулю, т.е.

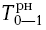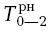= 0; = 0

Для всех последующих работ, прежде чем определить величину раннего начала, необходимо знать раннее окончание работ, выходящих из исходного события сети. Эта величина для всех работ сетевого графика будет равна сумме раннего начала работы и ее продолжительности, т.е. в общем виде:

(1)

Для работ 0-1 и 0-2 ранние окончания будут равны 2 и 6 дней соответственно:

= 0 + 2 = 2,

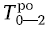= 0 + 6 = 6.

Если раннее окончание работы 0-1 равно 2, то могут ли работы 1-2 и 1-3 начинаться раньше, чем закончится работа 0-1? Очевидно, нет. Все работы, следующие за работой 0-1, могут начинаться только после самого раннего окончания работы 0-1, т.е. эта величина и есть раннее начало работ 1-2 и 1-3:

Другими словами, раннее начало данной работы равно раннему окончанию предшествующей работы. Пользуясь этим правилом, определим раннее начало работы 1-2 и 1-3.

Какая выявляется закономерность? Работы, выходящие из исходного события, имеют одно и то же раннее начало, равное нулю. Работы, выходящие из события № 1, тоже имеют одно и то же раннее начало - 2. Очевидно, все работы, которые выходят из одного и того же события, всегда имеют одну и ту же величину раннего начала.

Определив раннее начало для одной работы, мы можем записать его значение абсолютно для всех работ, выходящих из этого же события.

Используя формулу (1), определим раннее окончание работ 1-2 и 1-3.

Раннее окончание работы 1-2 будет равно раннему началу работы 1-2 (2 дня) плюс продолжительность этой работы (3 дня), т.е. 2 + 3 равно 5, и раннее окончание работы 1-3 будет равно раннее начало работы 1-3 (2 дня) плюс продолжительность этой работы (5 дней), т.е. 2 + 5 равно 7.

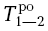= 2 + 3 = 5,

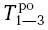= 2 + 5 = 7

Далее определим раннее начало работы 2-3 и 2-4. Здесь важно напомнить, что сложное событие совершается только тогда, когда все работы, в том числе и самая длительная, завершаются. Для работы 2-3 предшествующими работами являются 1-2 и 0-2, которые имеют ранние окончания соответственно 5 и 6. И раннее начало работы 2-3 будет определяться наибольшим ранним окончанием предшествующих работ. В виде формулы это можно записать так:

(2)

т.е. раннее начало данной работы равно максимальному раннему окончанию непосредственно предшествующих ей работ.

Используя формулы (1) и (2), определим раннее начало и окончание для всех остальных работ сетевого графика.

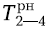= 6 (точно так же, как и у работы 2-3)

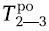= 6 + 8 = 14, 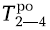= 6 + 7 = 13;

= max [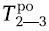; 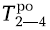] = 14.

Напомним, что логическая зависимость является полноправным элементом расчета параметров сети.

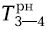= 14 (точно так же, как и у работы 3-5)

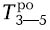= 14 + 10 = 24, 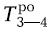= 14 + 0 = 14;

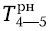= max [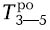; 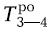] = 14;

= 14 + 6 = 20.

Поздние сроки начала и окончания каждой работы в отличие от ранних сроков определяются в обратном порядке - от завершающего события графика к исходному, т.е. справа налево по графику.

Вернемся к сетевому графику на рис. 4.11. В предыдущем пункте было установлено, что самое раннее окончание работы 3-5 равно 24, а 4-5 равно 20. А чему равно самое позднее окончание этих работ? Очевидно, 24 дня, так как позже этого срока не должна заканчиваться ни одна работа.

Действительно, у работы 3-5 как раннее окончание, так и позднее окончание равны 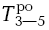24:

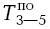= 24

= 24

У работы 4-5 самое раннее окончание - 19, а самое позднее - 24.

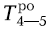= 19

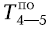= 24

А чему будут равны поздние начала этих работ? Очевидно, необходимо начинать эти работы в такой момент, чтобы успеть уложиться в заданную для данной работы продолжительность и закончить ее в самый поздний срок ее окончания. Например, работу 3-5 мы не можем начать на 15-й день, ибо мы не уложимся в самые поздние сроки ее окончания (15 + 10 = 25). Следовательно,

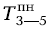= 24 - 10 = 14; а 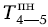= 24 - 6 = 18

Таким образом, позднее начало данной работы равно ее позднему окончанию за вычетом ее продолжительности:

(3)

А чему будет равно позднее окончание работ 3-4 и 2-4? Эти работы мы должны закончить с таким расчетом, чтобы успеть начать в самое позднее время следующую работу 4-5, если же работы 3-4 или 2-4 закончим самое позднее через 19 дней, то самое позднее начало следующей работы будет также 19 дней, а мы определили, что 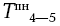 = 18. Таким образом, позднее окончание предшествующих работ должно всегда равняться самому позднему началу следующих. Отсюда

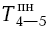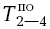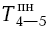= = 18

= = 18

Как видим, работы, входящие в пятое событие, имеют одну и ту же величину 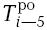 = 24 и работы, входящие в четвертое событие, имеют также одну и ту же величину  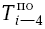= 18. Следовательно, определив для одной из работ величину  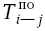мы автоматически записываем эту же величину для всех других работ, входящих в это же событие.

Далее определим позднее начало работ 2-3 и 3-4 (3):

= 18 - 7 = 11,

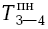= 18 - 0 = 18.

А чему будет равно время позднего окончания работ 2-3 и 1-3? Ведь из третьего события выходят две работы (3-5 и 3-1). Какое позднее начало принять в качестве позднего окончания работы 2-3 и 1-3? Работа 3-5 имеет 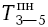= 14, а работа 3-1 имеет = 18. Совершенно очевидно, что в качестве 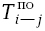 следует принимать минимальное  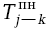(т.е. следующей работы). Если же мы поступим наоборот и возьмем в данном случае  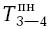= = 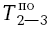18, то получится, что работа 3-5 будет закончена: 18 + 10 = 28, а это нас не удовлетворяет, так как общая продолжительность работ по графику 24 дня.

Следовательно, позднее окончание данной работы всегда равно минимальному позднему началу непосредственно следующих за ней работ, т.е.:

(4)

Используя формулы (3) и (4), определим поздние сроки для всех остальных работ.

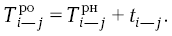
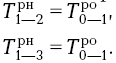
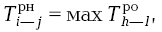
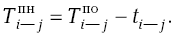
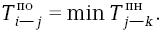
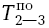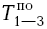= 14,

= 14;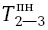

= 14 - 8 = 6,

= 14 - 5 = 9;

= 6,

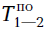= 6;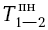

= 6 - 3 = 3,

= 6 - 6 = 0;

= 3,

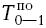= 3 - 2 = 1.