|
Мне нужно изучить математическую статистику с нуля для обработки данных на компьютере. Читаю уже вторую лекцию, но пока ничего даже отдалённо близкого к моей цели не нахожу. Есть ли математическая статистика в дальнейших лекциях? Или я зря теряю время на изучение этого курса? У меня крайне ограниченный временной срок - я не могу терять время на самостоятельную проверку моего вопроса посредством изучения данного курса. |
Статистическое изучение взаимосвязей между социально-экономическими явлениями
12.1. Понятие о функциональной и корреляционной связи
Между общественными и экономическими явлениями имеется два основных типа связи - функциональная и статистическая (называемая также стохастической, вероятностной или корреляционной). Перед тем как рассмотреть их подробнее, введем понятия независимых и зависимых признаков.
Независимыми, или факторными, называют признаки, которые вызывают изменения других, связанных с ними признаков. Признаки, изменение которых под воздействием определенных факторов требуется проследить, называют зависимыми, или результативными.
При функциональной связи изменение независимых переменных приводит к получению точно определенных значений зависимой переменной.
Наиболее часто функциональные связи проявляются в естественных науках, например в механике функциональной является зависимость расстояния, пройденного объектом, от скорости его движения и т. п.
При статистической связи каждому значению независимой переменной Х соответствует множество значений зависимой переменной Y, причем не известно заранее, какое именно. Например, мы знаем, что прибыль коммерческого банка определенным образом связана с размером его уставного капитала (этот факт не подлежит сомнению). Тем не менее, нельзя вычислить точную величину прибыли при заданном значении последнего показателя, так как она зависит еще и от множества других факторов, помимо размера уставного капитала, среди которых имеются и случайные. В нашем случае, скорее всего, мы определим лишь среднее значение прибыли, которое будет получено в целом по совокупности банков со сходным объемом уставного капитала. Таким образом, статистическая связь отличается от функциональной наличием действия на зависимую переменную большого числа факторов.
Заметим, что статистическая связь проявляется лишь "в общем и среднем" при большом числе наблюдений за явлением. Так, интуитивно мы можем предполагать, что существует зависимость между объемом основных фондов предприятия и получаемой им прибылью, а именно с увеличением первого размер прибыли возрастает. Но на это можно возразить и привести пример предприятия, обладающего достаточным количеством современного производственного оборудования, но тем не менее терпящего убытки. В данном случае мы имеем наглядный пример статистической связи, которая проявляется лишь в больших совокупностях, содержащих десятки и сотни единиц в отличие от функциональной, подтверждающейся для каждого наблюдения.
Корреляционной является статистическая связь между признаками, при которой изменение значений независимой переменной Х приводит к закономерному изменению математического ожидания случайной величины Y.
Пример 12.1. Предположим, что имеются данные по предприятиям о размере нераспределенной прибыли предыдущего года, объеме инвестиций в основной капитал и о суммах, выделенных на приобретение ценных бумаг (тыс. ден. ед.):
| Номер предприятия | Нераспределенная прибыль предыдущего года | Приобретение ценных бумаг | Инвестиции в основные фонды |
|---|---|---|---|
| 1 | 3 010 | 190 | 100 |
| 2 | 3 100 | 182 | 250 |
| 3 | 3 452 | 185 | 280 |
| 4 | 3 740 | 170 | 270 |
| 5 | 3 980 | 172 | 330 |
| 6 | 4 200 | 160 | 420 |
| 7 | 4 500 | 145 | 606 |
| 8 | 5 020 | 120 | 690 |
| 9 | 5 112 | 90 | 800 |
| 10 | 5 300 | 30 | 950 |
Из таблицы видно, что имеется прямое соответствие между нераспределенной прибылью предприятия и его инвестициями в основной капитал: при увеличении нераспределенной прибыли объем инвестиций также возрастает. Теперь обратим внимание на связь между показателем нераспределенной прибыли и объемом приобретенных ценных бумаг. Здесь она носит совершенно иной характер: увеличение первого показателя приводит к прямо противоположному эффекту - стоимость приобретенных ценных бумаг за редким исключением (что уже однозначно исключает наличие функциональной связи) уменьшается. Такой визуальный анализ данных, при котором наблюдения ранжируются по возрастанию или убыванию независимой величины х, а затем анализируется изменение значений зависимой величины у, называется методом приведения параллельных данных.
В рассмотренном примере в первом случае связь прямая, т.д. увеличение (уменьшение) одного показателя влечет увеличение (уменьшение) другого (наблюдается соответствие в изменениях показателей), а во втором - обратная, т.д. уменьшение одного показателя вызывает рост другого или же увеличение одного соответствует снижению другого.
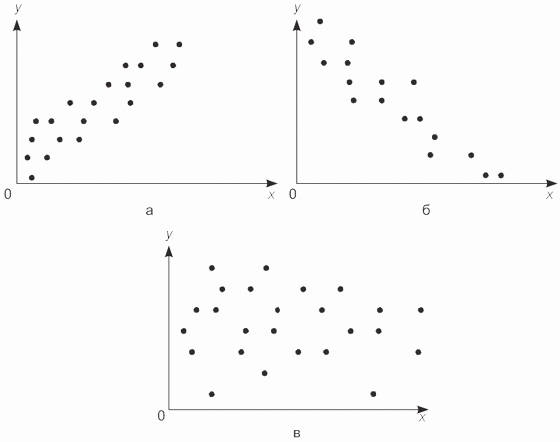
Прямая и обратная зависимости характеризуют направление связи между признаками, которую можно проиллюстрировать графически с помощью поля корреляции. При его построении в прямоугольной системе координат на оси абсцисс располагают значения независимой переменной х, а на оси ординат - зависимой у. Пересечение координат обозначают точками, которые символизируют наблюдения. По форме рассеяния точек на корреляционном поле судят о форме и тесноте связи. На рисунке 12.1 приводятся корреляционные поля, соответствующие различным формам связи.
а - прямая (положительная) связь;
б - обратная (отрицательная) связь;
в - отсутствие связи
Раздел статистической науки, занимающийся исследованием причинных связей между социально-экономическими явлениями и процессами, имеющими количественное выражение, - это корреляционно-регрессионный анализ. По существу имеются два отдельных направления анализа - корреляционный и регрессионный. Однако в связи с тем, что на практике они применяются чаще всего комплексно (исходя из результатов корреляционного анализа проводят регрессионный), их объединяют в один вид.
Проведение корреляционно-регрессионного анализа предполагает решение следующих задач:
- выявление из большого числа факторов наиболее информативных, оказывающих более существенное воздействие на результативную величину (предварительный анализ, базирующийся на простейших методах выявления зависимостей и экспертных оценках);
- определение направления и количественной оценки тесноты зависимости между факторной величиной Х и результативной Y (при этом факторных переменных может быть достаточно много, тогда определяется множественная корреляция);
- нахождение математической функции, описывающей зависимость результативного показателя Y от наиболее информативных факторных Х. Эта функция выполняет роль модели, которая аналитически выражает зависимость условного среднего значения результативного признака от факторных переменных
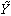 = f(x1.x3....xk).
= f(x1.x3....xk). - оценка качества полученной модели, определение возможной величины ошибки получаемых по этой модели прогнозных значений Y;
- построение прогнозов.
Из перечисленных задач первые две относят непосредственно к задачам корреляционного анализа, три последующие - к регрессионному анализу и только по отношению к количественным показателям.
12.1.1. Требования к статистической информации, исследуемой методами корреляционно-регрессионного анализа
Методы корреляционно-регрессионного анализа можно применить не ко всем статистическим данным. Перечислим основные требования, предъявляемые к анализируемой информации:
- используемые для исследования наблюдения должны являться случайно выбранными из генеральной совокупности объектов. В противном случае исходные данные, представляющие собой определенную выборку из генеральной совокупности, не будут отражать ее характер, полученные по ним выводы о закономерностях развития окажутся бессмысленными и не имеющими никакой практической ценности;
- требование независимости наблюдений друг от друга. Зависимость наблюдений друг от друга называется автокорреляцией, для ее устранения в теории корреляционно-регрессионного анализа созданы специальные методы;
- исходная совокупность данных должна быть однородной, без аномальных наблюдений. И действительно, одно-единственное, резко выделяющееся наблюдение может привести к катастрофическим последствиям для регрессионной модели, ее параметры окажутся смещенными, выводы абсурдными;
- желательно, чтобы исходные данные для анализа подчинялись нормальному закону распределения. Нормальный закон распределения используется для того, чтобы при проверке значимости коэффициентов корреляции и построении для них интервальных границ можно было использовать определенные критерии. Если же проверять значимость и строить интервальные оценки не требуется, переменные могут иметь любой закон распределения. В регрессионном анализе при построении уравнения регрессии требование нормальности распределения исходных данных предъявляется лишь к результативной переменной Y, независимые факторы рассматриваются как неслучайные величины и могут в действительности иметь любой закон распределения. Как и в случае корреляционного анализа, требование нормальности распределения нужно для проверки значимости регрессионного уравнения, его коэффициентов и нахождения доверительных интервалов;
- число наблюдений, по которым устанавливается взаимосвязь признаков и строится модель регрессии, должно превышать количество факторных признаков хотя бы в 3-4 раза (а лучше в 8-10 раз). Как отмечалось выше, статистическая связь проявляется только при значительном числе наблюдений на основе действия закона больших чисел, причем, чем связь слабее, тем больше требуется наблюдений для установления связи, чем сильнее - тем меньше;
- факторные признаки Х не должны находиться между собой в функциональной зависимости. Значительная связь независимых (факторных, объясняющих) признаков между собой указывает на мультиколлениарность. Ее наличие приводит к построению неустойчивых регрессионных моделей, "ложных" регрессий.
12.1.2. Линейная и нелинейная связи
Линейная связь выражается прямой линией, а нелинейная - какой-либо кривой линией. Линейная связь выражается уравнением прямой: y = a0 + ai*x. Прямая наиболее привлекательна с точки зрения простоты расчета параметров уравнения. К ней прибегают всегда, в том числе и в случаях нелинейных связей, когда нет угрозы значительных потерь в точности оценок. Однако для некоторых зависимостей представление их в линейной форме приводит к большим ошибкам (ошибкам аппроксимации) и, как следствие, к ложным выводам. В этих случаях используют нелинейные регрессионные функции, которые в общем случае могут иметь любой произвольный вид, тем более что современное программное обеспечение позволяет быстро их построить. Чаще всего для выражения нелинейной связи используются следующие нелинейные уравнения: степенное, параболическое, гиперболическое, логарифмическое.
Параметры этих моделей, как и в случаях линейных зависимостей, оцениваются также на основе метода наименьших квадратов (см. п. 12.3.1).
12.2. Корреляционно-регрессионный анализ
Основными задачами корреляционного анализа являются определение наличия связи между отобранными признаками, установление ее направления и количественная оценка тесноты связи. Для этого в корреляционном анализе сначала оценивается матрица парных коэффициентов корреляции, затем на ее основе определяются частные и множественные коэффициенты корреляции и детерминации. После нахождения значений коэффициентов проверяют их значимость. Конечный результат корреляционного анализа - это отбор факторных признаков Х для дальнейшего построения уравнения регрессии, позволяющего количественно описать взаимосвязь.
Рассмотрим этапы корреляционного анализа подробнее.
12.2.1. Парные (линейные) коэффициенты корреляции
Корреляционный анализ начинается с расчета парных (линейных) коэффициентов корреляции.
Парный коэффициент корреляции представляет собой меру линейной зависимости между двумя переменными на фоне действия остальных переменных, входящих в модель.
В зависимости от того, какой порядок вычислений более удобен исследователю, расчет данного коэффициента проводят по одной из следующих формул:
-
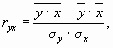
где у - среднее арифметическое значение у;
х - среднее арифметическое значение х;
ух - среднее арифметическое значение из произведений у и х;
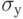 - среднеквадратическое отклонение признака у;
- среднеквадратическое отклонение признака у;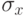 - среднеквадратическое отклонение признака х.
- среднеквадратическое отклонение признака х. -

-

- если известны суммы переменных у и х, используют следующие модификации формул:

или

Парный коэффициент корреляции изменяется в пределах от -1 до +1. Абсолютное значение, равное единице, свидетельствует о том, что связь функциональная: -1 - обратная (отрицательная), +1 - прямая (положительная). Нулевое значение коэффициента указывает на отсутствие линейной связи между признаками.
Качественную оценку полученным количественным значениям парных коэффициентов корреляции можно дать на основе шкалы, представленной в табл. 12.2.
| Значение коэффициента корреляции (по модулю) | Качественная характеристика силы связи |
|---|---|
| До 0,3 | Практически отсутствует (слабая) |
| 0,3-0,7 | Средняя |
| 0,7-0,9 | Высокая |
| 0,9-0,99 | Весьма высокая |
Примечание: положительное значение коэффициента говорит о том, что связь между признаками прямая, отрицательное - обратная.
12.2.2. Оценка существенности связи
После того, как значения коэффициентов получены, следует проверить их значимость. Поскольку исходные данные, по которым устанавливается взаимосвязь признаков, являются определенной выборкой из некоей генеральной совокупности объектов, исчисленные по этим данным парные коэффициенты корреляции будут выборочными. Таким образом, они лишь оценивают связь исходя из той информации, которую несут отобранные единицы наблюдения. Если исходные данные "хорошо" отражают структуру и закономерности генеральной совокупности, то и исчисленный по ним коэффициент корреляции будет показывать реальную связь, присущую в действительности всей исследуемой совокупности объектов. Если данные не "копируют" взаимосвязи совокупности в целом, то и рассчитанный коэффициент корреляции сформирует ложное представление о зависимости. В идеале, чтобы установить этот факт, требуется исчислить коэффициент корреляции на основе данных всей совокупности и сравнить его с исчисленным по отобранным наблюдениям. Однако на практике, как правило, этого сделать нельзя, так как зачастую неизвестна вся генеральная совокупность или же она слишком велика. Поэтому о том, насколько реально коэффициент представляет действительность, можно судить лишь приблизительно. На основе логики легко прийти к выводу, что, очевидно, с увеличением числа наблюдений (при 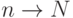 ) доверие к исчисленному коэффициенту будет увеличиваться.
) доверие к исчисленному коэффициенту будет увеличиваться.
Значимость парных коэффициентов корреляции проверяется одним из двух способов: с помощью таблицы Фишера - Йейтса или по t-критерию Стьюдента. Рассмотрим способ проверки с помощью таблицы Фишера - Йейтса как наиболее простой.
В начале проверки задается уровень значимости (чаще всего обозначаемый буквой греческого алфавита "альфа" -  ), который показывает вероятность принятия ошибочного решения. Возможность совершить ошибку вытекает из того факта, что для определения взаимосвязи используются данные не всей совокупности, а лишь ее части. Обычно
), который показывает вероятность принятия ошибочного решения. Возможность совершить ошибку вытекает из того факта, что для определения взаимосвязи используются данные не всей совокупности, а лишь ее части. Обычно  принимает следующие значения: 0,05; 0,02; 0,01; 0,001. Например, если
принимает следующие значения: 0,05; 0,02; 0,01; 0,001. Например, если  = 0,05, то это означает, что в среднем в пяти случаях из ста принятое решение о значимости (или незначимости) парных коэффициентов корреляции будет ошибочным; при
= 0,05, то это означает, что в среднем в пяти случаях из ста принятое решение о значимости (или незначимости) парных коэффициентов корреляции будет ошибочным; при  = 0,001 - в одном случае из тысячи и т.д.
= 0,001 - в одном случае из тысячи и т.д.
Вторым параметром при проверке значимости является число степеней свободы v, которое в данном случае вычисляется как v = n - 2. По таблице Фишера - Йейтса находится критическое значение коэффициента корреляции rкр. ( = 0,05, v = n - 2). Коэффициенты, значения которых по модулю больше найденного критического значения, считаются значимыми.
= 0,05, v = n - 2). Коэффициенты, значения которых по модулю больше найденного критического значения, считаются значимыми.
Пример 12.2. Предположим, что в первом случае имеется 12 наблюдений, и по ним вычислили парный коэффициент корреляции, который оказался равным 0,530, во втором - 92 наблюдения, и рассчитанный парный коэффициент корреляции составил 0,36. Но если мы проверим их значимость, в первом случае коэффициент окажется незначимым, а во втором - значимым, невзирая на то, что он по величине гораздо меньше. Оказывается, в первом случае слишком мало наблюдений, что повышает требования, и критическая величина парного коэффициента корреляции при уровне значимости  = 0,05 составляет 0,576 (v = 12 - 2), а во втором - наблюдений значительно больше и достаточно превысить критическое значение 0,205 (v = 92 - 2), чтобы коэффициент корреляции при том же уровне
= 0,05 составляет 0,576 (v = 12 - 2), а во втором - наблюдений значительно больше и достаточно превысить критическое значение 0,205 (v = 92 - 2), чтобы коэффициент корреляции при том же уровне  оказался значимым. Таким образом, чем меньше наблюдений, тем всегда будет выше критическое значение коэффициента.
оказался значимым. Таким образом, чем меньше наблюдений, тем всегда будет выше критическое значение коэффициента.
Проверка значимости по существу решает вопрос, случайны или нет полученные результаты расчетов.
12.2.3. Определение множественного коэффициента корреляции
Следующий этап корреляционного анализа связан с расчетом множественного (совокупного) коэффициента корреляции.
Множественный коэффициент корреляции характеризует тесноту линейной связи между одной переменной и совокупностью других переменных, рассматриваемых в корреляционном анализе.
Если изучается связь между результативным признаком y и лишь двумя факторными признаками х1 и х2, то для вычисления множественного коэффициента корреляции можно использовать следующую формулу, компонентами которой являются парные коэффициенты корреляции:
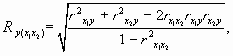
где r - парные коэффициенты корреляции.