|
Мне нужно изучить математическую статистику с нуля для обработки данных на компьютере. Читаю уже вторую лекцию, но пока ничего даже отдалённо близкого к моей цели не нахожу. Есть ли математическая статистика в дальнейших лекциях? Или я зря теряю время на изучение этого курса? У меня крайне ограниченный временной срок - я не могу терять время на самостоятельную проверку моего вопроса посредством изучения данного курса. |
Индексы в статистике
10.5. Анализ динамики среднего уровня показателя
На формирование среднего уровня качественного показателя оказывают влияние два фактора: во-первых, изменение индивидуальных значений самой индексируемой величины в отчетном периоде по сравнению с базисным, и, во-вторых, изменение структуры исследуемой совокупности (уменьшение или увеличение доли единиц с более низким или более высоким уровнем этого показателя). Например, на динамику средней цены влияют изменения индивидуальных уровней цен и различия в структуре продаж отчетного периода по сравнению с базисным; на формирование среднего уровня фондоотдачи - изменения фондоотдачи отдельных видов основных фондов и доли основных фондов с более высоким (низким) уровнем фондоотдачи в общей их совокупности (структурный фактор).
Относительное изменение среднего уровня качественного показателя характеризуется с помощью системы индексов переменного, постоянного состава и индекса структурных сдвигов, позволяющих оценить влияние каждого фактора на его динамику.
Покажем общую схему построения системы индексов, характеризующих динамику среднего уровня качественного показателя. Индекс переменного состава отражает изменение среднего уровня качественного показателя за счет двух факторов. Пусть х - индексируемая величина, f - вес индекса. В общем виде этот индекс рассчитывается как отношение среднего уровня показателя в отчетном периоде к среднему уровню показателя в базисном периоде. Индекс переменного состава для любых качественных показателей может быть записан следующим образом:

Индекс постоянного (фиксированного) состава показывает, как в среднем изменилось значение качественного показателя у единиц совокупности при одинаковой фиксированной ее структуре. В общем виде его можно записать следующим образом:
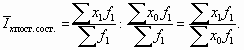
Формула индекса влияния структурных сдвигов, представляющего собой отношение средних величин рассматриваемого качественного показателя, рассчитанных при структуре совокупности отчетного и базисного периодов при базисном уровне качественного показателя, выглядит следующим образом:

Поскольку индекс переменного состава показывает изменение исследуемого явления за счет всех факторов, то между индексами существует следующая взаимосвязь:
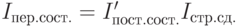 .
.
Так, при изучении изменения средней цены товара (например, продаваемого в разных регионах) индекс переменного состава можно записать следующим образом:
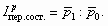
Подставляя вместо P0 и P1 выражения для расчета средних уровней цен товара отчетного и базисного периодов, получим его развернутую формулу
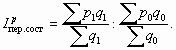
На его величину оказывают влияние два фактора: изменение цены товара в каждом регионе и структуры продаж. Абсолютное изменение среднего уровня цены товара за счет двух факторов покажет разность между числителем и знаменателем рассматриваемого индекса:

Индекс цен постоянного (фиксированного) состава показывает изменение средней цены товара только за счет изменений цен в каждом регионе. Индекс цен постоянного состава имеет вид
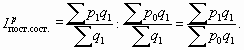
Абсолютное изменение среднего уровня цены за счет изменения индексируемой величины покажет разность между числителем и знаменателем данного индекса
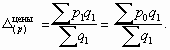
Индекс структурных сдвигов позволяет оценить влияние на формирование среднего уровня цены изменений в структуре продаж товара:

Абсолютное изменение среднего уровня качественного показателя (в данном случае средней цены) за счет структурных сдвигов

Пример 10.6. В таблице приведены цены и объемы продаж товара "А" в трех регионах.
| Регион | Цена товара "А", руб. за кг | Объем продаж товара "А", тыс. кг | ||
|---|---|---|---|---|
| базисный период, p0 | отчетный период, p1 | базисный период, q0 | отчетный период, q1 | |
| I | 61 | 69 | 550,0 | 520,7 |
| II | 58 | 65 | 420,4 | 380,5 |
| III | 53 | 57 | 711,8 | 603,4 |
Индекс цен переменного состава равен

Общее измерение средней цены в абсолютном выражении

За счет действия двух факторов средняя цена увеличилась на 11,1%, или на 6,31 руб.
Для определения влияния первого фактора (цен в каждом регионе) на динамику средней цены исчислим индекс цен постоянного состава:

Тогда влияние первого фактора в абсолютном выражении можно определить как

Таким образом, в результате изменения цен товара "А" в отдельных регионах его средняя цена увеличилась на 10,8%, или на 6,15 руб.
Влияние на анализируемый показатель структурных изменений в структуре продаж товара "А" покажет индекс структурных сдвигов
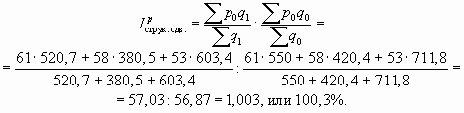
В абсолютном выражении
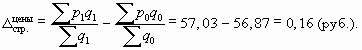
В результате изменения структуры продаж товаров по регионам средняя цена возросла на 0,3%, или 16 копеек.
Проверим взаимосвязь индексов и абсолютных приростов:

10.6. Факторный анализ
Как отмечалось выше, индексы используются не только для характеристики интенсивности изменения социально-экономических явлений, но и для выявления влияния на этот процесс различных факторов. Так, например, на основе индексов определяют степень влияния изменения себестоимости продукции и структуры производства на динамику затрат на производство продукции; производительности труда и затрат рабочего времени - на изменение объема продукции и т.д.
Покажем это по данным примера 10.2 о ценах и объеме продаж молочной продукции (см. табл. в примере).
Пример 10.7. Проанализируем прирост товарооборота под влиянием двух факторов: изменения цен на товары и объема их продаж. Общий индекс товарооборота равен

Товарооборот в относительном выражении увеличился на 16,3%. Найдем абсолютный прирост товарооборота за счет двух факторов - разность между числителем и знаменателем этого индекса:
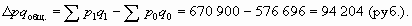
Как видим, товарооборот возрос на 94 204 руб. (или 16,3%) за счет двух факторов.
Общий индекс цен, как отмечалось выше, показывает относительное изменение товарооборота под влиянием цен:
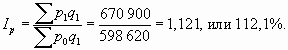
Разность между числителем и знаменателем этого индекса позволяет оценить влияние цен на динамику товарооборота в абсолютном выражении:
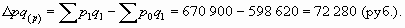
Таким образом, за счет роста цен на молочную продукцию товарооборот увеличился на 72 280 руб., или на 12,1%.
Общий индекс физического объема товарооборота отражает в относительном измерении влияние второго фактора - количества проданных товаров на динамику изучаемого показателя:
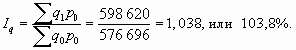
Абсолютный прирост товарооборота за счет изменения объема продаж молочной продукции определим как разность между числителем и знаменателем этого индекса
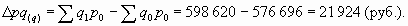
Произведение индексов цен и физического объема товарооборота равно общему индексу товарооборота:
lpq= lp x lq = 1,121 * 1,038 = 1,163 или 116,3%
Если сложить абсолютные изменения товарооборота за счет первого и второго фактора, то получим его общее абсолютное изменение:
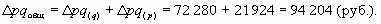
Аналогично проводится анализ изменения затрат на производство продукции под воздействием двух факторов: изменения себестоимости продукции и объемов производства. Относительное влияние отражают индексы
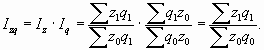
Абсолютное изменение затрат на производство за счет отдельных факторов рассчитывается следующим образом:
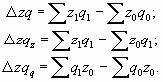
Взаимосвязь абсолютных изменений определяется уравнением

