|
По первому тесту выполнил дважды задания. Результат получается правильный (проверял калькулятором). Пишет, что "Задание не проверено" и предлагает повторить. |
Обработка матриц в Паскале
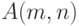 так, чтобы строки с нечётными индексами были упорядочены по убыванию, c чётными — по возрастанию.
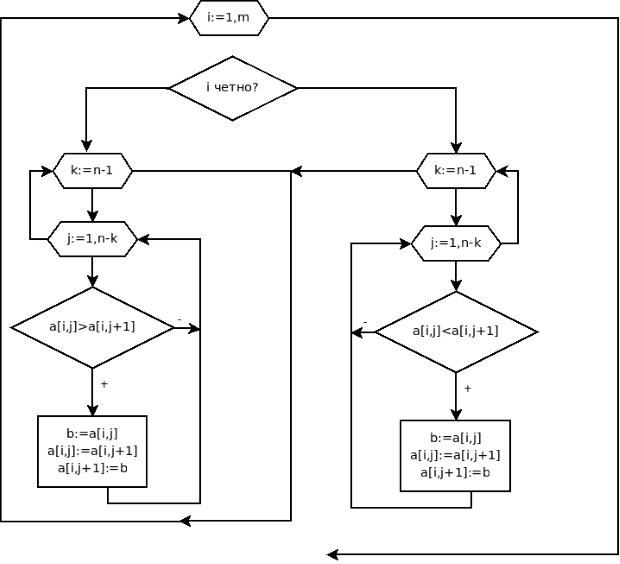
так, чтобы строки с нечётными индексами были упорядочены по убыванию, c чётными — по возрастанию.Каждая строка матрицы является одномерным массивом. Поэтому для упорядочения строки или столбца можно использовать обычные алгоритмы сортировки массивов. При решении задачи необходимо последовательно просматривать все строки матрицы, если номер строки нечётный, то сортируем строку методом пузырька по убыванию, иначе — по возрастанию. Блок-схема этого алгоритма представлена на рис. 6.25.
Ниже представлено консольное предложение для решения этой задачи с комментариями.
var a : array [ 1.. 15, 1.. 15 ] of real;
j, i, k,m, n : byte; b : real;
begin
//Ввод размеров матрицы.
writeln ( ’введите m и n ’ );
readln (m, n );
//Ввод матрицы.
writeln ( ’Матрица А ’ );
for i :=1 to m do
for j :=1 to n do
read ( a [ i, j ] );
//Преобразование матрицы.
for i :=1 to m do
if ( i mod 2)=0 then {Если номер строки четный, то}
begin {упорядочить ее элементы по возрастанию.}
{Упорядочение строки матрицы методом пузырька по возрастанию.}
for k:=1 to n-1 do
for j :=1 to n-k do
if a [ i, j ] > a [ i, j +1] then
begin
b:=a [ i, j ];
a [ i, j ] : = a [ i, j + 1 ];
a [ i, j +1]:=b;
end
end
else {Если номер строки нечетный, то упорядочить ее элементы по}
{убыванию.}
{Упорядочение строки матрицы методом пузырька по убыванию.}
for k:=1 to n-1 do
for j :=1 to n-k do
if a [ i, j ] < a [ i, j +1] then
begin
b:=a [ i, j ];
a [ i, j ] : = a [ i, j + 1 ];
a [ i, j +1]:=b;
end;
//Вывод преобразованной матрицы.
writeln ( ’преобразованная матрица A ’ );
for i :=1 to m do
begin
for j :=1 to n do
write ( a [ i, j ] : 7 : 3, ’ ’ );
writeln
end
end.
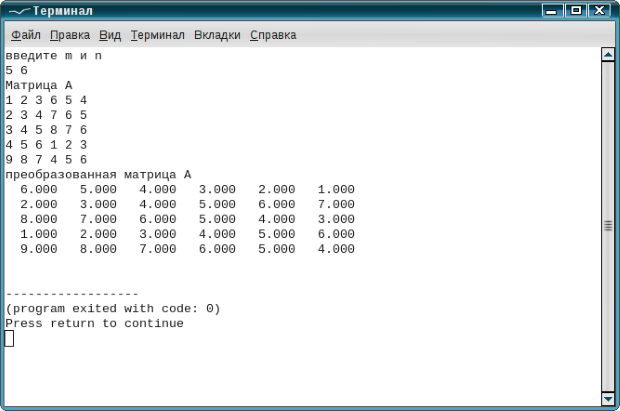
На рис. 6.26 приведены результаты работы программы.
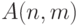 . Сформировать вектор
. Сформировать вектор  , в который записать сумму простых чисел каждой строки матрицы в четверичной системе счисления; если в строке нет простых чисел, в соответствующий элемент массива записать число 0.
, в который записать сумму простых чисел каждой строки матрицы в четверичной системе счисления; если в строке нет простых чисел, в соответствующий элемент массива записать число 0.Для решения этой задачи нам понадобятся функции проверки, является ли число простым, и перевода целого числа в четверичную систему счисления. Алгоритм проверки, является ли число простым, уже неоднократно рассматривался в книге. Функция этой проверки подробно рассматривалась в главе 5 при решении задачи 5.7. Поэтому здесь просто приведем её текст.
function prostoe (N: integer ) : boolean; var i : integer; pr : boolean; begin if N<1 then pr := false else begin pr := true; for i :=2 to N div 2 do if (N mod i = 0) then begin pr := false; break; end; end; prostoe:= pr; end;
В этой же главе 5 мы рассматривали алгоритм (рис. 5.42) и функцию перевода (function perevod(N:real;P:word;kvo:word):real;) вещественного числа в  -чную систему счисления (задача 5.10). Нужная нам функция перевода целого числа в четверичную систему счисления является частным случаем рассмотренной ранее функции perevod. Ниже приведён текст функции perevod4, которая переводит целое положительное число в четверичную систему счисления.
-чную систему счисления (задача 5.10). Нужная нам функция перевода целого числа в четверичную систему счисления является частным случаем рассмотренной ранее функции perevod. Ниже приведён текст функции perevod4, которая переводит целое положительное число в четверичную систему счисления.
{Функция перевода целого числа N в четверичную систему счисления.}
function perevod4 (N: word ) : word;
var s1, i, q, ost : word;
begin
{В переменной s1 мы будем собирать число в четверичной системе}
{счисления.}
s1 : = 0;
{В переменной q будем последовательно хранить степени десяти; вначале}
{туда записываем 1 - десять в 0 степени, а затем в цикле будем}
{последовательно умножать q на 10.}
q : = 1;
{Перевод целого числа, пока число не станет равным 0.}
while (N<>0) do
begin
{Вычисляем ost - очередной разряд числа, как остаток от деления N на 4}
{(основание системы счисления).}
ost :=N mod 4;
{Очередной разряд числа умножаем на 10 в степени i и добавляем к}
{формируемому числу s1.}
s1 := s1+ost * q;
{Уменьшаем число N в 4 раза путем целочисленного деления на 4.}
N1:=N1 div 4;
{Формируем следующую степень десятки.}
q:=q * 10;
end;
//Возвращаем число в четверичной системе счисления.
perevod := s1;
end;
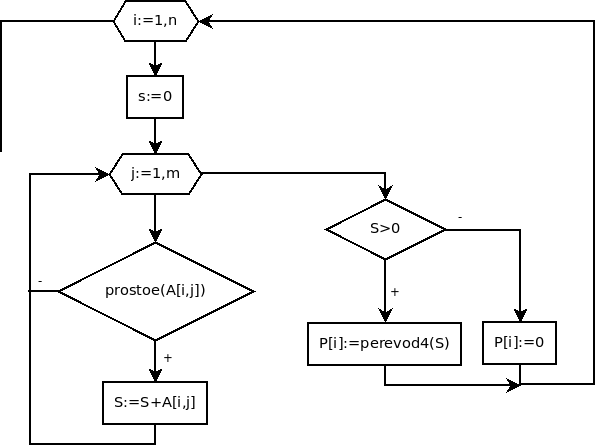
В каждой строке надо найти сумму простых чисел, а затем полученное число перевести в четверичную систему счисления. Поэтому необходимо для каждой строки (i:=1,2,..,n) выполнить следующее: обнулить сумму S (S:=0), организовать цикл по элементам строки (j:=1,2,...,m), внутри которого проверять, является ли текущий элемент Ai,j простым, и если является, добавлять его к сумме S. После выхода из цикла по j необходимо проверить, были ли в строке с номером i простые числа (S>0), и если были, перевести S в четверичную систему счисления и сформировать соответствующий элемент массива P (P[i]:=perevod4(S)).
Блок-схема алгоритма приведена на рис. 6.27.
Полный текст консольного приложения приведён ниже.
program pr_6_9;
function prostoe (N: integer ) : boolean;
var i : integer;
pr : boolean;
begin
if N<1 then pr := false
else
begin
pr := true;
for i :=2 to N div 2 do
if (N mod i = 0) then
begin
pr := false;
break;
end;
end;
prostoe := pr;
end;
function perevod4 (N: word ) : word;
var s1, q, ost : word;
begin
{В переменной s1 мы будем собирать число в четверичной системе}
{счисления.}
s1 : = 0;
{В переменной q будем последовательно хранить степени десяти, вначале}
{туда записываем 1 - десять в 0 степени, а затем в цикле будем}
{последовательно умножать q на 10.}
q : = 1;
{Перевод целого числа, пока число не станет равным 0.}
while (N<>0) do
begin
{Вычисляем ost - очередной разряд числа, как остаток от деления N на 4}
{(основание системы счисления).}
ost :=N mod 4;
{Очередной разряд числа умножаем на 10 в степени i и добавляем к}
{формируемому числу s1.}
s1 := s1+ost * q;
{Уменьшаем число N в 4 раза путем целочисленного деления на 4.}
N:=N div 4;
{Формируем следующую степень десятки.}
q:=q * 1 0;
end;
//Возвращаем число в четверичной системе счисления.
perevod4 := s1;
end;
var S, i, j, n,m: word;
a : array [ 1.. 2 5, 1.. 2 5 ] of word;
p : array [ 1.. 2 5 ] of word;
begin
//Ввод размеров матрицы.
writeln ( ’Введите размеры матрицы ’ );
readln ( n,m);
//Ввод матрицы.
writeln ( ’Введите матрицу A ’ );
for i :=1 to n do
for j :=1 to m do
read (A[ i, j ] );
{Последовательно перебираем все строки матрицы для формирования суммы}
{простых чисел каждой строки.}
for i :=1 to n do
begin
//Вначале сумма равна нулю.
S : = 0;
//Перебираем все элементы в i-й строке матрицы.
for j :=1 to m do
//Если очередной элемент в i-й строке матрицы - простое число,
//то добавляем его к сумме.
if prostoe (A[ i, j ] ) then s := s+A[ i, j ];
{Если в строке были простые числа, то их сумму переводим в четверичную}
{систему счисления и записываем в p[i].}
if s >0 then p [ i ] : = perevod4 ( s )
{Если в строке не было простых чисел, то p[i]:=0.}
else p [ i ] : = 0;
end;
//Вывод сформированного массива P.
writeln ( ’Массив P ’ );
for i :=1 to n do
write (P [ i ], ’ ’ );
writeln;
end.
Результаты работы программы представлены на рис. 6.28.