Численные методы и программирование с Maxima
4.3.4 Оптимизация с использованием пакета lbfgs
Основная функция пакета (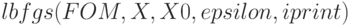 ) позволяет найти приближенное решение задачи минимизации без ограничений целевой функции, определяемой выражением
) позволяет найти приближенное решение задачи минимизации без ограничений целевой функции, определяемой выражением  , по списку переменных
, по списку переменных  с начальным приближением
с начальным приближением  . Критерий окончания поиска определяется градиентом нормы целевой функции (градиент нормы
. Критерий окончания поиска определяется градиентом нормы целевой функции (градиент нормы  ).
).
Данная функция использует квазиньютоновский алгоритм с ограниченной памятью (алгоритм BFGS). Этот метод называют методом с ограниченным использованием памяти, потому что вместо полного обращения матрицы Гессе (гессиана) используется приближение с низким рангом. Каждая итерация алгоритма — линейный (одномерный) поиск, то есть, поиск вдоль луча в пространстве переменных  с направлением поиска, вычисленным на базе приближенного обращения матрицы Гессе. В результате успешного линейного поиска значение целевой функции (
с направлением поиска, вычисленным на базе приближенного обращения матрицы Гессе. В результате успешного линейного поиска значение целевой функции ( ) уменьшается. Обычно (но не всегда) норма градиента
) уменьшается. Обычно (но не всегда) норма градиента  также уменьшается.
также уменьшается.
Параметр функции 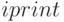 позволяет контролировать вывод сообщений о прогрессе поиска. Величина
позволяет контролировать вывод сообщений о прогрессе поиска. Величина ![iprint[1]](/sites/default/files/tex_cache/fb5623fb41819377d37c7b5907dced7e.png) управляет частотой вывода (
управляет частотой вывода (![iprint[1] < 0](/sites/default/files/tex_cache/94d7a52612541f990c20cef0c179a328.png) — сообщения не выводятся;
— сообщения не выводятся; ![iprint[1] = 0](/sites/default/files/tex_cache/37dc1dbf531e0841d04879638459498a.png) — сообщения на первых и последних итерациях;
— сообщения на первых и последних итерациях; ![iprint[1] > 0](/sites/default/files/tex_cache/c6158a4d92c645e5725a4725afac6cc5.png) — вывод сообщений на каждой
— вывод сообщений на каждой ![iprint[1]](/sites/default/files/tex_cache/fb5623fb41819377d37c7b5907dced7e.png) итерации). Величина
итерации). Величина ![iprint[2]](/sites/default/files/tex_cache/ce710bf0c10a4ea05924c74ca1613524.png) управляет объёмом выводимой информации (если
управляет объёмом выводимой информации (если ![iprint[2] = 0](/sites/default/files/tex_cache/93083b3f4940fa3f0073902e62b44f47.png) , выводится счётчик итераций, число вычислений целевой функции, её величину, величину нормы градиента
, выводится счётчик итераций, число вычислений целевой функции, её величину, величину нормы градиента  и длины шага). Увеличение
и длины шага). Увеличение ![iprint[2]](/sites/default/files/tex_cache/ce710bf0c10a4ea05924c74ca1613524.png) (целая переменная, принимающая значения 0,1,2,3) влечёт за собой увеличение количества выводимой информации.
(целая переменная, принимающая значения 0,1,2,3) влечёт за собой увеличение количества выводимой информации.
Обозначения колонок выводимой информации:
- I — число итераций, которое увеличивается после каждого линейного поиска;
- NFN — количество вычислений целевой функции;
- FUNC — значение целевой функции в конце линейного поиска;
- GNORM — норма градиента целевой функции в конце очередного линейного поиска;
- STEPLENGTH — длина шага (внутренний параметр алгоритма поиска).
Функция 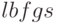 реализована разработчиками на Lisp путём перекодирования классического алгоритма, первоначально написанного на Фортране, поэтому сохранила некоторые архаичные черты. Однако используемый алгоритм обладает высокой надёжностью и хорошим быстродействием.
реализована разработчиками на Lisp путём перекодирования классического алгоритма, первоначально написанного на Фортране, поэтому сохранила некоторые архаичные черты. Однако используемый алгоритм обладает высокой надёжностью и хорошим быстродействием.
Рассмотрим примеры использования  .
.
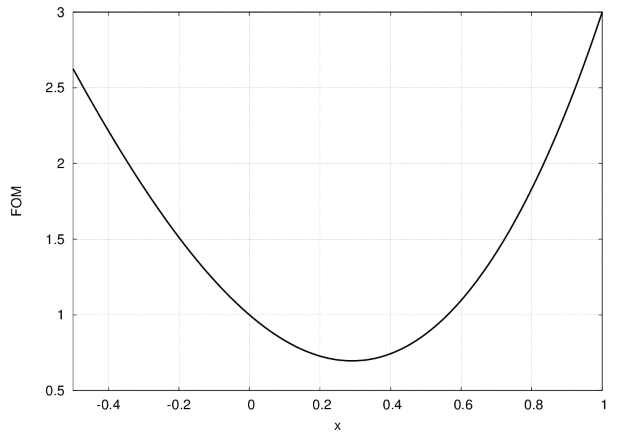
Простейший пример — минимизация функции одной переменной. Необходимо найти локальный минимум функции 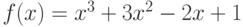 . Результаты расчётов:
. Результаты расчётов:
(%i1) load (lbfgs);
(%i2) FOM:x^3+3*x^2-2*x+1;

(%i3) lbfgs(FOM,[x],[1.1], 1e-4, [1, 0]);
*************************************************
N= 1 NUMBER OF CORRECTIONS=25
INITIAL VALUES
F= 3.761000000000001D+00 GNORM= 8.230000000000001D+00
*************************************************
I NFN FUNC GNORM STEPLENGTH
1 2 8.309999999999997D-01 1.370000000000000D+00 1.215066828675577D-01
2 3 7.056026396574796D-01 3.670279947916664D-01 1.000000000000000D+00
3 4 6.967452517789576D-01 3.053950958095847D-02 1.000000000000000D+00
4 5 6.966851926112383D-01 5.802032710369720D-04 1.000000000000000D+00
5 6 6.966851708806983D-01 8.833119583551152D-07 1.000000000000000D+00
THE MINIMIZATION TERMINATED WITHOUT DETECTING ERRORS.
IFLAG = 0![[x=0.29099433470072]\leqno{(\%o3) }](/sites/default/files/tex_cache/b927c5f1d6c0fc6958d1dba85f186617.png)
Рассмотрим результаты минимизации функции нескольких переменных при помощи  :
:
(%i1) load (lbfgs)$ (%i2) FOM:2*x*y+8*y*z+12*x*z+1e6/(x*y*z);
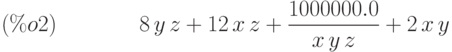
(%i3) lbfgs(FOM,[x,y,z],[1,1,1],1e-4,[-1,0]);
![\%o3)\ [x=13.47613086835734, y=20.21398622934409,\\ z=3.369022781547174]](/sites/default/files/tex_cache/143efc4f6d6e6d3f9735dc1835f64b1f.png)
4.3.4.1 Оптимизация с ограничениями методом неопределённых множителей Лагранжа
Для решения задач минимизации с ограничениями в составе Maxima предусмотрен пакет augmented_lagrangian_method, реализующий метод неопределённых множителей Лагранжа.
Синтаксис вызова функции:

-
 .
.
Рассматриваемая функция возвращает приближенное решение задачи минимизации функции нескольких переменных с ограничениями, представленными в виде равенств. Целевая функция задаётся выражением  , варьируемые переменные — списком
, варьируемые переменные — списком  , их начальные значения — списком
, их начальные значения — списком 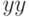 , ограничения — списком
, ограничения — списком  (предполагается, что ограничения приравниваются к 0). Переменные
(предполагается, что ограничения приравниваются к 0). Переменные  задаются в форме символ=значение.
задаются в форме символ=значение.
Распознаются следующие символы:
-
 — число итераций метода неопределённых множителей Лагранжа;
— число итераций метода неопределённых множителей Лагранжа; -
 — точность поиска LBFGS;
— точность поиска LBFGS; -
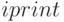 — тот же параметр, что и для
— тот же параметр, что и для 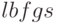 ;
; -
 — начальное значение неопределённого множителя для метода Лагранжа.
— начальное значение неопределённого множителя для метода Лагранжа.
Для использования функции  необходимо загрузить её командой
необходимо загрузить её командой  .
.
Данная реализация метода неопределённых множителей Лагранжа базируется на использовании квазиньютоновского метода LBFGS.