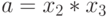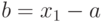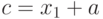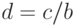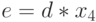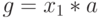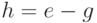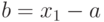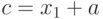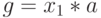Структурно-функциональная организация ЭВМ

Параллельные вычисления

Вычислительный процесс - это последовательность целенаправленных действий по обработке информации, приводящих к достижению поставленной цели.

Вычислительный процесс характеризуется тремя параметрами:

• составом событий, из которых он состоит;
• продолжительностью каждого события (или операций по обработке события);
• последовательностью возникновения событий.

Графически вычислительный процесс может изображаться трассой, временной диаграммой, ярусно-параллельным графом, и др.

Трасса представляется в виде упорядоченного множества событий 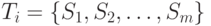, имевших место в моменты времени 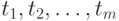, причем

Трасса характеризует динамику процесса, т.е. развитие его во времени. Обычно она изображается в виде последовательности событий, нанесенных в масштабе на ось времени.

Развитие процесса в пространстве и во времени характеризуется временной диаграммой. Временная диаграмма обычно изображается на нескольких осях времени, причем каждая ось содержит трассу, которая характеризует загрузку одного из устройств, выделенных процессу.

Ярусно-параллельный граф характеризует параллельность (одновременность, параллелизм) выполнения действий, составляющих процесс.

Простейший вид параллелизма реализован в мультипрограммных системах - этот вид параллелизма называется "совмещение во времени различных этапов разных задач".

Мультипрограммная обработка возможна и в однопроцессорной системе, так как реализует совмещение во времени выполнение различных частей разных задач. Для такого совмещения лишь необходимо, чтобы однопроцессорная система состояла из относительно независимых, автономных частей, каждая из которых может выполнять свою работу одновременно с работой других. При этом каждая задача все-таки будет решаться последовательно, но разные части вычислительной системы будут одновременно работать над разными задачами, не мешая друг другу.

В вычислительных системах, содержащих несколько обрабатывающих устройств, возможен другой тип параллелизма: одновременное решение различных задач или одновременное решение независимых ветвей одной задачи.

Если в систему поступает непрерывный поток не связанных между собой задач (т. е. таких задач, для которых характерно, что решение любой задачи не зависит от результатов решения других задач), использование нескольких обрабатывающих устройств позволяет совместить решение этих задач во времени. Это - "естественный параллелизм независимых задач".

При решении большой задачи в ней так же могут быть выделены отдельные независимые части - ветви, которые при наличии нескольких обрабатывающих устройств могут выполняться параллельно и независимо друг от друга. Это - "параллелизм независимых ветвей".

Для естественного параллелизма независимых задач и параллелизма независимых ветвей наиболее наглядной формой графического представления является ярусно-параллельная.

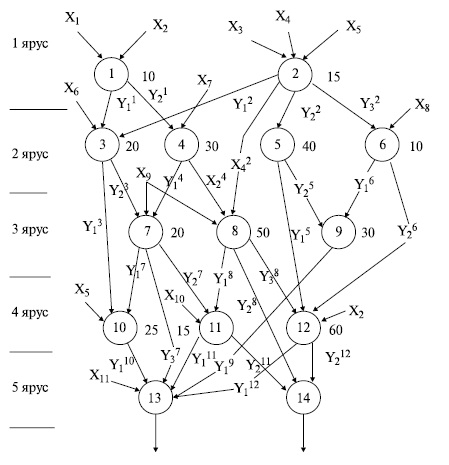
Ярусно-параллельный граф представляет вычислительный процесс в виде совокупности ветвей, расположенных в нескольких уровнях (ярусах). Ветви обозначаются кружками с цифрами внутри. Длина ветви характеризуется цифрой, стоящей около кружка. Стрелками показаны входные данные и результаты обработки. Входные данные обозначаются символами "x", выходные - символами "y". Индексы при "y" есть нижние и верхние. Верхние индексы соответствуют номеру ветви, при выполнении которой получен данный результат. Нижний индекс обозначает порядковый номер результата, полученного при реализации данной ветви программы.

Ветви каждого яруса не связаны друг с другом, т.е. результаты решения какой-нибудь ветви данного яруса не являются входными данными для другой ветви этого же яруса.

На примере ярусно-параллельных графов можно выявить преимущества вычислительных систем, имеющих несколько обрабатывающих устройств, и проблемы, возникающие в таких системах.

Рассмотрим возможности ярусно-параллельного графа на примере параллелизма независимых ветвей одной задачи. Пусть необходимо в параллельной системе произвести вычисление по формуле:

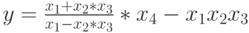
и определить продолжительность вычислений по сравнению с однопроцессорной системой. Будем считать, что сложение и вычитание выполняются за 100 единиц времени, умножение - за 600, деление - за 1000.

В однопроцессорной системе последовательность действий может быть такая:

№	Действие	Время
1		600
2		100
3		100
4		1000
5		600
6		600
7		100
	Итого:	3100

Время на выполнение такой последовательности действий составляет 3100 единиц.

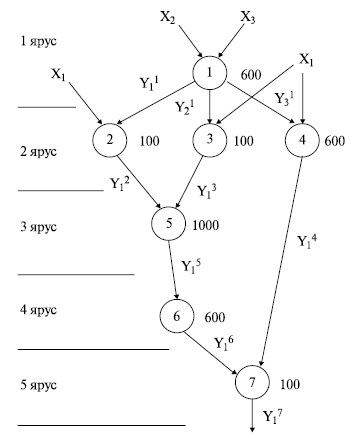
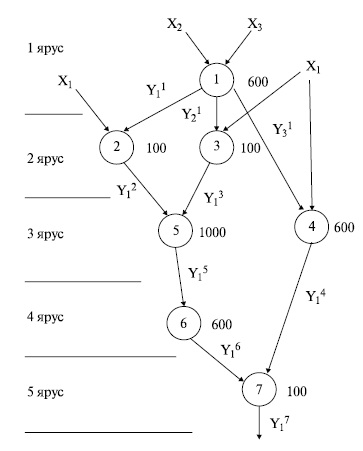
При наличии нескольких процессоров последовательность действий может измениться (рис.16.8):

Рис. 16.8. Пример 1 ярусно-параллельного графа

1. сначала вычисляется

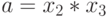
2. затем на разных процессорах одновременно вычисляется:

   • 
   • 
   • 
3. на одном из процессоров вычисляется
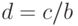
4. затем опять на любом процессоре вычисляется
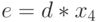
5. и наконец, вычисляется последняя разность .

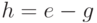Здесь цифры обозначают ярусы.

Продолжительность операции на 1 ярусе - 600 единиц, на втором - тоже 600 (сложение и вычитание закончатся раньше, но критическим для яруса является умножение), на третьем ярусе - 1000 единиц, на четвертом - 600, и на пятом - 100. Итого t1 = 2900 единиц.

Можно самую длинную операцию 2 яруса перенести на 3 ярус. Тогда граф изменится (рис.16.9), ветвь 4 со 2-го яруса переместится на 3.

Рис. 16.9. Пример 2 ярусно-параллельного графа

В этом случае продолжительность 2 яруса станет 100, т.е. уменьшится на 500 единиц, и общее время вычислений станет равным 2400 единиц.

В случае естественного параллелизма независимых задач и большом числе задач ярусно-параллельный граф становится значительно сложнее и допускает значительно большее количество вариантов, как например, на рис.16.10.

Для такого графа характерно, что выигрыш во времени может существенно колебаться в зависимости от последовательности выполнения ветвей каждым обрабатывающим блоком (процессором), поэтому каждый процессор должен выбирать новую ветвь с учетом этого обстоятельства. Перед началом выполнения очередной ветви каждый процессор должен иметь информацию о готовности данных для этого.

Рис. 16.10. Пример 3 ярусно-параллельного графа

Таким образом, чтобы с помощью нескольких обрабатывающих устройств решить задачи, имеющие независимые параллельные ветви, необходима соответствующая организация вычислительного процесса, которая будет определять пути решения задач и вырабатывать необходимую информацию о готовности каждой ветви.

При этом возникают следующие трудности:

1. длительность каждой ветви известна недостаточно точно;
2. трудно избежать некоторых простоев из-за неготовности данных для выполнения той или иной ветви;
3. есть сложности и в оптимизации выделения независимых ветвей. Наличие этих трудностей несколько снижает выигрыш в производительности системы.

Однако при решении многих сложных задач одно только программирование с выделением независимых ветвей уже позволяет существенно сократить время решения.

Хорошо поддаются параллельной обработке такого типа задачи матричной алгебры (в том числе - и компьютерной графики), линейного программирования, спектральной обработки сигналов, преобразования Фурье, задачи кластерного анализа, математической статистики, автоматической классификации, и т.д.

Контрольные вопросы

1. Какие устройства ЭВМ относятся к центральным?
2. В какой последовательности работают блоки микропроцессора при выполнении машинной команды?
3. Объясните разницу между однопрограммным и многопрограммным режимами работы ЭВМ.
4. Чем различаются интерпретаторы и компиляторы?
5. Что такое фрагментация памяти и есть ли какие-либо способы ее избежать?
6. Для чего используется динамическая трансляция адресов?
7. Какую структуру имеет адрес операнда при сегментно-страничной организации памяти?
8. Для чего предназначен вектор прерывания и какую структуру он имеет?