Обработка данных
Процессам обработки, в том числе и обработке данных, присуще свойство, заключающееся в том, что обработка состоит из нескольких стадий, этапов, операций, которые могут рассматриваться как более простые процессы (подпроцессы) обработки. Стадии обработки могут быть взаимосвязаны. Выполнение тех или иных этапов обработки зависит от результатов выполнения других этапов.
Описание процессов обработки осуществляется в виде совокупности предписаний или достаточно простых действий, которые должны быть выполнены для придания объекту обработки желаемых свойств. Подобные описания, представленные в формализованном виде, обычно называются алгоритмами.
Для исследования процессов обработки данных используются различные формальные модели: конечные автоматы, сети Петри, взаимодействующие последовательные процессы Хоара, системы и сети массового обслуживания и многие другие. Они описывают различные аспекты процессов обработки. Некоторые из этих моделей рассматриваются далее.
Описание процесса обработки данных. Понятие алгоритма и его свойства. Способы формальной записи алгоритмов
В повседневной жизни часто встречаются различного рода предписания, инструкции и другие подобные документы, определяющие порядок действий, которые необходимо выполнить для достижения определенного результата. Примерами таких документов являются инструкции по использованию различных устройств (бытовых приборов, банкоматов, торговых автоматов и т.п.), правила выполнения работ в промышленности и строительстве, регламенты совершения различных действий (банковских операций, сделок на фондовых валютных и товарных биржах, проверок технического состояния оборудования и объектов и т.п.). Эти предписания могут отличаться различной степенью точности и детальности описания действий. Если предполагается, что исполнителем предпи-саний будет некоторое устройство (агрегат, станок, транспортное средство или ЭВМ), то предписание будет написано на некотором формальном языке. Типичным примером такого предписания является компьютерная программа, написанная на некотором языке программирования. Обобщением различного рода инструкций и предписаний является понятие алгоритма [27], [35].
Алгоритм - это точное, т. е. сформулированное на определенном языке, конечное описание того или иного общего метода, основанного на применении исполнимых элементарных тактов обработки.
Рассмотрим более подробно отдельные аспекты данного определения. Во-первых, в определении говорится, что описание должно быть точным. Точность описания необходима для того, чтобы обеспечить однозначность понимания действий, которые требуется выполнять, и последовательности их выполнения. В зависимости от того, для кого предназначен алгоритм, точность его описания может быть различной. Если алгоритм предназначен для выполнения человеком, то он может быть описан на естественном языке, например, на русском. В этом случае однозначному пониманию алгоритма не мешают некоторые орфографические ошибки или безобидные опечатки. Если алгоритм должен выполняться автоматическим устройством, то описание алгоритма выполняется на некотором формальном языке (см. п. 6.3), например, на языке инструкций вычислительной системы или языке программирования высокого уровня. Важно также, чтобы описание было конечным, чтобы его можно было загрузить (прочитать) за конечное время.
Во-вторых, важную роль в алгоритме играют элементарные шаги или действия, с помощью которых выполняется алгоритм. Эти действия должны быть достаточно конкретно описаны, чтобы однозначно интер-претироваться исполнителем. Алгоритм для исполнителя должен включать только те команды (элементарные действия), которые ему (исполнителю) доступны. Например, если алгоритм предназначен для выполнения на ЭВМ, то элементарные действия должны входить в систему команд ЭВМ.
В-третьих, алгоритмы, как правило, предназначены для решения не только частных задач (выполнения преобразований конкретных исходных данных), но и для решения целых классов задач. Подлежащие решению частные задачи выделяются из рассматриваемого класса выбором параметров алгоритма. Параметры играют роль исходных данных для алгоритма (процедуры преобразования исходных данных в результат). Например, может быть задан алгоритм, который осуществляет сложение любых двух натуральных чисел. Такому алгоритму нужны два натуральных числа в их десятичном представлении в качестве исходных данных, и он вырабатывает одно число в десятичном представлении как выходные данные (результат).
Алгоритмы характеризуются различными свойствами в зависимости от особенностей процесса их исполнения [26], [35]. Алгоритм называется терминистическим или завершающимся, если он всегда (для всех допустимых исходных данных) заканчивается после конечного числа шагов.
Алгоритм называется детерминистическим, если в процессе его выполнения нет никакой свободы в выборе очередного шага обработки.
Алгоритм называется детерминированным или однозначным, если результат алгоритма определен однозначно (даже если некоторые шаги алгоритма не определены однозначно).
Рассмотрим примеры алгоритмов.
Алгоритм вычисления значения дроби 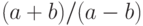 . Сначала вычисляются (используя алгоритмы сложения и вычитания) значения выражений
. Сначала вычисляются (используя алгоритмы сложения и вычитания) значения выражений  и
и  (в любой последовательности), потом находится частное от деления полученных результатов (используя алгоритм деления).
(в любой последовательности), потом находится частное от деления полученных результатов (используя алгоритм деления).
Этот пример демонстрирует иерархическую структуру алгоритмов. Алгоритм вычисления дроби 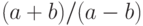 основан на алгоритмах сложения, вычитания и деления чисел. Из того, что операции
основан на алгоритмах сложения, вычитания и деления чисел. Из того, что операции  и
и  могут выполняться в любой последовательности, следует, что этот алго-ритм не детерминистический, но детерминированный. Очевидно, что алгоритм завершающийся (достаточно всего трех элементарных действий: сложения, вычитания и деления).
могут выполняться в любой последовательности, следует, что этот алго-ритм не детерминистический, но детерминированный. Очевидно, что алгоритм завершающийся (достаточно всего трех элементарных действий: сложения, вычитания и деления).
Алгоритм вставки карточки в упорядоченную картотеку. Постановка задачи. Имеется колода карт. Пусть на каждой карте зафиксировано одно натуральное число. Требуется вставить карточку в картотеку, не нарушив упорядоченности картотеки.
В случае пустой картотеки (в картотеке нет карточек) вставка карточки тривиальна. В противном случае раскроем картотеку в произвольном месте и сравним записанное на открывшейся карточке число с числом на вставляемой карточке. В соответствии с результатом этого сравнения будем действовать тем же самым способом, вставляя карточку соответственно в переднюю или хвостовую часть картотеки. Процесс заканчивается, когда карточку нужно вставлять в пустое множество карт.
Очевидно, что этот алгоритм - завершающийся. Если все числа на карточках различны, то этот алгоритм - детерминированный. Однако из-за произвольности места, в котором раскрывается картотека, алгоритм не является детерминистическим.
Алгоритм для вычисления наибольшего общего делителя (НОД) двух натуральных чисел. Постановка задачи. Пусть даны два натуральных числа  , где
, где 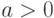 и
и 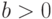 ; надо найти наибольший общий делитель НОД
; надо найти наибольший общий делитель НОД 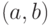 чисел
чисел  и
и  .
.
Еще в III веке до нашей эры математик Евклид, известный автор первого дошедшего до нас теоретического трактата по математике "Начала", в геометрической форме изложил правило получения наибольшего общего делителя двух натуральных чисел. Идея этого правила (обоснование его корректности) заключается в том, что если НОД 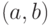 - наибольший общий делитель двух натуральных чисел
- наибольший общий делитель двух натуральных чисел  и
и  , то в случае равенства этих чисел он совпадает с любым из них, а в случае их неравенства разность между большим и меньшим вместе с меньшим имеет тот же самый наибольший общий делитель. Назовем число, равное тому из двух чисел
, то в случае равенства этих чисел он совпадает с любым из них, а в случае их неравенства разность между большим и меньшим вместе с меньшим имеет тот же самый наибольший общий делитель. Назовем число, равное тому из двух чисел  , которое не меньше другого, их верхней гранью и обозначим
, которое не меньше другого, их верхней гранью и обозначим  , а второе обозначим
, а второе обозначим  . После вычитания одного числа из другого получим новую пару чисел
. После вычитания одного числа из другого получим новую пару чисел 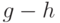 и
и  , верхняя грань
, верхняя грань 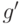 которых строго меньше
которых строго меньше  . Новые числа имеют тот же наибольший общий делитель НОД
. Новые числа имеют тот же наибольший общий делитель НОД 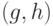 . Значит, мы свели задачу к нахождению наибольшего общего делителя натуральных чисел, верхняя грань которых меньше первоначальной.
. Значит, мы свели задачу к нахождению наибольшего общего делителя натуральных чисел, верхняя грань которых меньше первоначальной.
Повторяя прием, мы должны, в конце концов, прийти к случаю, когда новые полученные натуральные числа между собой равны, так как безграничное число шагов уменьшения верхней грани невозможно (потому что натуральных чисел, не превосходящих числа  , всего несколько).
, всего несколько).
Сам алгоритм нахождения наибольшего общего делителя НОД 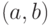 двух натуральных чисел
двух натуральных чисел  и
и  (алгоритм Евклида) можно изложить так:
(алгоритм Евклида) можно изложить так:
- если
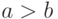 , то перейти к п. 4, иначе перейти к п. 2;
, то перейти к п. 4, иначе перейти к п. 2; - если
 , то перейти к п. 5, иначе перейти к п. 3;
, то перейти к п. 5, иначе перейти к п. 3; - считать, что НОД
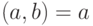 . Конец;
. Конец; - от
 отнять
отнять  и впредь считать, что эта разность является значением
и впредь считать, что эта разность является значением  . Возвратиться к п. 1;
. Возвратиться к п. 1; - от
 отнять
отнять  и впредь считать эту разность значением
и впредь считать эту разность значением  . Возвра-титься к п. 1.
. Возвра-титься к п. 1.
Для алгоритма Евклида арифметическая операция "-" и проверка выполнения отношений "<" и "=" считаются эффективными элементарными шагами обработки. Очевидно, что данный алгоритм является завер-шающимся. Однако если в постановке задачи опустить ограничения 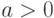 и
и 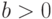 , то получается алгоритм, который для неравных отрицательных чисел не прерывается, то есть не является завершающимся. Кроме того, данный алгоритм является детерминистическим, то есть для каждых исходных данных последовательность отдельных шагов точно определена.
, то получается алгоритм, который для неравных отрицательных чисел не прерывается, то есть не является завершающимся. Кроме того, данный алгоритм является детерминистическим, то есть для каждых исходных данных последовательность отдельных шагов точно определена.
Для рассмотренных достаточно простых алгоритмов их свойства (детерминистичность, детерминированность, завершаемость) легко устанавливаются. Однако в общем случае различные свойства алгорит-мов необходимо доказывать. Доказательство свойств алгоритмов относится к проблематике теории алгоритмов. Одним из важнейших вопросов, которым занимается теория алгоритмов, является выяснение того факта, что алгоритм решает сформулированную задачу для заданного множества исходных данных. Представляет интерес также нахождение множества исходных данных, на котором алгоритм решает сформулированную задачу.
В приведенных выше примерах описаний алгоритмов все время встречались некоторые похожие друг на друга фрагменты. Так, некоторые шаги алгоритма могут выполняться лишь при определенном условии, или выполнение некоторых шагов производится неоднократно. Часто также поставленная задача решается с помощью решения той же самой задачи, но с другими исходными данными (более простыми). В этих случаях говорят о разветвлении, повторении и рекурсии.
Классические элементы, которые встречаются в описаниях алгоритмов, - это:
- выполнение элементарных шагов;
- разветвления по условиям;
- повторения;
- рекурсии.
В примере с вычислением дроби мы имеем наиболее простой случай: количество элементарных тактов обработки постоянно и не зависит от чисел a, b. Иначе обстоит дело в других примерах: в случае алгоритма Евклида число шагов обработки зависит от величин чисел a, b, в случае алгоритма карточки число шагов зависит от размера картотеки. Хотя описание алгоритма конечно и постоянно, количество фактически выполняемых тактов - величина переменная; это часто является следствием использованию приема, сводящего общую задачу к более простой задаче того же класса. Этот прием называют рекурсией. В алгоритме Евклида и алгоритме вставки карточки в упорядоченную картотеку наличие рекурсии очевидно из алгоритма. В алгоритмах часто используется специальный случай рекурсии - чисто повторительная рекурсия. При описании алгоритма ее часто записывают в форме итерации: "Пока выполнено определенное условие, повторять...".
Наряду с рекурсией и повторением в алгоритмах встречается также анализ возможных случаев. Без анализа отдельных случаев и выявления условий завершения было бы невозможно окончание рекурсивных алгоритмов.
Способы описания алгоритмов. Алгоритмы обрабатывают определенные объекты в качестве исходных данных ("входные") и выдают другие объекты в качестве результатов. Объекты могут быть конкретными, как, например, десятичное число в случае алгоритма сложения десятичных чисел, или абстрактными, как, скажем, натуральные числа (для которых могут использоваться разнообразные эквивалентные системы предста-вления) в случае нахождения наибольшего общего делителя. Для описанного ранее алгоритма нахождения НОК совершенно не существенно, записываются числа в десятичной или двоичной системе счисления или даже римскими цифрами: свойства делимости от этого не меняются. В теоретических исследованиях предпочитают опираться на алгоритмы, которые работают, например, только с натуральными числами (Гедель) либо только с цепочками знаков (Марков). С практической точки зрения нет никакой пользы или нужды в таких ограничениях, допустимы какие угодно множества объектов, если только можно аккуратно определить их свойства. Разве лишь, поскольку приходится привлекать разбор отдельных случаев, необходимо включить в множество объектов, по крайней мере, значения истинности "истина" и "ложь". В зависимости от того, какие допускаются классы объектов (и соответствующих операций), приходят к различным классам алгоритмов.
Рассмотрим чуть более подробно специальную запись алгоритмов преобразования последовательностей знаков [27], [35]. Такая запись пред-ставляет собой один из способов уточнения понимавшегося до сих пор интуитивно понятия алгоритма.
Без сомнения, элементарной операцией над последовательностями знаков может считаться замена подслова на некоторое слово (текстовая замена). Будем исходить из множеств  и
и  слов над общим набором знаков (алфавитом)
слов над общим набором знаков (алфавитом)  . Отдельную операцию замены, которую также называют продукцией, будем записывать в виде
. Отдельную операцию замены, которую также называют продукцией, будем записывать в виде  и понимать ее следующим образом.
и понимать ее следующим образом.
Если  является подсловом заданного слова
является подсловом заданного слова 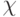 , то заменить это под-слово на
, то заменить это под-слово на  . В случае если подслово
. В случае если подслово  встречается в
встречается в 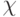 несколько раз, словом
несколько раз, словом  заменяется то из них, которое стоит в самой левой позиции.
заменяется то из них, которое стоит в самой левой позиции.
Далее, если дано конечное множество таких продукций, перечисленных в определенном порядке, то текстовая замена должна производиться посредством применения самой первой (относительно этого порядка) из применимых продукций. Все это повторяется до тех пор, пока возможно, или же до применения особым образом отмеченной продукции ("останавливающей"). Учитывая, что одно из слов в продукции может быть пустым словом (см. 2.1.3), текстовая замена включает в себя вставку и присоединение знаков, а также вычеркивание знаков.
Такого рода алгоритмы называют алгоритмами Маркова по имени советского математика А. А. Маркова, который впервые описал их в 1951 г. Сам Марков называл их "нормальными алгоритмами". Их можно считать уточнением понятия алгоритма, достигаемым за счет использования специальной формы описания. Существуют и другие подходы к уточнению (формализации) понятия алгоритма, используемые, в основном, для теоретических исследований.
Для практических целей часто используют графические способы описания алгоритмов, которые являются более компактными и наглядными. При графическом описании каждая операция процесса обработки изображается отдельной стандартной геометрической фигурой (блоком).
Некоторые стандартные блоки, их назначение и краткое описание приведены в таблице.
Блоки соединяются линиями переходов, определяющими очередность выполнения действий. Такое графическое представление называется схемой алгоритма или блок-схемой. Набор символов, используемых в блок-схемах, и правила изображения блок-схем в настоящее время определяются ГОСТ 19.701 - 90 (ИСО 5807 - 85) "Единая система программной документации. Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения".