Информационно-логические основы ЭВМ
Машинные коды
Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (нуль или единица) перед его старшим числовым разрядом.
Пример 14.5.
![A_{10} = +10\; A_2 = +1010\; [А_2]_п=0 \vdots 1010; \\
B_{10}=-15\; B_2=-1111 \; [B_2]_n=1 \vdots 1111](/sites/default/files/tex_cache/cd6cac24728b82ff5d105a91280a1afe.png)
Точечной вертикальной линией здесь отмечена условная граница, отделяющая знак от цифровых разрядов.
Обратный код двоичного числа образуется по следующему правилу. Обратный код положительных чисел совпадает с их прямым кодом. Обратный код отрицательного числа содержит единицу в знаковом разряде числа, а значащие разряды числа заменяются инверсными, т.е. нули заменяются единицами, а единицы - нулями.
Пример 14.6.
![А_{10} = +5\; А_2=+101\; [А_2]_n=[А_2]_{ОК} = 0 \vdots 101; \\
В_{10}=-13\; В_2=-1101\; [B_2]_{0K}=1 \vdots 0010.](/sites/default/files/tex_cache/7f234a1a8a59963ab20d73d6cc19a0cf.png)
Свое название обратный код чисел получил потому, что коды цифр отрицательного числа заменены инверсными. Укажем наиболее важные свойства обратного кода чисел:
- сложение положительного числа
 с его отрицательным значением в обратном коде дает так называемую машинную единицу
с его отрицательным значением в обратном коде дает так называемую машинную единицу  , состоящую из единиц в знаковом и значащих разрядах числа;
, состоящую из единиц в знаковом и значащих разрядах числа; - нуль в обратном коде имеет двоякое значение. Он может быть положительным числом -
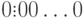 и отрицательным числом -
и отрицательным числом - 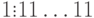 . Значение отрицательного нуля совпадает с
. Значение отрицательного нуля совпадает с  . Двойственное представление нуля явилось причиной того, что в современных ЭВМ все числа представляются не обратным, а дополнительным кодом.
. Двойственное представление нуля явилось причиной того, что в современных ЭВМ все числа представляются не обратным, а дополнительным кодом.
Дополнительный код положительных чисел совпадает с их прямым кодом. Дополнительный код отрицательного числа представляет собой результат суммирования обратного кода числа с единицей младшего разряда (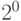 - для целых чисел,
- для целых чисел, 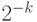 - для дробных).
- для дробных).
Пример 14.7.
![А_{10} =+19\; A_2=+10011\; [A_2]_n=[A_2]_{OK}=[A_2]_{ДК}=0 \vdots 10011;\\
B_{10}=-13\; B_2=-11-1\; [B_2]_{ДК}=[B_2]_{OK}+2^0=1 \vdots 0010+1=1 \vdots 0011](/sites/default/files/tex_cache/390cbb47e5b4fc6018e82104add592e2.png)
Укажем основные свойства дополнительного кода.
-
Сложение дополнительных кодов положительного числа
 с его отрицательным значением дает так называемую машинную единицу дополнительного кода:
с его отрицательным значением дает так называемую машинную единицу дополнительного кода:
т. е. число 10 (два) в знаковых разрядах числа.
- Дополнительный код получил такое свое название потому, что представление отрицательных чисел является дополнением прямого кода чисел до машинной единицы
 .
. - Нуль в дополнительном коде имеет единственное представление. Благодаря этому все современные компьютеры используют при хранении и преобразовании чисел именно двоичный код.
Модифицированные обратные и дополнительные коды двоичных чисел отличаются соответственно от обратных и дополнительных кодов удвоением значений знаковых разрядов. Знак "+" в этих кодах кодируется двумя нулевыми знаковыми разрядами, а "-" - двумя единичными разрядами.
Пример 14.8.
![А_{10} = 9;\; A_2=+1001;\; [A_2]_n=[A_2]_{ок}=[A_2]_{ДK}= 0 \vdots 1001;\\
\[[A_2\]]_{мок}=[A_2]_{мдк}=00 \vdots 1001;\\
В_{10}=- 9;\; В_2 =-1001;\; [В_2]_{ок}= 1 \vdots 0110 \; [B_2]_{ДК}=1\vdots 0111;\\
\[[B_2\]]_{мок}=11 \vdots 0110; [B_2]_{МДК}=11 \vdots 0111.](/sites/default/files/tex_cache/d96fd35c9ff643a54fac5190c297cdd6.png)
Целью введения модифицированных кодов является фиксация и обнаружение случаев получения неправильного результата, когда значение результата превышает максимально возможный результат в отведенной разрядной сетке машины. В этом случае перенос из значащего разряда может исказить значение младшего знакового разряда. Значение знаковых разрядов "01" свидетельствует о положительном переполнении разрядной сетки, а "10" - об отрицательном переполнении. В настоящее время практически во всех моделях ЭВМ, в том числе во всех ПК, роль удвоенных разрядов для фиксации переполнения разрядной сетки играют переносы, идущие в знаковый и из знакового разряда.
Арифметические операции над числами с фиксированной точкой
Сложение (вычитание). Операция вычитания приводится к операции сложения путем преобразования чисел в обратный (ОК) или дополнительный (ДК) код. Пусть числа 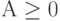 и
и  , тогда операция алгебраического сложения выполняется в соответствии с табл. 14.3.
, тогда операция алгебраического сложения выполняется в соответствии с табл. 14.3.
| Требуемая операция | Необходимое преобразование |
|---|---|
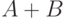 |
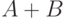 |
 |
 |
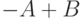 |
 |
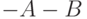 |
 |
Зависимости, представленные в правой части таблицы, указывают на замену операции вычитания операцией сложения с обратным или дополнительным кодом соответствующего числа. Сложение двоичных чисел осуществляется последовательно, поразрядно в соответствии с табл. 14.2. При выполнении сложения цифр необходимо соблюдать следующие правила.
- Слагаемые должны иметь одинаковое число разрядов. Для выравнивания разрядной сетки слагаемых можно дописывать незначащие нули слева к целой части числа и незначащие нули справа к дробной части числа.
- Знаковые разряды чисел участвуют в сложении так же, как и цифровые.
- Необходимые преобразования кодов (п. 14.2) производятся с изменением знаков чисел. Приписанные незначащие нули изменяют свое значение при преобразованиях по общему правилу.
- При образовании единицы переноса из старшего знакового разряда, в случае использования ОК, эта единица складывается с младшим числовым разрядом. При использовании ДК единица переноса теряется. Знак результата формируется автоматически, результат представляется в том коде, в котором представлены исходные слагаемые.
Пример 14.9. Сложить два числа  .
.
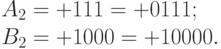
Исходные числа имеют различную разрядность, и необходимо провести выравнивание разрядной сетки:
![[A_2]_п =[A_2]_{ок}= [A_2]_{ДК}=0 \vdots 00111;\\
\[[B_2\]]_п=[B_2]_{ок}=[B_2]_{ДК}=0 \vdots 10000.](/sites/default/files/tex_cache/14664f3c4174c8a0d735b1b571a9cd0a.png)
Сложение в обратном или дополнительном кодах дает один и тот же результат:
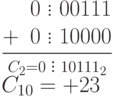
Обратим внимание, что при сложении цифр отсутствуют переносы в знаковый разряд и из знакового разряда, что свидетельствует о получении правильного результата.
Пример 14.10. Сложить два числа 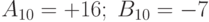 в ОК и ДК.
В соответствии с табл. 14.3 должна быть реализована зависимость
в ОК и ДК.
В соответствии с табл. 14.3 должна быть реализована зависимость  , в которой второй член преобразуется с учетом знака
, в которой второй член преобразуется с учетом знака
![[A_2]_п=0\; \vdots \; 10000=0 \; \vdots \;10000;\;[A_2]_{oк}=0 \vdots \; 10000;\; [A_2]={ДК}=0 \; \vdots \; 10000\\
\[[B_2\]] _п=1\;\vdots111=1\;\vdots\;00111;\; [B_2]_{ок}=1\;\vdots \;11000;\;[B_2]_{ДК}=1\;\vdots\;11001](/sites/default/files/tex_cache/498b5823f493b632a1f70306f7770303.png)
При сложении чисел в ОК и ДК были получены переносы в знаковый разряд и из знакового разряда. В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда (см. п. 4. правил). В случае ДК этот перенос игнорируется.
Умножение. Умножение двоичных чисел наиболее просто реализуется в прямом коде. Рассмотрим, каким образом оно приводится к операциям сложения и сдвигам.
Пример 14.11. Умножить два числа 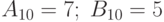 . Перемножим эти числа, представленные прямыми двоичными кодами, так же, как это делается в десятичной системе.
. Перемножим эти числа, представленные прямыми двоичными кодами, так же, как это делается в десятичной системе.
Нетрудно видеть, что произведение получается путем сложения частных произведений, которые представляют собой разряды множимого, сдвинутые влево в соответствии с позициями разрядов множителя. Частные произведения, полученные умножением на нуль, игнорируются. Важной особенностью операции умножения n-разрядных сомножителей является увеличение разрядности произведения до  . Знак произведения формируется путем сложения знаковых разрядов сомножителей. Возможные переносы из знакового разряда игнорируются.
. Знак произведения формируется путем сложения знаковых разрядов сомножителей. Возможные переносы из знакового разряда игнорируются.
Деление. Операция деления, как и в десятичной арифметике, является обратной операции умножения. Покажем, что и эта операция приводится к последовательности операций сложения и сдвига.
Пример 14.12. Разделить два числа  .
.
![[А_2]_п= 101101\\
\[[B_2\]]_п=101](/sites/default/files/tex_cache/4b2a62ef38526468a40b5eed915a109f.png)
Деление произведено так же, как это делается обычно в десятичной системе. Сначала проверяется, можно ли вычесть значение делителя из старших разрядов делимого. Если возможно, то в разряде частного записывается единица и определяется частная разница. В противном случае в частное записывается нуль, и разряды делителя сдвигаются вправо на один разряд по отношению к разрядам делимого. К полученной предыдущей разнице сносится очередная цифра делимого, и данный процесс повторяется, пока не будет получена необходимая точность. Если учесть, что все вычитания в ЭВМ заменяются сложением в ОК или в ДК (см. табл. 14.3), то действительно, операция деления приводится к операциям сложения и сдвигам вправо разрядов делителя относительно разрядов делимого. Отметим, что делимое перед операцией деления должно быть приведено к  -разрядной сетке. Только в этом случае при делении на
-разрядной сетке. Только в этом случае при делении на  -разрядный делитель получается
-разрядный делитель получается  -разрядное частное.
-разрядное частное.
Знак частного формируется также путем сложения знаковых разрядов делимого и делителя, как это делалось при умножении.



