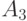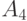Информационные технологии
Неравномерное кодирование. Средняя длина кодирования
В приведенных выше примерах кодирования все кодовые слова имели одинаковую длину. Однако это не является обязательным требованием. Более того, если вероятности появления сообщений заметно отличаются друг от друга, то сообщения с большой вероятностью появления лучше кодировать короткими словами, а более длинными словами кодировать редкие сообщений. В результате кодовый текст при определенных условиях станет в среднем короче.
Показателем экономичности или эффективности неравномерного кода является не длина отдельных кодовых слов, а "средняя" их длина, определяемая равенством:

где  - кодовое слово, которым закодировано сообщение
- кодовое слово, которым закодировано сообщение  , а
, а  - его длина,
- его длина, 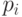 - вероятность сообщения
- вероятность сообщения  ,
, - общее число сообщений источника
- общее число сообщений источника  . Для краткости записи формул далее могут использоваться обозначения
. Для краткости записи формул далее могут использоваться обозначения  и
и 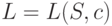 . Заметим, что обозначение средней длины кодирования через
. Заметим, что обозначение средней длины кодирования через 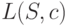 подчеркивает тот факт, что эта величина зависит как от источника сообщений
подчеркивает тот факт, что эта величина зависит как от источника сообщений  , так и от способа кодирования
, так и от способа кодирования  .
.
Наиболее экономным является код с наименьшей средней длиной 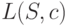 . Сравним на примерах экономичность различных способов кодирования одного и того же источника.
. Сравним на примерах экономичность различных способов кодирования одного и того же источника.
Пусть источник содержит 4 сообщения  с вероятностями
с вероятностями  . Эти сообщения можно закодировать кодовыми словами постоянной длины, состоящими из двух знаков, в алфавите
. Эти сообщения можно закодировать кодовыми словами постоянной длины, состоящими из двух знаков, в алфавите  в соответствии с кодовой таблицей.
в соответствии с кодовой таблицей.
Очевидно, что для представления (передачи) любой последовательности в среднем потребуется 2 знака на одно сообщение. Сравним эффективность такого кодирования с описанным выше кодированием словами переменной длины. Кодовая таблица для данного случая может иметь следующий вид.
В этой таблице, в отличие от предыдущей, наиболее частые сообщения  и
и  кодируются одним двоичным знаком. Для последнего варианта кодирования имеем
кодируются одним двоичным знаком. Для последнего варианта кодирования имеем

в то время как для равномерного кода средняя длина  (она совпадает с общей длиной кодовых слов). Из рассмотренного примера видно, что кодирование сообщений словами различной длины может дать суще-ственное (почти в два раза) увеличение экономичности кодирования.
(она совпадает с общей длиной кодовых слов). Из рассмотренного примера видно, что кодирование сообщений словами различной длины может дать суще-ственное (почти в два раза) увеличение экономичности кодирования.
При использовании неравномерных кодов появляется проблема, которую поясним на примере последней кодовой таблицы. Пусть при помощи этой таблицы кодируется последовательность сообщений  , в результате чего она преобразуется в следующий двоичный текст: 010110. Первый знак исходного сообщения декодируется однозначно - это
, в результате чего она преобразуется в следующий двоичный текст: 010110. Первый знак исходного сообщения декодируется однозначно - это  . Однако дальше начинается неопределенность:
. Однако дальше начинается неопределенность:  или
или  . Это лишь некоторые из возможных вариантов декодирования исходной последовательности знаков.
. Это лишь некоторые из возможных вариантов декодирования исходной последовательности знаков.
Необходимо отметить, что неоднозначность декодирования слова появилась несмотря на то, что условие однозначности декодирования знаков (инъективность кодового отображения) выполняется.
Существо проблемы - в невозможности однозначного выделения кодовых слов. Для ее решения следовало бы отделить одно кодовое слово от другого. Разумеется, это можно сделать, но лишь используя либо паузу между словами, либо специальный разделительный знак, для которого необходимо особое кодовое обозначение. И тот, и другой путь, во-первых, противоречат описанному выше способу кодирования слов путем конкатенации кодов  знаков
знаков  , образующих слово, и, во-вторых, приведет к значительному удлинению кодового текста, сводя на нет преимущества использования кодов переменной длины.
, образующих слово, и, во-вторых, приведет к значительному удлинению кодового текста, сводя на нет преимущества использования кодов переменной длины.
Решение данной проблемы заключается в том, чтобы иметь возможность в любом кодовом тексте выделять отдельные кодовые слова без использования специальных разделительных знаков. Иначе говоря, необходимо, чтобы код удовлетворял следующему требованию: всякая последовательность кодовых знаков может быть единственным образом разбита на кодовые слова. Коды, для которых последнее требование выполнено, называются однозначно декодируемыми (иногда их называют кодами без запятой).
Рассмотрим код (схему алфавитного кодирования)  , заданный кодовой таблицей
, заданный кодовой таблицей
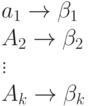
и различные слова, составленные из элементарных кодов.
Определение. Код  называется однозначно декодируемым, если
называется однозначно декодируемым, если

и

то есть любое слово, составленное из элементарных кодов, единственным образом разлагается на элементарные коды.
Если таблица кодов содержит одинаковые кодовые слова, то есть если

то код заведомо не является однозначно декодируемым (схема не является разделимой). Такие коды далее не рассматриваются.
Префиксные коды
Наиболее простыми и часто используемыми кодами без специального разделителя кодовых слов являются так называемые префиксные коды [29].
Определение. Код, обладающий тем свойством, что никакое кодовое слово не является началом (префиксом) другого кодового слова, называется префиксным.
Теорема 1. Префиксный код является однозначно декодируемым.
Доказательство. Предположим противное. Тогда существует слово  которое можно представить двумя разными способами
которое можно представить двумя разными способами  , причем до номера
, причем до номера  все подслова в обоих представлениях (разложениях) совпадают, а слова
все подслова в обоих представлениях (разложениях) совпадают, а слова  и
и  различны. Отбросив одинаковые префиксы двух равных слов (представлений), получим совпадающие окончания
различны. Отбросив одинаковые префиксы двух равных слов (представлений), получим совпадающие окончания 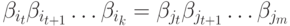 , начинающиеся с различных слов. Из-за равенства окончаний первые буквы слов
, начинающиеся с различных слов. Из-за равенства окончаний первые буквы слов  и
и  должны совпадать. По аналогичной причине должны совпадать и вторые буквы этих слов и т.д. Это означает, что неравенство слов
должны совпадать. По аналогичной причине должны совпадать и вторые буквы этих слов и т.д. Это означает, что неравенство слов  и
и  может заключаться только в том, что они имеют разную длину и, следовательно, одно из них является префиксом другого. Это противоречит префиксности кода.
может заключаться только в том, что они имеют разную длину и, следовательно, одно из них является префиксом другого. Это противоречит префиксности кода.
Множество кодовых слов можно графически изобразить как поддерево словарного дерева (рис.6.5). Для этого из всего словарного дерева следует показать только вершины, соответствующие кодовым словам, и пути, ведущие от этих вершин к корню дерева. Такое поддерево называют деревом кода или кодовым деревом.
На рис.6.5 а) - дерево, соответствующие коду, у которого все слова имеют одинаковую длину. Кружками помечены те вершины, которые соответствуют кодовым словам. В данном случае это 4 двухбуквенных слова, составляющих второй уровень словарного дерева (универсума). Нетрудно понять, как отражается свойство префиксности или его отсутствие на кодовом дереве. Рассмотрим код, состоящий из слов (0, 10, 111). Это не полный префиксный код, так как к коду можно добавить слово 110, которое получается из слова 11 приписыванием справа 0. Эта операция показана на рис.6.5 б) пунктирным ребром. На рис.6.5 в) показано дерево полного префиксного кода. В данном случае вершины, соответствующие словам префиксного кода, как бы "разрезают" словарный универсум на две части - "верхнюю" и "нижнюю". Если попытаться добавить слово "выше" кодовых слов, то одно из кодовых слов станет префиксом добавляемого слова. Если добавлять слово "ниже" слов префиксного кода, то добавляемое слово окажется префиксом одного из кодовых слов. В обоих случаях нарушается свойство префиксности. На рис.6.5 г) представлено дерево для рассмотренного ранее кода, не обладающего свойством префиксности. Таким образом, если свойство префикса не выполняется, то некоторые промежуточные вершины дерева могут соответствовать кодовым словам.
Замечание. Свойство префиксности является достаточным, но не является необходимым для однозначной декодируемости.
Пример. Код, состоящий из двоичных кодовых слов 1, 10, - не префиксный, но может быть однозначно декодирован. Появление символа 1 означает начало нового кодового слова. Последнее остается справедливым для кода, каждое слово которого есть единица с последующими нулями. Разумеется, подобные коды далеко не самые экономные.
Если код префиксный, то, читая кодовую запись подряд от начала, мы всегда сможем разобраться, где кончается одно кодовое слово и начинается следующее. Если, например, в кодовой записи встретилось кодовое обозначение 110, то разночтений быть не может, так как в силу префиксности наш код не содержит кодовых обозначений 1, 11 или, скажем, 1101. Именно так обстояло дело для рассмотренного выше кода, который очевидно является префиксным.