Теория языков
В этой лекции рассматриваются следующие темы:
- Различные способы задания языков в компиляции:
- Грамматики
- Конечные и магазинные автоматы
- Соотношения между различными способами задания языков
- Приложения этой теории в компиляции
Задача определения языка
Одна из первых задач, возникающих в процессе компиляции - это определение рассматриваемого языка программирования. При рассмотрении языков, состоящих из конечного множества цепочек, проще всего явным образом перечислить все допустимые входные цепочки. Но что делать с языками, не вводящими никаких ограничений на длину входной цепочки? Для потенциально бесконечных языков нам потребуется ввести какой-то конструктивный способ описания, который позволит нам задать правила, описывающие порождаемый ими язык. Такое описание должно удовлетворять некоторым свойствам:
- Само описание должно иметь конечную длину
- Для данного описания языка должен существовать алгоритм, который мог бы проверить принадлежность некоторой входной цепочки языку
Существует целый ряд математических формализмов, в той или иной степени удобных для задания языков - вообще, этап анализа входной программы наиболее разработан и лучше всего поддержан математическими теориями. Наиболее распространенным механизмом являются грамматики, которые задают все подходящие цепочки языка с помощью некоторых порождающих правил. Очевидное достоинство грамматик заключается в том, что существует множество систем, которые по заданной грамматике генерируют программу, проверяющую соответствие входной цепочки определяемому языку. Более того, полезную работу синтаксического анализатора (например, построение дерева разбора) можно проводить параллельно с самим распознаванием языка.
Другая часто используемая идея заключается в том, что создается некоторый обобщенный алгоритм, проверяющий за конечное число шагов принадлежность данной цепочки языку. Такой алгоритм либо останавливается после конечного числа шагов и говорит "да", либо останавливается и говорит "нет". Теоретически, нас могло бы устроить и зацикливание алгоритма на неподходящих входных цепочках, но на практике такое поведение не совсем удобно.
Определение грамматики
Грамматики представляют собой наиболее распространенный класс описаний языков. При описании грамматики необходимо начать с определения алфавита языка, который задается как набор допустимых терминальных символов. Кроме того, необходимо определить набор правил вывода вида  , с помощью которых строятся все цепочки языка. В левой и правой части этих правил могут встречаться специальные нетерминальные символы; в процессе вывода нетерминальные символы заменяются с помощью соответствующих правил до полной замены на соотвествующие терминалы. Наконец, грамматика должна включать в себя начальный символ , или аксиому, с которой начинается получение любого предложения языка.
, с помощью которых строятся все цепочки языка. В левой и правой части этих правил могут встречаться специальные нетерминальные символы; в процессе вывода нетерминальные символы заменяются с помощью соответствующих правил до полной замены на соотвествующие терминалы. Наконец, грамматика должна включать в себя начальный символ , или аксиому, с которой начинается получение любого предложения языка.
Для формального определения грамматики нам потребуются следующие обозначения. Если  есть алфавит, то
есть алфавит, то 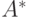 обозначает множество всех строк (включая пустую строку
обозначает множество всех строк (включая пустую строку  ), составленных из символов, входящих в
), составленных из символов, входящих в  . Аналогично,
. Аналогично, 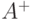 определяет множество всех строк, составленных из символов, входящих в
определяет множество всех строк, составленных из символов, входящих в  , но без пустой строки. Нетерминалы мы будем обозначать прописными буквами, а терминалы - строчными.
, но без пустой строки. Нетерминалы мы будем обозначать прописными буквами, а терминалы - строчными.
Итак, грамматика  определяется как следующая четверка:
определяется как следующая четверка: 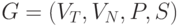 , где
, где
-
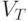 - конечное множество терминальных символов;
- конечное множество терминальных символов; -
 - не пересекающееся с
- не пересекающееся с 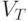 конечное множество нетерминальных символов;
конечное множество нетерминальных символов; -
 - конечный набор порождающих правил вида (
- конечный набор порождающих правил вида (  ,
, 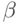 ), где
), где 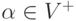 ,
, 
-
 - начальный символ, где
- начальный символ, где 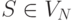
Например, грамматикой, порождающей язык 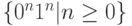 , является
, является 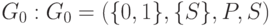 , где
, где  . Другой пример: рассмотрим грамматику, порождающую язык
. Другой пример: рассмотрим грамматику, порождающую язык 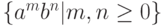 . Такая грамматика имеет вид
. Такая грамматика имеет вид  , где набор правил определяется следующим образом:
, где набор правил определяется следующим образом: 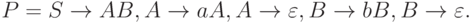
Определим также понятие выводимости: если  - цепочка, состоящая из символов языка
- цепочка, состоящая из символов языка  , а
, а 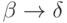 - правило языка
- правило языка  , то
, то  непосредственно выводима из
непосредственно выводима из 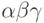 в G). Рефлексивное и транзитивное замыкание этого отношения обозначим как
в G). Рефлексивное и транзитивное замыкание этого отношения обозначим как  (цепочка
(цепочка  выводима из
выводима из  ; имя грамматики можно опускать для краткости).
; имя грамматики можно опускать для краткости).
