Теория языков

Некоторые свойства грамматик

Отметим некоторые свойства грамматик, которые нам придется учитывать в дальнейшем при построении грамматик реальных языков программирования.

Во-первых, различные грамматики могут порождать один и тот же язык (такие грамматики называются эквивалентными ). Например, приведенная выше грамматика эквивалентна следующей грамматике , где правила из P определены следующим образом: .

Несмотря на эквивалентность определяемых языков, одна грамматика может быть значительно удобнее другой с точки зрения ее использования в компиляторе. Поэтому в дальнейшем мы будем рассматривать некоторые приемы преобразования грамматик с целью улучшения удобства работы с языком.

Во-вторых, необходимо отметить, что определение грамматик не накладывает никаких ограничений на количество нетерминалов в левой части правил и приведенные выше примеры не должны создавать обманчивого впечатления, что все грамматики содержат один и только один нетерминал в левой части каждого правила. В качестве иллюстрации приведем следующий пример: 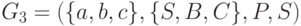, где содержит следующие правила: 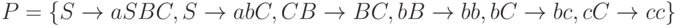. Это абсолютно законная грамматика, порождающая язык .

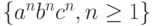В качестве другого примера приведем еще одну грамматику, эквивалентную грамматик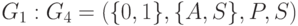е , где . В этом варианте левая часть одного из правил содержит пару из терминального и нетерминального символа.

В-третьих, упомянем одно соглашение, которое нам пригодится впоследствии: для обозначения n правил вида мы будем использовать следующую запись: 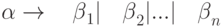. В правилах такого вида вертикальная черта читается как "или".

Иерархия Хомского

Итак, мы убедились, что существует множество различных видов грамматик и, предположительно, некоторые из них могут оказаться удобнее для наших целей. Поэтому мы введем классификацию грамматик согласно их внешнему виду (эта классификация известна как иерархия Хомского, по фамилии автора).

Грамматика называется:

• выровненной вправо (праволинейной) , если любое правило из имеет вид или , где , - нетерминалы, а - терминал (возможно, пустой).
• контекстно-свободной (бесконтекстной) , если любое правило из имеет вид , где - нетерминал, - нетерминал или терминал
• контекстно-зависимой (неукорачивающей) , если все правила из 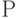имеют вид , где
• общего вида (без ограничений) , если грамматика не удовлетворяет ни одному из указанных выше ограничений.

Иногда приведенные выше классы нумеруют от трех до нуля и называют каждый класс "грамматикой типа n", например, грамматика общего вида называется грамматикой типа . Мы будем избегать этого обозначения, так как оно не проясняет суть вопроса.

Очевидно, что эта классификация - включающая, т.е. все контекстно-свободные грамматики являются и контекстно-зависимыми, все контекстно-зависимые грамматики являются грамматиками общего вида и т.д. Кроме того, можно показать, что существуют языки, принадлежащие к типу i, но не к типу i+1. Например, язык 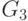является контекстно-зависимым, но не контекстно-свободным, т.е. не существует контекстно-свободной грамматики, порождающий этот язык. С другой стороны, некоторые нерегулярные грамматики могут порождать регулярные языки (например, грамматика - нерегулярная, но порождаемый ею язык регулярен, т.к. эквивалентная грамматика 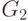регулярна). Наконец, отметим, что определение контекстно-зависимой грамматики запрещает использование правил вида . Это сделано для того, чтобы алгоритм, определяющий принадлежность цепочки языку, не мог бы зациклиться.