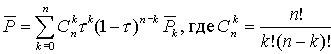Программное рисование во Flash MX
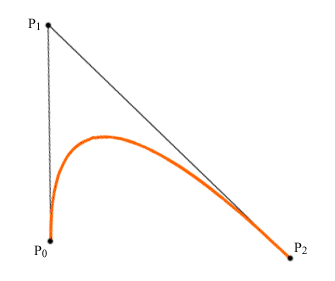
В References можно прочитать, что оператор curveTo рисует кривую, используя текущий стиль линии, начиная от текущей позиции и заканчивая в точке (xTarget, yTarget) (имена переменных взяты из примера 10.9), используя контрольную точку (xControl, yControl). Что означает эта контрольная точка, разработчики не конкретизируют, оставляя пользователю простор для догадок. Однако, с помощью несложного исследования можно установить, что curveTo изображает кусок параболы, начинающийся в текущей позиции и заканчивающийся в (xTarget, yTarget), такой что касательные в начальной и конечной точках пересекаются в точке (xControl, yControl).
Это так называемая кривая Безье второго порядка.
Кривая Безье представляет собой гладкую кривую, построенную по конечному набору точек на плоскости. Строится она следующим образом.

Для начала рассмотрим построение кривой Безье для трех точек.
Пусть на плоскости заданы три точки P0, P1 и P2. Для определенного значения параметра  от 0 до 1 выберем на отрезке [P0, P1] точку
от 0 до 1 выберем на отрезке [P0, P1] точку  , которая делит отрезок в отношении
, которая делит отрезок в отношении 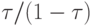 , на отрезке [P1, P2] - аналогичную точку
, на отрезке [P1, P2] - аналогичную точку 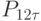 , и на получившемся отрезке
, и на получившемся отрезке ![[P_{01\tau}, P_{12\tau}]](/sites/default/files/tex_cache/058c63db80dfe7c079769aa8d3cb03b1.png) - точку
- точку 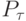 , которая в свою очередь делит отрезок
, которая в свою очередь делит отрезок ![[P_{01\tau}, P_{12\tau}]](/sites/default/files/tex_cache/058c63db80dfe7c079769aa8d3cb03b1.png) в отношении
в отношении  . Точки
. Точки 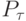 , полученные таким образом для всех значений
, полученные таким образом для всех значений  от 0 до 1, и составляют кривую Безье второго порядка.
от 0 до 1, и составляют кривую Безье второго порядка.
Нетрудно показать, что кривая 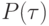 проходит через точки P0 и P2, касательные к ней в этих точках совпадают с прямыми, на которых лежат отрезки [P0, P1] и [P2, P1], это кривая второго порядка (парабола), аналитически в векторном виде записывается следующим образом:
проходит через точки P0 и P2, касательные к ней в этих точках совпадают с прямыми, на которых лежат отрезки [P0, P1] и [P2, P1], это кривая второго порядка (парабола), аналитически в векторном виде записывается следующим образом:
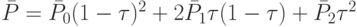 ,
, ![\tau \in [0,1]](/sites/default/files/tex_cache/d28eb35ae921ad45f4051eb61fe65837.png)
Способ построения кривой Безье для произвольного числа точек показан на рис. 10.6 (на примере шести точек P0 - P5 ). Так же, как и в рассмотренном выше случае трех точек, для каждого значения параметра  от 0 до 1 найдем соответствующую этому значению точку кривой (рис. 10.6а). Для этого сначала разделим каждый отрезок ломаной P0 - P5 в отношении
от 0 до 1 найдем соответствующую этому значению точку кривой (рис. 10.6а). Для этого сначала разделим каждый отрезок ломаной P0 - P5 в отношении  (рис. 10.6б). Далее, получившиеся пять точек (
(рис. 10.6б). Далее, получившиеся пять точек (  ,
, 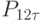 , и т.д., см. рис.) соединим отрезками, и каждый из них в свою очередь разделим в отношении
, и т.д., см. рис.) соединим отрезками, и каждый из них в свою очередь разделим в отношении  (рис. 10.6в). Будем повторять эту процедуру до тех пор, пока у нас не останется один отрезок
(рис. 10.6в). Будем повторять эту процедуру до тех пор, пока у нас не останется один отрезок  (рис. 10.6г). Точка, которая делит этот отрезок в отношении
(рис. 10.6г). Точка, которая делит этот отрезок в отношении  , и будет искомой точкой
, и будет искомой точкой 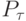 . Если изменять значения
. Если изменять значения  от 0 до 1 и для каждого находить точку таким образом, то мы получим кривую Безье n -го порядка, где n на 1 меньше числа точек (в данном случае порядок кривой будет пятый).
от 0 до 1 и для каждого находить точку таким образом, то мы получим кривую Безье n -го порядка, где n на 1 меньше числа точек (в данном случае порядок кривой будет пятый).
Можно доказать, что в аналитическом виде формула кривой Безье n -го порядка выглядит так:
Эта кривая представляет собой как бы сглаженный вариант ломаной P0...Pn. Можно выделить несколько полезных свойств кривых Безье. Так, эта кривая всегда проходит через точки P0 и Pn. Касательные к кривой в этих точках совпадают с направлениями отрезков [P0, P1] и [Pn-1, Pn] соответственно. Касательная в произвольной точке 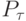 совпадает с направлением отрезка
совпадает с направлением отрезка ![[P_{0(n-1)\tau}, P_{1n\tau}]](/sites/default/files/tex_cache/53e2a69ecf6c8fdba013683882444948.png) . Часть кривой между точками P0 и
. Часть кривой между точками P0 и 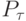 так же представляет собой кривую Безье n -ного порядка, построенную на точках
так же представляет собой кривую Безье n -ного порядка, построенную на точках ![[P_0, P_{01\tau}...P_{0(n-1)\tau}, P_\tau]](/sites/default/files/tex_cache/8be3619f82eef1ca0471c3eedb3d47ef.png) . Аналогично, ост
авшаяся часть кривой - между точками
. Аналогично, ост
авшаяся часть кривой - между точками 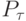 и Pn - тоже является кривой Безье n -ного порядка, построенной на точках
и Pn - тоже является кривой Безье n -ного порядка, построенной на точках ![[P_\tau, P_{1n \tau}...P_{(n-1)n}\tau, P_n]](/sites/default/files/tex_cache/537db04c1796c8609f19e7e5feadbc81.png) .
.
На практике кривые Безье применяют для упрощения построения произвольных кривых, даже не заданных аналитически. Чаще всего для этого используют кривые Безье третьего порядка, так называемые кубические сплайны. Они достаточно просты для вычислений, но с их помощью уже можно с хорошей точностью приблизить любую гладкую кривую. Благодаря этому кривые Безье третьего порядка получили широкое распространение в компьютерной графике: их можно встретить практически в любом редакторе, позволяющем работать с векторными изображениями. В том числе в редакторе Flash MX.
Как нетрудно догадаться, для построения кривой Безье третьего порядка нужны четыре точки. Две точки задают начало и конец кривой (назовем их опорными), а две другие - направления касательных в опорных точках, их будем называть контрольными.
Уравнение кривой Безье третьего порядка выглядит так:
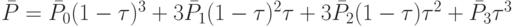 ,
,
где  - точка на кривой,
- точка на кривой, 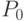 и
и  - опорные точки,
- опорные точки,  и
и  - контрольные точки,
- контрольные точки,  - параметр, пробегающий значения от 0 до 1. Это уравнение можно также переписать в виде
- параметр, пробегающий значения от 0 до 1. Это уравнение можно также переписать в виде
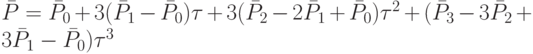
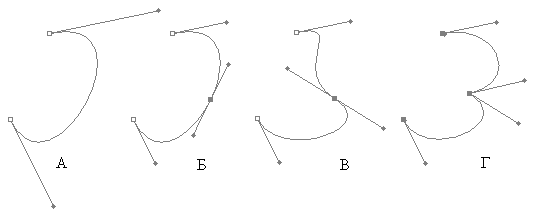
В редакторах векторной графики пользователь имеет возможность передвигать опорные и контрольные точки, а также добавлять на кривую новые опорные точки (рис. 10.7)
При добавлении новой точки кривая разбивается на две, но в первый момент это никак не влияет на ее форму (рис. 10.7 Б). Однако получившиеся кривые можно редактировать независимо, и после редактирования они уже не могут быть преобразованы обратно в одну кривую Безье (рис. 10.7 Б и В). Тем не менее, кривая в этом случае может остаться непрерывной и даже гладкой - если редактировать контрольные точки так, что на стыке двух участков опорная точка и две контрольные оставались на одной прямой (см. рис. 10.7 В), - она и будет касательной к кривой в данной точке (гладкость C1 ).
А) Кривая Безье третьего порядка
Б) Та же кривая, разбитая на две части. Обратите внимание, что контрольные точки на концах исходной кривой стали ближе к соответствующим опорным, хотя вид кривой не изменился - дело в том, что они управляют уже не целой кривой, а только ее частью
В) Редактирование отдельных частей кривой с сохранением гладкости в точке соединения
Г) Редактирование двух частей кривой независимо друг от друга.
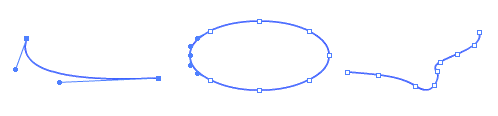
Кривые, нарисованные в редакторе Flash MX, тоже представляют собой набор кубических сплайнов. Опорные точки в них расставляются автоматически (рис. 10.8).
Как уже отмечалось, кубическими сплайнами можно аппроксимировать кривую любой сложности. Однако, напомним, что оператор curveTo рисует кривую Безье второго порядка. Эта кривая гораздо проще, чем кубический сплайн, и для аппроксимации произвольных линий таких кривых понадобилось бы больше.
Так, например, для построения окружности (или эллипса) с хорошей точностью достаточно четырех кубических сплайнов, а квадратичных надо как минимум 10-12 (см. рис. 10.9).
На рисунке 10.9 эллипс - светло-серая кривая - практически невозможно отличить от кубического сплайна (тонкая черная кривая), построенного по точкам A, 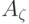 ,
, 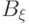 и B. Контрольные точки
и B. Контрольные точки 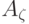 и
и 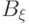 подбирались так, чтобы в точках A и B совпадали радиусы кривизны сплайна и исходной кривой (эллипса). Радиус кривизны кривой вычисляется по формуле
подбирались так, чтобы в точках A и B совпадали радиусы кривизны сплайна и исходной кривой (эллипса). Радиус кривизны кривой вычисляется по формуле
где точкой обозначается дифференцирование по параметру. Для эллипса
R(A) = b2/a, R(A) = a2/b.
Такими же будут радиусы кривизны в этих точках и для кубического сплайна, если взять
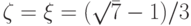 .
.