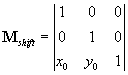Программное рисование во Flash MX
Сплошные и градиентные заливки
Кроме линий, во Флэш МХ есть возможность рисовать и протяженные области, залитые одним цветом или градиентом. Для этого есть методы beginFill, beginGradientFill и endFill.
Рассмотрим сначала сплошную заливку. Она делается при помощи методов beginFill и endFill, между вызовами которых с помощью операторов lineTo и curveTo рисуется ограничивающий контур (см. пример 10.10)
(строки примера пронумерованы, но номера, естественно, не являются частью кода).
1. _root.createEmptyMovieClip("fill_mc", 1);
2.
3. fill_mc.lineStyle(2, 0x9900ff, 100);
4.
5. fill_mc.beginFill(0xccccff, 100);
6. fill_mc.moveTo(50, 50);
7. fill_mc.lineTo(75, 0);
8. fill_mc.lineTo(100, 50);
9. fill_mc.lineTo(75, 100);
10. fill_mc.lineTo(50, 50);
11. fill_mc.endFill();
12. //--------------
10.10.
Первый аргумент beginFill - цвет заливки (в примере 10.10 0xccccff, светло-фиолетовый), второй - прозрачность заливки (меняется от 0 до 100, 0 - полностью прозрачный, 100, как в примере 10.10 - полностью непрозрачный).
Здесь следует обратить внимание на несколько вещей. Во-первых, линия, нарисованная между вызовами beginFill и endFill должна быть непрерывной. То есть, оператор moveTo может быть вызван только один раз, в начале. Если он встречается несколько раз, то закрашена будет только область, нарисованная между последним вызовом moveTo и вызовом endFill. Если конечная позиция контура не совпадает с начальной (если бы в примере 10.10 не было строчки 10), то при вызове оператора endFill контур замыкается прямой линией на начальную позицию (последний вызов moveTo ).
Это документированное поведение операторов beginFill и endFill. Однако при некоторых условиях результат их выполнения может оказаться непредсказуемым. (В частности, результат заливки может зависеть от предыстории - от того, что делалось в этом клипе до вызова beginFill. Например, если там не встречалось ни одного оператора moveTo, заливка может лишь отдаленно напоминать то, что вы ожидаете получить.) Чтобы заливка работала устойчиво, нужно поступать следующим образом. Во-первых, с помощью moveTo перенести текущую позицию в начало контура до того, как будет вызван beginFill, во-вторых, конечная позиция контура должна совпадать с начальной.
Между beginFill и endFill может быть вызван метод lineStyle - если нужно разные части контура рисовать разным стилем. Если нужна заливка без контура, можно вызвать lineStyle без аргументов.
FlashMX позволяет делать заливки не только сплошным цветом, но и с плавным изменением цвета и прозрачности (градиентом). Для этого существует метод beginGradientFill.
Все, что до сих пор было сказано про beginFill (кроме описания аргументов), справедливо и для beginGradientFill. На аргументах beginGradientFill остановимся подробнее.
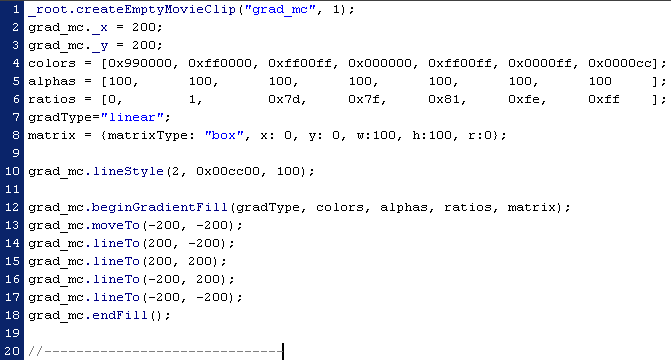
Часть примера показана в виде скриншота, чтобы сохранить нумерацию строк.
1. _root.createEmptyMovieClip("grad_mc", 1);
2. grad_mc._x = 200;
3. grad_mc._y = 200;
4. colors = [0x990000, 0xff0000, 0xff00ff, 0x000000, 0xff00ff, 0x0000ff, 0x0000cc];
5. alphas = [100, 100, 100, 100, 100, 100, 100 ];
6. ratios = [0, 1, 0x7d, 0x7f, 0x81, 0xfe, 0xff ];
7. gradType="linear";
8. matrix = {matrixType: "box", x: 0, y: 0, w:100, h:100, r:0};
9.
10. grad_mc.lineStyle(2, 0x00cc00, 100);
11.
12. grad_mc.beginGradientFill(gradType, colors, alphas, ratios, matrix);
13. grad_mc.moveTo(-200, -200);
14. grad_mc.lineTo(200, -200);
15. grad_mc.lineTo(200, 200);
16. grad_mc.lineTo(-200, 200);
17. grad_mc.lineTo(-200, -200);
18. grad_mc.endFill();
19.
20. //---------------
10.11.
В результате выполнения этого кода будет нарисован квадрат 400*400 (его контур обозначен в строчках 13-17), часть которого будет представлять собой плавный переход одного цвета в другой. Эти цвета и переход между ними определяются аргументами метода beginGradientFill (строчка 12).
Первый аргумент, gradType (определен в строке 7) - тип градиента, представляет собой строчку " linear " или " radial ". В первом случае области одинакового цвета будут представлять собой параллельные линии, во втором - эллипсы с одним центром.
Второй аргумент, colors, представляет собой массив, члены которого - ключевые цвета градиента. Цвета, которые находятся между ними, рассчитываются так, чтобы переход между ключевыми был линейным.
Третий аргумент, alphas, - массив прозрачностей ключевых цветов из массива colors. Длины этих массивов должны совпадать.
Четвертый, ratios, - относительные положения ключевых цветов градиента. Длина этого массива должна совпадать с длиной массивов colors и alphas. Каждый элемент массива places представляет собой число от 0 до 0xff. Если ratios[i]==0, то цвет, соответствующий colors[i] будет располагаться слева в случае градиента типа " linear " и в центре в случае " radial ". 0xff соответствует правому краю и границе эллипса соответственно. Иными словами, компонент цвета сj (R, G или B) зависит от относительного положения r следующим образом:
cj(r) = colors[i]j + (r - ratios[i]j)((colors[i + 1]j + colors[i]j)/(ratios[i + 1]j + ratios[i]j)), ratios[i] <= r < ratios[i + 1] (10.1)
(В формуле 10.1 под colors[i]j понимается компонент цвета colors[i], R, G или B, соответствующий cj ). Аналогичное выражение можно получить и для прозрачности 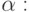
![\alpha (r) = alphas[i] + (r - ratios[i])((alphas[i + 1] + alphas[i])/(ratios[i + 1] + ratios[i])), ratios[i] <= r < ratios[i + 1] (10.2)](/sites/default/files/tex_cache/a443a041695812839c94fdaba64047ed.png)
Чтобы результат выполнения операции beginGradientFill был предсказуемым, значения в массиве ratios должны быть монотонны. Контролировать процесс удобнее, если ratios[0] равно 0, а последний элемент в этом массиве равен 0xff, однако это не обязательно: в противном случае градиент просто дополняется соответственно первым и последним элементами массивов colors и alphas. К сожалению, на три перечисленных массива есть одно недокументированное ограничение: их длина не может быть больше 8. Точнее, может, но учитываются все равно только первые 8 элементов (с номерами от нулевого по седьмой включительно). Напомним также про необходимость делать все три массива одинаковой длины.
В примере 10.11 ratios специально подобраны так, чтобы было видно, где кончается градиент и начинается сплошной цвет (переход между 0 и 1, а так же между 0xfe и 0xff выглядит как резкая граница), а кроме того, в центре присутствует четкая черная полоска.
И, наконец, аргумент matrix. Он задает расположение градиента на экране относительно локальных координат клипа. Остановимся на нем подробнее.
matrix - матрица трансформации - представляет собой объект, который должен содержать либо поля {a, b, c, d, e, f, g, h, i}, либо {matrixType, w, h, x, y, r} , как в примере 10.11.
Рассмотрим первый вариант. В этом случае поля объекта matrix рассматриваются как матрица 3x3
которая используется следующим образом.
Предположим, что зависимость компонентов цвета и прозрачности от координат выражается функциями cj = fj(x, y), 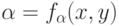 . Так как cj и
. Так как cj и  зависят только от относительного положения r, то достаточно рассмотреть только функцию
зависят только от относительного положения r, то достаточно рассмотреть только функцию
r = f (x, y) (10.4)
В случае градиента типа " linear " функция 10.4 принимает вид
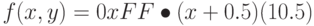
То есть, от y цвет не зависит, а от x зависит линейно, при х = -0.5 r = 0, при x = 0.5 r = 0xff, так что весь градиент занимает вертикальную полоску шириной 1.
Если градиент имеет тип " radial ", то функция 10.4 выглядит так:

В этом случае r=0 соответствует точке (0, 0), а r = 0xFF - окружности x2 + y2 = 0.25, то есть весть градиент занимает круг с центром (0, 0) и диаметром 1.
С практической точки зрения эти функции все еще бессмысленны - никому не нужен градиент, умещающийся в 1 пиксель.
Преобразуем функцию 10.4 с помощью матрицы 10.3. Эта матрица описывает такое преобразование f->fM, что обратное к нему fM->f можно записать через коэффициенты матрицы следующим образом:
f (x, y) = fM(ax + dy + g,bx + ey + h) (10.7)
(Здесь реальные экранные координаты - это x = ax + dy + g,y = bx + ey + h, а x и y - аргументы функции 10.5 или 10.6.)
Функция fnof;M в 10.7 уже задает градиент любого размера и расположения на экране.
Обратите внимание, что параметры c, f и i в преобразовании 10.7 не используется. Предполагается, что их значения не меняются: c = 0, f = 0 и i = 1. То есть, матрица 10.3 на самом деле выглядит так:
В References написано, что в аргументе в объекте matrix должны присутствовать все 9 параметров, в том числе c, f и i. Однако их значения (и даже их наличие или отсутствие) на вид градиента никак не влияют. Возникает естественный вопрос: если значения этих параметров ни на что не влияют, зачем вообще о них говорить? В ответ можно привести следующее рассуждение. Предположим, что функция f определена не в двумерном, а в трехмерном пространстве. Тогда преобразование 10.7 выглядело бы так:
f'(x, y, z) = f'M(ax + dy + gz, bx + ey + hz, cz + fy + iz) (10.9)
То есть, просто представляло бы собой умножение вектора аргументов (x, y, z) на матрицу 10.3. Формула 10.7 получается из 10.9, если положить 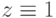 . Еще одна причина, чтобы говорить об аргументе matrix как о матрице 3x3, - это удобство выполнения последовательных преобразований. Так, для того, чтобы получить матрицу преобразования, которое получается последовательным выполнением двух преобразований с матрицами M1 и M2, нужно просто перемножить эти матрицы.
. Еще одна причина, чтобы говорить об аргументе matrix как о матрице 3x3, - это удобство выполнения последовательных преобразований. Так, для того, чтобы получить матрицу преобразования, которое получается последовательным выполнением двух преобразований с матрицами M1 и M2, нужно просто перемножить эти матрицы.
Из 10.10 нетрудно получить, что если матрицы M1 и M2 имеют вид 10.8, то матрица M тоже имеет вид 10.8:
Не забывайте: важно, в каком порядке выполняются преобразования; в данном случае сначала M2 потом M1 (это справедливо постольку, поскольку мы имеем дело с обратным преобразованием fM -> f. Если бы преобразование было прямым, то запись 10.11 означала бы, что выполняется сначала M1 потом M2 ).
Связь между компонентами матрицы 10.3 и параметрами градиента на первый взгляд кажется неочевидной. Чтобы это прояснить, рассмотрим несколько примеров.
Тогда преобразование градиента будет  , то есть
, то есть
 в случае градиента " linear "
в случае градиента " linear "
Таким образом, градиент просто растягивается в ширину на W и в высоту на H пикселей.
Чтобы проверить, как это будет выглядеть на экране, можно воспользоваться следующим примером:
_root.createEmptyMovieClip("grad_mc", 1);
grad_mc._x = 200;
grad_mc._y = 200;
colors = [0xffffff, 0x000000, 0xffffff, 0x000000, 0xffffff, 0xcccccc, 0xffffff];
alphas = [100, 100, 100, 100, 100, 100, 100 ];
ratios = [0, 1, 0x7d, 0x7f, 0x81, 0xfe, 0xff ];
//Задаем компоненты матрицы.
//Чтобы задать новую матрицу, достаточно будет изменить эти строчки.
a0 = 100; b0 = 0;
d0 = 0; e0 = 50;
g0 = 0; h0 = 0;
//-------------
gradType="radial"; //Задаем тип градиента
// Создаем матрицу
matrix = {a: _root.a0, b: _root.b0,
d: _root.d0, e: _root.e0,
g: _root.g0, h: _root.h0}
grad_mc.clear();
grad_mc.lineStyle(2, 0x00cc00, 100);
//Рисуем заливку градиентом
grad_mc.beginGradientFill(gradType, colors, alphas, ratios, matrix);
grad_mc.moveTo(-200, -200);
grad_mc.lineTo( 200, -200);
grad_mc.lineTo( 200, 200);
grad_mc.lineTo(-200, 200);
grad_mc.lineTo(-200, -200);
grad_mc.endFill();
//------------
// Кроме градиента нарисуем еще вспомогательный четырехугольник,
// в который превращается квадрат [-0.5<x<0.5, -0.5<y<0.5]
// после преобразования,задаваемого матрицей matrix.
with (matrix){
grad_mc.lineStyle(0, 0x808080, 100);
grad_mc.moveTo(0.5*(-a - d) + g, 0.5*(-b - e) + h);
grad_mc.lineTo(0.5*(-a + d) + g, 0.5*(-b + e) + h);
grad_mc.lineTo(0.5*( a + d) + g, 0.5*( b + e) + h);
grad_mc.lineTo(0.5*( a - d) + g, 0.5*( b - e) + h);
grad_mc.lineTo(0.5*(-a - d) + g, 0.5*(-b - e) + h);
}
10.12.
Результат применения матрицы 10.12 ( W = 100, H = 50 ) для линейного и радиального градиентов (код приведен в примере 10.12).
Для поворота градиента на угол по часовой стрелке служит матрица следующего вида:
Матрица последовательного выполнения масштабирования и поворота будет выглядеть так:
Результат применения матрицы 10.14 ( W = 100, H = 50, 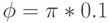 ) для линейного и радиального градиентов.
) для линейного и радиального градиентов.
Поворот и масштабирование оставляют на месте центр градиента. Переместить этот центр затем можно с помощью матрицы следующего вида:
Для выполнения масштабирования, поворота и смещения служит матрица
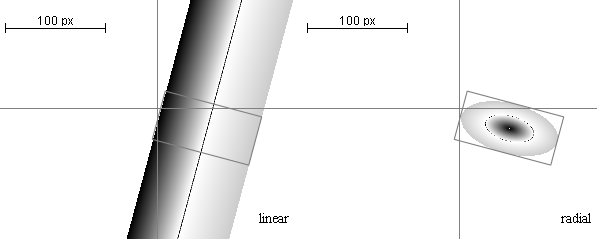
Результат применения матрицы 10.16 ( W = 100, H = 50, 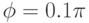 , x0 = 50, y0 = 20 ) для линейного и радиального градиентов.
, x0 = 50, y0 = 20 ) для линейного и радиального градиентов.
Матрица вида 10.16 наиболее очевидно и естественно описывает любое возможное расположение градиента. Это градиент, умещающийся в прямоугольник высотой H и шириной W, повернутый по часовой стрелке на угол  с центром в точке (x0, y0). Никакого более сложного градиента на Flash МХ сделать невозможно.
с центром в точке (x0, y0). Никакого более сложного градиента на Flash МХ сделать невозможно.
Если приглядеться к матрице 10.16 повнимательнее, можно заметить, что там используется только 5 независимых параметров: W, H, x0, y0, и 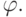 Однако в объекте matrix, который является аргументом метода beginGradientFill, их может быть шесть. Действительно, преобразование 10.16 оставляет исходный квадрат [-0.5 < x < 0.5, -0.5 < y < 0.5] прямоугольником, а в общем же случае он становится параллелограммом. Тем не менее к противоречию с тем, что сказано выше, это не приводит. В этом легко убедиться, если для произвольной матрицы вида 10.8 подобрать матрицу вида 10.16 с параметрами
Однако в объекте matrix, который является аргументом метода beginGradientFill, их может быть шесть. Действительно, преобразование 10.16 оставляет исходный квадрат [-0.5 < x < 0.5, -0.5 < y < 0.5] прямоугольником, а в общем же случае он становится параллелограммом. Тем не менее к противоречию с тем, что сказано выше, это не приводит. В этом легко убедиться, если для произвольной матрицы вида 10.8 подобрать матрицу вида 10.16 с параметрами
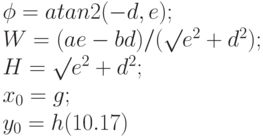
для линейного градиента, и с параметрами

где
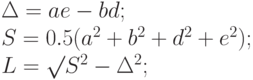
для радиального. Градиент, построенный по этой матрице, будет идентичен исходному. Проверить это можно, слегка изменив код из примера 10.12:
matrix = {a: _root.a0, b: _root.b0,
d: _root.d0, e: _root.e0,
g: _root.g0, h: _root.h0}
with (matrix){
_root.delta = a*e - b*d;
if (gradType == "radial"){
S=0.5*(e*e + a*a + d*d + b*b);
L=Math.sqrt(S*S-delta*delta);
h1 = delta / Math.sqrt(L + S);
w1 = delta / Math.sqrt(S - L);
phi1 = 0.5*Math.atan2( 2*(e*d + a*b), d*d + a*a - e*e - b*b );
} else {
h1=Math.sqrt(e*e + d*d);
w1=delta/h1;
phi1=Math.atan2(-d, e);
}
}
matrix1 = {a: w1*Math.cos(phi1), b: w1*Math.sin(phi1),
d:-h1*Math.sin(phi1), e: h1*Math.cos(phi1),
g: _root.g0, h: _root.h0}
grad_mc.beginGradientFill(gradType, colors, alphas, ratios, matrix1);
grad_mc.moveTo(-200, -200);
grad_mc.lineTo( 200, -200);
grad_mc.lineTo( 200, 200);
grad_mc.lineTo(-200, 200);
grad_mc.lineTo(-200, -200);
grad_mc.endFill();
with (matrix){
grad_mc.lineStyle(0, 0x808080, 100);
grad_mc.moveTo(0.5*(-a - d) + g, 0.5*(-b - e) + h);
grad_mc.lineTo(0.5*(-a + d) + g, 0.5*(-b + e) + h);
grad_mc.lineTo(0.5*( a + d) + g, 0.5*( b + e) + h);
grad_mc.lineTo(0.5*( a - d) + g, 0.5*( b - e) + h);
grad_mc.lineTo(0.5*(-a - d) + g, 0.5*(-b - e) + h);
}
10.13.
В этом примере градиент строится по матрице matrix1 вида 10.16, а ограничивающий прямоугольник - по исходной матрице matrix. Нетрудно убедиться, что градиент оказывается вписанным в четырехугольник при любых параметрах исходной матрицы.



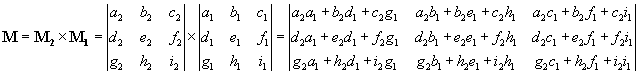
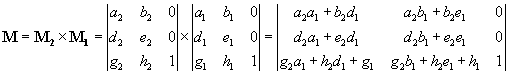

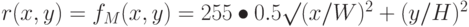 в случае "
в случае "