Основы векторной графики. Базовые принципы работы в CorelDRAW
Графика растровая и векторная. Плюсы и минусы векторной графики
Форматов для хранения изображений на компьютере два: растровый и векторный. В векторном формате изображение описывается как совокупность отдельных объектов, заданных математически (формулами), а в растровом - по точкам (как мозаика). Например, чтобы описать отрезок прямой в векторном формате необходимо задать координаты начала и конца прямой, ее цвет и толщину. Для описания той же прямой в растровом формате задаются координаты каждой ее точки и цвет точек.
Для эффективного применения векторной графики в творческой работе необходимо представлять себе ее достоинства и недостатки.
Векторный формат более компактный, но он не пригоден для хранения реалистичных изображений, например фотографий. В этом формате задавать их математически сложно и громоздко, а поэтому - нерационально. А вот рисунки и чертежи удобно и целесообразно создавать и хранить именно в векторном виде.
Достоинствами векторных изображений является следующее:
- увеличение масштаба происходит без потери качества изображений;
- небольшой размер файла по сравнению с растровыми изображениями;
- прекрасное качество вывода векторных изображений на печать;
- возможность редактирования каждого элемента изображения в отдельности;
- векторным программам свойственна высокая точность рисования (до сотой доли микрона);
- векторная графика экономна в плане объемов дискового пространства, необходимого для хранения изображений. Это связано с тем, что сохраняется не само изображение, а только некоторые основные данные (математическая формула объекта), используя которые программа всякий раз воссоздает изображение заново.
Недостатки векторного формата:
- сложность преобразования (трассировки) из растрового формата в векторный;
- векторная графика ограничена в чисто живописных средствах и не позволяет получать фотореалистичные изображения с тем же качеством, что и растровая. Причина в том, что здесь, в отличие от растровой графики, минимальной областью, закрашиваемой однородным цветом, является не один пиксел, а один объект. А размеры объекта по определению больше;
- невозможно применение обширной библиотеки эффектов (фильтров), используемых при работе с растровыми изображениями;
- сложность для понимания окружающего нас мира в виде векторов начинающими пользователями. Попробуйте описать, например, утро в осеннем лесу математическими формулами;
- аппаратные средства для работы с векторными рисунками (каттеры, плоттеры) более сложны и дороги, чем "железо" в растровой графике (мониторы, сканеры).
Строго говоря, ни один современный профессиональный графический пакет не является чисто векторным или чисто растровым, а совмещает в себе элементы как того, так и другого вида графики.
Что же такое "вектор"?
Для понимания термина "вектор" стоит вспомнить школьный курс физики. Там, было понятия понятие точки и приложенной к ней силы. Точка - это то место, куда сила прикладывается. А приложенная в точке сила характеризуется ее величиной и направлением. В компьютерной графике две связанные между собой точки, к каждой из которых приложена какая-либо сила в каком-либо направлении, могут сформировать некую линию, которая по своей форме будет соответствовать исходным параметрам каждой из этих точек. Сказанное нами графически можно изобразить так, как показано на рис. 2.1.
Объектов и явлений, которые можно описать с помощью векторных величин, чрезвычайно много и не только в курсе физики, но и в нашей повседневной жизни. А что касайтся цифровой графики, то здесь любую сложную кривую можно разбить на маленькие отрезки, форму которых можно определить всего парой точек и дугой между ними.
Изображение, созданное в векторных программах, основывается на математических формулах, а не на координатах пикселов. Поэтому векторные файлы содержат наборы инструкций для построения геометрических объектов - линий, эллипсов, прямоугольников, многоугольников и дуг. В соответствии с этим основу векторных изображений составляют разнообразные линии или кривые, называемые векторами или, по-другому, контурами. Каждый контур представляет собой независимый объект, который можно редактировать: перемещать, масштабировать, изменять. В соответствии с этим векторную графику часто называют также объектно-ориентированной графикой.
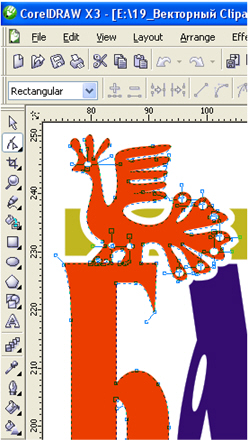
А вот таким образом выглядят векторы в рабочем пространстве программы CorelDRAW ( рис. 2.2).
На этом фрагменте изображения легко увидеть отдельные точки (которые на языке этой программы называются "узлами") и линии, образованные векторами. Обратите внимание: на панели инструментов активизирован инструмент программы, предназначенный для работы с узлами и векторами. Называется он Shape Tool (Форма)1Здесь мы еще раз отметим, почему мы выбрали для изучения именно английскую, а не русскоязычную версию CorelDRAW. В оригинальной версии все инструменты названы однозначно. В локализованной версии один и тот же инструмент называется по-разному. Так, инструмент Shape Tool переводится как Фигуры, Произвольная фигура, Редактирование объекта и так далее. .
Итак, как видим, в векторном редакторе любой контур состоит из отдельных узлов и линий между ними. Умение работать с узлами является залогом успешного рисования объектов в CorelDRAW.
Узлы (Опорные точки)
Наряду с линией, другим основным элементом векторной графики является узел (опорная точка). Линии и узлы используются для построения контуров (векторов), которые могут быть представлены в виде прямой, кривой или формы. Каждый контур имеет несколько узлов. В векторных редакторах форму контура изменяют путем манипуляции узлами. Это можно сделать одним из следующих способов:
- перемещением узлов;
- изменением свойств узлов (атрибутов связанных с ними касательных линий и управляющих точек);
- добавлением или удалением узлов.
Таким образом, в основе всех процедур, связанных с редактированием (отчасти и созданием) любого типа контуров, лежит работа с узлами.
Касательные линии и управляющие точки на кривых Безье
Математик Пьер Безье (Pierre Bezier) открыл, что произвольную кривую можно задать с помощью двух векторов, находящихся в начале и конце кривой. Это положение легло в основу описания кривых Безье в CorelDRAW. Из множества кривых Безье можно составить любую кривую. Кроме положения начальной и конечной точки (то есть узлов кривой), внешний вид кривой определяется кривизной, то есть ее изогнутостью между двумя узлами. Кривизна определяется двумя параметрами кривой в каждом узле, которые графически представлены с помощью отрезков, выходящих из узлов. Эти отрезки называются манипуляторами кривизны. Степень кривизны определяется длиной манипулятора кривизны. Если манипуляторы кривизны с обеих сторон сегмента имеют нулевую длину, то сегмент будет прямым. Увеличение длины манипулятора кривизны превратит сегмент в кривую.
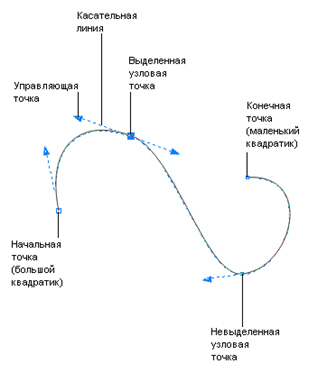
Итак, координаты узлов, наклон и длина манипуляторов кривизны определяют внешний вид кривой Безье. При выделении узловой точки криволинейного сегмента у нее появляются одна или две управляющие точки, соединенные с узловой точкой касательными линиями. Управляющие точки изображаются наконечниками стрелок. Расположение касательных линий и управляющих точек определяет длину и форму (кривизну) криволинейного сегмента, а их перемещение приводит к изменению формы контура ( рис. 2.3).
Наряду с термином "касательные" используются и другие термины: "рычаги управления" или "усы". Форма и цвет управляющих точек также зависят от вида используемого вами графического редактора. В CorelDRAW узловые и управляющие точки можно перемещать с помощью инструмента Shape (Форма).
Типы узловых точек
Вид касательных линий и соответственно методы управления кривизной сегмента в точке привязки определяются типом узловой точки. Различают три типа узловых точек:
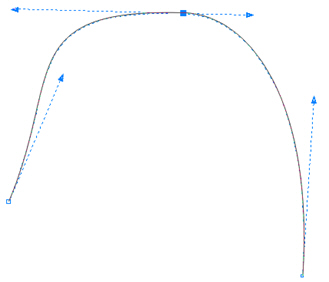
- гладкий узел (smooth node) - рис. 2.4;
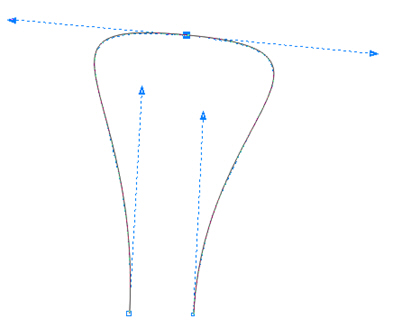
- симметричный узел (symmetrical node) - рис. 2.5;
- острый узел (cusp node).
У гладкой узловой точки касательные линии лежат на одной прямой, но имеют разную длину. Это говорит о том, что кривизна криволинейных участков, прилегающих к этой опорной точке, различна с разных ее сторон.
У симметричного узла оба отрезка касательных по обе стороны точки привязки имеют одинаковую длину и лежат на одной прямой, которая показывает направление касательной к контуру в данной узловой точке. Это означает, что кривизна сегментов с обеих сторон точки привязки одинакова. Этот тип узлов является частным случаем гладких узлов.
У острого узла касательные линии с разных сторон этой точки не лежат на одной прямой. Поэтому два криволинейных сегмента, прилегающих к опорной точке, имеют различную кривизну с разных сторон узловой точки и контур в этой точке образует резкий излом. В частности, один из отрезков касательных может быть равен нулю. В этом случае форма сегмента кривой будет регулироваться только одним отрезком касательной.