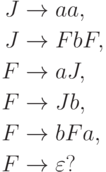НОУ ИНТУИТ | Математическая теория формальных языков. Лекция 16: Алгоритмически разрешимые проблемы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 09.07.2007 | Доступ: свободный | Студентов: 4 / 3 | Оценка: 4.56 / 4.26 | Длительность: 20:40:00

ISBN: 978-5-9556-0062-8

Темы: Программирование, Алгоритмы и дискретные структуры, Математика

Специальности: Математик

Теги: beta, finite, grammar, xml, автоматы, анализ, булева формула, дерево вывода, контекстно-свободная грамматика, контекстно-свободный язык, метка перехода, моноид, нетерминальный символ, протоколы, регулярные выражения, теория, шаг индукции, элементы

|

Вам нравится? Нравится 34 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В данной лекции рассматриваются наиболее известные разрешимые проблемы, связанные с грамматиками, автоматами и регулярными выражениями. Сформулированы также теоремы о разрешимости для некоторых алгоритмических проблем. Приведены практические примеры и упражнения для самостоятельного решения

Ключевые слова: контекстно-свободная грамматика, bounded automaton, операция дополнения, нетерминальный символ, всюду определенные функции, polynomial time, np-complete, булева формула, конъюнктивная нормальная форма, элементарная дизъюнкция, истинностное значение

В этой лекции рассматриваются наиболее известные разрешимые проблемы, связанные с грамматиками, автоматами и регулярными выражениями. Поскольку все приведенные выше доказательства эквивалентности разных способов конечного задания формального языка были конструктивными, не важно, какой из эквивалентных способов задания языка (например, посредством контекстно-свободной грамматики или автомата с магазинной памятью) используется в точной формулировке массовой задачи.

Первые два раздела этой лекции посвящены контекстным языкам. В разделах 15.3-15.6 сформулированы теоремы о разрешимости для некоторых алгоритмических проблем. Доказательства этих теорем опираются на конструктивность рассуждений, проведенных в лекциях "3" и "8" . В разделе 15.7* приводится новый неожиданный результат, доказанный в 1997 году.

Проблема эквивалентности конечных автоматов (или, что то же самое, регулярных выражений) разрешима, но, к сожалению, она сложна, то есть нахождение ответа индивидуальной задачи требует (в некотором смысле) много времени. В разделе 15.9* указывается, что даже для регулярных выражений без итерации (которые, очевидно, соответствуют конечным автоматам без циклов) проблема неэквивалентности NP -полна (необходимые определения из теории сложности вычислений приведены в разделе 15.8*).

15.1. Неукорачивающие грамматики

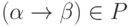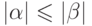Определение 15.1.1. Порождающая грамматика $\lalg N , \Sigma , P , S \ralg$ называется неукорачивающей (noncontracting), если для каждого правила $( \alpha \tto \beta ) \in P$ выполняется неравенство $| \alpha | \leq | \beta |$ .

Теорема 15.1.2. Существует алгоритм, позволяющий по произвольной неукорачивающей грамматике G и по слову w узнать, верно ли, что $w \in L(G)$ .

Теорема 15.1.3. Каждая контекстная грамматика является неукорачивающей. Каждая неукорачивающая грамматика эквивалентна некоторой контекстной грамматике.

Пример 15.1.4. Грамматика

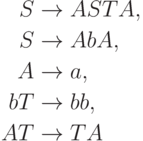
$\begin{align*} S \; & {\to} \; ASTA , \\ S \; & {\to} \; AbA , \\ A \; & {\to} \; a , \\ bT \; & {\to} \; bb , \\ AT \; & {\to} \; TA \end{align*}$

эквивалентна контекстной грамматике из примера 1.5.4.

Упражнение 15.1.5. Найти неукорачивающую грамматику, порождающую язык 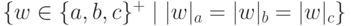$\{ w \in \{a,b,c\}^+ \mid | w |_a = | w |_b = | w |_c \}$ .

Упражнение 15.1.6. Найти неукорачивающую грамматику, порождающую язык 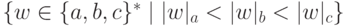$\{ w \in \{a,b,c\}^* \mid | w |_a < | w |_b < | w |_c \}$ .

Упражнение 15.1.7. Найти неукорачивающую грамматику, порождающую язык $\{ c^n d c^n d c^n \mid n \geq 0 \}$ .

Упражнение 15.1.7. Найти неукорачивающую грамматику, порождающую язык $\{ w c w \mid w \in \{a,b\}^* \}$ .

15.2*. Линейно ограниченные автоматы

Определение 15.2.1. Машина Тьюринга

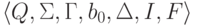
$\lalg Q , \Sigma , \Gamma , b_0 , \Delta , I , F \ralg$

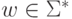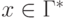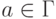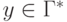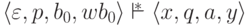называется линейно ограниченным автоматом (linear bounded automaton), если не существует таких $w \in \Sigma ^*$ , $x \in \Gamma ^*$ , $q \in Q$ , $a \in \Gamma$ и $y \in \Gamma ^*$ , что $\lp \varepsilon , p , b_0 , w b_0 \rp \overstar{\vdash} \lp x , q , a , y \rp$ и |xay| > |b₀wb₀|.

Теорема 15.2.2. Язык L, не содержащий пустого слова, порождается некоторой неукорачивающей грамматикой тогда и только тогда, когда существует линейно ограниченный автомат ( в общем случае недетерминированный ), допускающий язык L.

Замечание 15.2.3. Неизвестно, верен ли аналог теоремы 15.2.2 для детерминированных линейно ограниченных автоматов.

Теорема 15.2.4. Класс языков, порождаемых неукорачивающими грамматиками, то есть класс контекстных языков, замкнут относительно операций объединения, пересечения и дополнения.

Замкнутость относительно операции дополнения доказали в 1987 году (независимо друг от друга) Нил Иммерман (Neil Immerman) и Роберт Селепчени (Robert Szelepcs) (см. [Imm, Sze]). Замкнутость относительно операции объединения очевидна, а пересечение выражается через объединение и дополнение.

Упражнение 15.2.5. Является ли контекстным язык

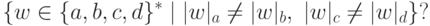
$\{ w \in \{a,b,c,d\}^* \mid | w |_a \neq | w |_b ,\ | w |_c \neq | w |_d \} ?$

Упражнение 15.2.6. Является ли контекстным язык

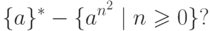
$\{a\}^* \sminus \{ a^{n^2} \mid n \geq 0 \} ?$

15.3. Проблема выводимости слова

Теорема 15.3.1. Существует алгоритм, позволяющий по произвольной контекстно-свободной грамматике G узнать, верно ли, что 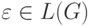$\varepsilon \in L(G)$ .

Теорема 15.3.2. Существует алгоритм, позволяющий по произвольной контекстно-свободной грамматике G и по слову w узнать, верно ли, что $w \in L(G)$ .

Упражнение 15.3.3. Принадлежит ли слово aaaaabbbabb языку, порождаемому грамматикой

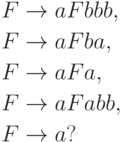
$\begin{align*} F \; & {\to} \; a F bbb , \\ F \; & {\to} \; a F ba , \\ F \; & {\to} \; a F a , \\ F \; & {\to} \; a F abb , \\ F \; & {\to} \; a ? \end{align*}$

Упражнение 15.3.4. Принадлежит ли слово abababa языку, порождаемому грамматикой

$\begin{align*} J \; & {\to} \; a a , \\ J \; & {\to} \; F b F , \\ F \; & {\to} \; a J , \\ F \; & {\to} \; J b , \\ F \; & {\to} \; b F a , \\ F \; & {\to} \; \varepsilon ? \end{align*}$

Дальше >>

Авторизоваться

Математическая теория формальных языков

Алгоритмически разрешимые проблемы

15.1. Неукорачивающие грамматики

15.2*. Линейно ограниченные автоматы

15.3. Проблема выводимости слова

Вопросы и ответы