Быстрое дифференцирование, двойственность и обратное распространение ошибки
Двойственное функционирование и быстрое дифференцирование
Вычисление градиента сложной функции многих переменных также будет представлено как некоторый вычислительный процесс, в ходе которого сигналы перемещаются в обратном направлении - от выходных элементов графа к входным. И так же, как при вычислении сложной функции, будет явно представлено прохождение каждого узла (подобно тому, как это сделано в уравнении функционирования (4)), а весь процесс в целом будет складываться из таких элементарных фрагментов за счет структуры связей между узлами. Сама эта структура - та же самая, что и для прямого процесса.
Всюду в этом разделе область интерпретации - действительная прямая, а все функции дифференцируемы.
Основной инструмент при построении двойственного функционирования - формула для дифференцирования "двухслойной" сложной функции нескольких переменных
 |
( 5) |
При проведении индукции по числу слоев нам придется использовать графы с несколькими выходными вершинами, описанные в предыдущем разделе, поэтому сразу будем рассматривать этот более общий случай.
Итак, пусть G - связный (но не обязательно ориентированно связный) ориентированный граф без ориентированных циклов. Как и выше, v(G) - множество вершин G, e(G) - множество ребер. Пусть, далее, каждой вершине  сопоставлена метка - символ алфавита
сопоставлена метка - символ алфавита 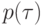 , а каждому ребру
, а каждому ребру  сопоставляется метка - конечное множество натуральных чисел
сопоставляется метка - конечное множество натуральных чисел 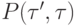 и выполнено условие согласования A: если для данного
и выполнено условие согласования A: если для данного  множество входящих ребер
множество входящих ребер 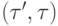 непусто, то
непусто, то 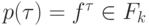 (является k -местным функциональным символом при некотором k ) и семейство множеств
(является k -местным функциональным символом при некотором k ) и семейство множеств
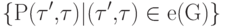
 образует разбиение множества номеров {1,...,k}. Для каждой вершины
образует разбиение множества номеров {1,...,k}. Для каждой вершины  обозначим множество входящих в нее ребер
обозначим множество входящих в нее ребер  , а выходящих из нее -
, а выходящих из нее -  .
.Пусть указана интерпретация всех символов, отмечающих вершины графа, значения переменных, отвечающих входным вершинам и уравнениям функционирования (4) определены значения  для всех вершин графа. В результате определены значения всех сложных функций, формулы для которых являются термами, соответствующими вершинам графа G. Процесс вычисления
для всех вершин графа. В результате определены значения всех сложных функций, формулы для которых являются термами, соответствующими вершинам графа G. Процесс вычисления  будем называть прямым в противовес обратному или двойственному, к описанию которого мы переходим.
будем называть прямым в противовес обратному или двойственному, к описанию которого мы переходим.
При заданных  для каждой вершины и каждого ребра строятся переменные двойственного функционирования (или, более кратко, двойственные переменные ). Будем обозначать их
для каждой вершины и каждого ребра строятся переменные двойственного функционирования (или, более кратко, двойственные переменные ). Будем обозначать их  для вершин и
для вершин и 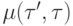 - для ребер.
- для ребер.
Для выходных вершин  являются независимыми переменными. Пусть их значения заданы. Для вершины
являются независимыми переменными. Пусть их значения заданы. Для вершины 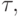 не являющейся выходной, значение
не являющейся выходной, значение  есть сумма значений двойственных переменных, соответствующих выходящим из
есть сумма значений двойственных переменных, соответствующих выходящим из  ребрам:
ребрам:
 |
( 6) |
Для ребра 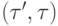 значение
значение 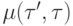 определяется согласно формуле (5):
определяется согласно формуле (5):
 |
( 7) |
В формуле (7)  - метка ребра
- метка ребра 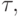
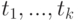 - аргументы "простой" функции
- аргументы "простой" функции  , а производные
, а производные  берутся при условиях, определяемых прямым процессом:
берутся при условиях, определяемых прямым процессом:
 |
( 8) |
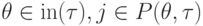 .
.Для каждого  такое
такое  существует и единственно в силу того, что метки входящих в вершину
существует и единственно в силу того, что метки входящих в вершину  ребер образуют разбиение множества номеров {1,...,k}.
ребер образуют разбиение множества номеров {1,...,k}.
В самом распространенном случае все метки ребер 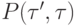 содержат по одному элементу. В этом случае формула (7) приобретает особенно простой вид
содержат по одному элементу. В этом случае формула (7) приобретает особенно простой вид

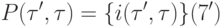
Используя (6)-(8), можно записать правила вычисления двойственных переменных для вершин, не использующие двойственных переменных для ребер:
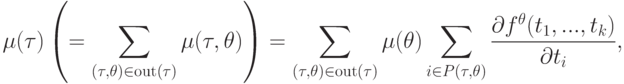 |
( 9) |
где производные  берутся при условиях
берутся при условиях
 |
( 10) |
 .
.Греческими буквами  ,
,  ,
,  здесь обозначены вершины графа.
здесь обозначены вершины графа.
Опять же, в распространенном случае, когда все 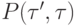 одноэлементны, применяем (7') вместо (7) и получаем
одноэлементны, применяем (7') вместо (7) и получаем
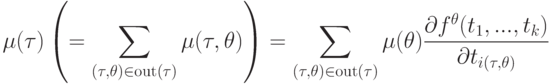
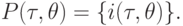 |
( 9') |
Напомним, что каждой вершине 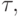 принадлежащей ненулевому слою графа G, соответствуют терм
принадлежащей ненулевому слою графа G, соответствуют терм  и сложная функция
и сложная функция 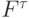 от независимых переменных и констант, отмечающих вершины нулевого слоя G.
от независимых переменных и констант, отмечающих вершины нулевого слоя G.
Процесс вычисления двойственных переменных организуется послойно от выходных вершин к входным и часто называется процессом обратного распространения (back propagation) или просто обратным процессом.
Теорема 5. Пусть задана интерпретация всех символов, отмечающих вершины графа G, определены значения независимых переменных (а также констант), соответствующих вершинам входного слоя 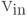 и значения независимых переменных двойственного функционирования
и значения независимых переменных двойственного функционирования  для вершин выходного слоя
для вершин выходного слоя 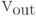 . Тогда для любого
. Тогда для любого 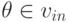
 |
( 11) |
где 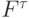 - соответствующая вершине
- соответствующая вершине  функция от независимых переменных и констант, отмечающих вершины нулевого слоя G,
функция от независимых переменных и констант, отмечающих вершины нулевого слоя G, 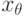 - соответствующая вершине
- соответствующая вершине 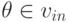 переменная или константа, а производные в (11) берутся при фиксированных значениях прочих переменных и констант.
переменная или константа, а производные в (11) берутся при фиксированных значениях прочих переменных и констант.
Доказательство проводится индукцией по числу слоев. Для графов из двух слоев - нулевого и первого - теорема очевидна. Спуск от i+1 -слойных графов к i -слойным производится с помощью формулы 5.
Прохождение вершины графа и прилегающих к ней ребер при прямом и обратном процессах проиллюстрировано на рис. 3.3.

