Быстрое дифференцирование, двойственность и обратное распространение ошибки
Вычисления на ориентированном графе
Для дальнейшего полезно обобщение изложенных конструкций, предназначенное для описания одновременного вычисления нескольких сложных функций.
Пусть G - связный (но не обязательно ориентированно связный) ориентированный граф без ориентированных циклов. Как и выше, множество вершин G обозначаем v(G), множество ребер - e(G). Пусть, далее, каждой вершине  сопоставлена метка - символ алфавита
сопоставлена метка - символ алфавита 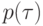 , а каждому ребру
, а каждому ребру  сопоставляется метка - конечное множество натуральных чисел
сопоставляется метка - конечное множество натуральных чисел 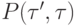 и выполнено условие согласования A: если для данного
и выполнено условие согласования A: если для данного  множество входящих ребер
множество входящих ребер 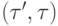 непусто, то
непусто, то 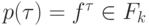 (является k -местным функциональным символом при некотором k ) и семейство множеств
(является k -местным функциональным символом при некотором k ) и семейство множеств
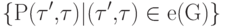
 образует разбиение множества номеров {1,...,k}.
образует разбиение множества номеров {1,...,k}.С помощью транзитивного замыкания G устанавливаем на множестве его вершин v(G) отношения частичного порядка: 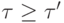 , если существует ориентированный путь, ведущий от
, если существует ориентированный путь, ведущий от 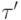 к
к 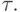 Из-за отсутствия ориентированных циклов это отношение антисимметрично: если
Из-за отсутствия ориентированных циклов это отношение антисимметрично: если 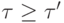 и
и 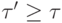 , то
, то  совпадает с
совпадает с 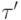 . Минимальные вершины (к которым не ведет ни одного ребра) называем входными, а максимальные (от которых не идет ни одного ребра) - выходными. Обозначим множество входных вершин
. Минимальные вершины (к которым не ведет ни одного ребра) называем входными, а максимальные (от которых не идет ни одного ребра) - выходными. Обозначим множество входных вершин 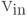 , а выходных -
, а выходных - 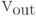 . Метки входных вершин являются символами переменных или констант, метки остальных вершин - функциональные символы.
. Метки входных вершин являются символами переменных или констант, метки остальных вершин - функциональные символы.
Определим послойную структуру:  . Нулевой слой состоит из минимальных вершин, первый слой из минимальных вершин графа, получаемого удалением из G нулевого слоя и выходящих из него ребер и т.д. - i+1 -й слой состоит из минимальных вершин графа, получаемого удалением из G всех вершин объединения
. Нулевой слой состоит из минимальных вершин, первый слой из минимальных вершин графа, получаемого удалением из G нулевого слоя и выходящих из него ребер и т.д. - i+1 -й слой состоит из минимальных вершин графа, получаемого удалением из G всех вершин объединения  и содержащих их ребер. Последний слой состоит только из выходных вершин. Предыдущие слои также могут содержать выходные вершины.
и содержащих их ребер. Последний слой состоит только из выходных вершин. Предыдущие слои также могут содержать выходные вершины.
С каждой вершиной графа  однозначно связан терм (который мы, следуя традиции предыдущего раздела, также будем обозначать
однозначно связан терм (который мы, следуя традиции предыдущего раздела, также будем обозначать  ). Для его построения удалим из G все вершины, кроме тех, от которых к
). Для его построения удалим из G все вершины, кроме тех, от которых к  можно пройти по ориентированному пути, а также связанные с ними ребра. Полученный граф обозначим
можно пройти по ориентированному пути, а также связанные с ними ребра. Полученный граф обозначим 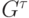 :
:

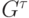 удовлетворяет условиям теоремы 3, поэтому по нему единственным образом восстанавливается терм (и соответствующая сложная функция).
удовлетворяет условиям теоремы 3, поэтому по нему единственным образом восстанавливается терм (и соответствующая сложная функция).Пусть задано множество D - область интерпретации и указана интерпретация всех символов, отмечающих вершины графа, а также значения переменных, отвечающих входным вершинам. Тогда по уравнениям функционирования (4) (они полностью сохраняются и для рассматриваемых графов) можно определить значения  для всех вершин графа. В результате определяются значения всех сложных функций, формулы для которых являются термами, соответствующими вершинам графа G.
для всех вершин графа. В результате определяются значения всех сложных функций, формулы для которых являются термами, соответствующими вершинам графа G.
Описанные общие графы могут появляться в различных ситуациях. Для дальнейшего важно то, что такие графы возникают, если из графа вычисления сложной функции удалить один или несколько последних слоев.
Двойственное функционирование, дифференциальные операторы и градиент сложной функции
Производная сложной функции одного переменного
Основную идею двойственного функционирования можно понять уже на простейшем примере. Рассмотрим вычисление производной сложной функции одного переменного. Пусть заданы функции одного переменного f1(A),f2(A),...,fn(A). Образуем из них сложную функцию
F(x)=fn(fn-1 (...(f1 (x))...)). (1)
Можно представить вычисление F(x) как результат работы n автоматов, каждый из которых имеет один вход и выдает на выходе значение fi(A), где A - входной сигнал ( рис. 3.2, а). Чтобы построить систему автоматов, вычисляющую F'(x), надо дополнить исходные автоматы такими, которые вычисляют функции fi'(A), где A - входной сигнал (важно различать производную fi по входному сигналу, то есть по аргументу функции fi, и производную сложной функции fi(A(x)) по x ; fi'(A) - производные по A ).
Для вычисления F'(x) потребуется еще цепочка из n-1 одинаковых автоматов, имеющих по два входа, по одному выходу и подающих на выход произведение входов. Тогда формулу производной сложной функции
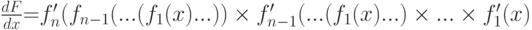
можно реализовать с помощью сети автоматов, изображенной на рис. 3.2, б. Сначала по этой схеме вычисления идут слева направо: на входы f1 и f1' подаются значения x, после вычислений f1(x) это число подается на входы f2 и f2' и т.д. В конце цепочки оказываются вычисленными все fi (fi-1 (...)) и fi'(fi-1 (...)).

Рис. 3.2. Схематическое представление вычисления сложной функции одного переменного и ее производных.
Тем самым, для каждого автомата нижней строки, кроме самого правого, оказывается сформированным по одному значению входа, а у самого правого - оба, поэтому он может сработать и начать передачу сигнала в обратном направлении - справа налево. Это обратное движение есть последовательное вычисление попарных произведений и передача их налево. В конце получаем 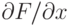 .
.
