Возможности нейронных сетей
А теперь - теорема Колмогорова, завершившая серию исследований для непрерывных функций:
Каждая непрерывная функция n переменных, заданная на единичном кубе n -мерного пространства, представима в виде
![f(x_1 ,x_2 ,...,x_n )=\sum\limits_{q=1}^{2n+1}{h_q}\left[{\sum\limits_{p=1}^n {\varphi_q^p (x_p)} }\right]](/sites/default/files/tex_cache/977d81ead15487e8274448cacc939bf4.png) |
( 1) |
где функции 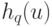 непрерывны, а функции
непрерывны, а функции  , кроме того, еще и стандартны, т.е. не зависят от выбора функции f.
, кроме того, еще и стандартны, т.е. не зависят от выбора функции f.
В частности, каждая непрерывная функция двух переменных x, y представима в виде
![f(x,y)=\sum\limits_{q=1}^5 {h_q \left[{\varphi_q (x)+\psi_q (y)}\right]}
,](/sites/default/files/tex_cache/cb99f5372bb9ef34abc700a7aba017d4.png) |
( 2) |
Доказательство настолько просто, изящно и поучительно, что мы приведем его практически полностью для случая n=2, следуя изложению В.И.Арнольда [1.5]. Возможность представления (2) доказывается в несколько этапов.
1. "Внутренние" функции  и
и  представления (2) совершенно не зависят от разлагаемой функции
представления (2) совершенно не зависят от разлагаемой функции 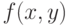 .
.
Для определения этих функций нам понадобятся некоторые предварительные построения. Рассмотрим изображенный на рис. 1.8 "город" - систему одинаковых "кварталов" (непересекающихся замкнутых квадратов), разделенных узкими "улицами" одной и той же ширины. Уменьшим гомотетично наш "город" в 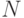 раз; за центр гомотетии можно принять, например, точку
раз; за центр гомотетии можно принять, например, точку 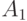 - мы получим новый" город", который будем называть "городом ранга 2". "Город ранга 3" точно также получается из "города ранга 2" гомотетичным уменьшением с коэффициентом гомотетии
- мы получим новый" город", который будем называть "городом ранга 2". "Город ранга 3" точно также получается из "города ранга 2" гомотетичным уменьшением с коэффициентом гомотетии  ; "город ранга 4" получается гомотетичным уменьшением в
; "город ранга 4" получается гомотетичным уменьшением в 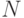 раз "города ранга 3" и т.д. Вообще "город ранга
раз "города ранга 3" и т.д. Вообще "город ранга  " получается из исходного "города" (который мы будем называть "городом первого ранга") гомотетичным уменьшением в
" получается из исходного "города" (который мы будем называть "городом первого ранга") гомотетичным уменьшением в  раз (с центром гомотетии в
раз (с центром гомотетии в 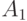 ; впрочем, выбор центра гомотетии не существенен для дальнейшего).
; впрочем, выбор центра гомотетии не существенен для дальнейшего).
Построенную систему "городов" мы назовем 1 -й системой. "Город первого ранга  -й системы" (
-й системы" ( 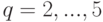 ) получается из изображенного на рис. 1.8 "города" при помощи параллельного переноса, совмещающего точку
) получается из изображенного на рис. 1.8 "города" при помощи параллельного переноса, совмещающего точку 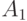 с точкой
с точкой  . Нетрудно понять, что "улицы" "города" можно выбрать настолько узкими, что каждая точка плоскости будет покрыта по крайней мере тремя кварталами наших пяти "городов первого ранга". Точно так же "город
. Нетрудно понять, что "улицы" "города" можно выбрать настолько узкими, что каждая точка плоскости будет покрыта по крайней мере тремя кварталами наших пяти "городов первого ранга". Точно так же "город  -го ранга"
-го ранга"  -й системы (
-й системы ( 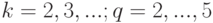 ) получается из "города
) получается из "города  -го ранга 1 -й системы" параллельным переносом, переводящим точку
-го ранга 1 -й системы" параллельным переносом, переводящим точку 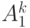 в точку
в точку  , где
, где 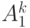 и
и  получаются из точек
получаются из точек 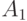 и
и  гомотетией, переводящей "город первого ранга" 1 -й системы (т.е. наш исходный "город") в "город
гомотетией, переводящей "город первого ранга" 1 -й системы (т.е. наш исходный "город") в "город  -го ранга"
той же системы; при этом каждая точка плоскости будет принадлежать кварталам по крайней мере трех из пяти "городов" любого фиксированного ранга
-го ранга"
той же системы; при этом каждая точка плоскости будет принадлежать кварталам по крайней мере трех из пяти "городов" любого фиксированного ранга  .
.
Функцию
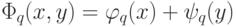
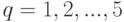 )
)мы определим теперь так, чтобы она разделяла любые два "квартала" каждого "города" системы  , т.е. чтобы множество значений, принимаемых
, т.е. чтобы множество значений, принимаемых 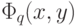 на определенном "квартале" "города
на определенном "квартале" "города  -го ранга" (здесь
-го ранга" (здесь  - произвольное фиксированное число)
- произвольное фиксированное число)  -й системы, не пересекалось с множеством значений, принимаемых
-й системы, не пересекалось с множеством значений, принимаемых 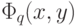 на любом другом "квартале" того же "города". При этом нам, разумеется, будет достаточно рассматривать функцию
на любом другом "квартале" того же "города". При этом нам, разумеется, будет достаточно рассматривать функцию 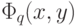 на единичном квадрате (а не на всей плоскости).
на единичном квадрате (а не на всей плоскости).
Для того, чтобы функция 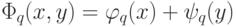 разделяла "кварталы" "города первого ранга", можно потребовать, например, чтобы
разделяла "кварталы" "города первого ранга", можно потребовать, например, чтобы  на проекциях "кварталов" "города" на ось
на проекциях "кварталов" "города" на ось  весьма мало отличалась от различных целых чисел, а
весьма мало отличалась от различных целых чисел, а  на проекциях "кварталов" на ось
на проекциях "кварталов" на ось  весьма мало отличалась от различных кратных
весьма мало отличалась от различных кратных 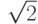 (ибо
(ибо  при целых
при целых  ,
,  ,
,  ,
,  , лишь если
, лишь если 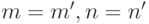 ). При этом наложенные условия не определяют пока еще, разумеется, функций
). При этом наложенные условия не определяют пока еще, разумеется, функций  и
и  (на "улицах" функция
(на "улицах" функция 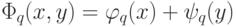 вообще пока может задаваться совершенно произвольно); используя это,
можно подобрать границы значений
вообще пока может задаваться совершенно произвольно); используя это,
можно подобрать границы значений  и
и  на "кварталах" "города второго ранга" так, чтобы функция
на "кварталах" "города второго ранга" так, чтобы функция 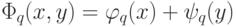 разделяла не только "кварталы" "города 1 -го ранга", но и "кварталы" "города 2 -го ранга". Намеченную программу можно осуществить, если
разделяла не только "кварталы" "города 1 -го ранга", но и "кварталы" "города 2 -го ранга". Намеченную программу можно осуществить, если 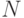 достаточно велико (так что кварталы последующих рангов не соединяют кварталы предыдущих). А.Н. Колмогоров выбрал
достаточно велико (так что кварталы последующих рангов не соединяют кварталы предыдущих). А.Н. Колмогоров выбрал  . Привлекая подобным же образом к рассмотрению "города" последующих рангов и уточняя каждый раз значения функций
. Привлекая подобным же образом к рассмотрению "города" последующих рангов и уточняя каждый раз значения функций  и
и  , мы в пределе получим непрерывные функции
, мы в пределе получим непрерывные функции  и
и  (можно даже потребовать, чтобы они были монотонными), удовлетворяющие поставленным условиям.
(можно даже потребовать, чтобы они были монотонными), удовлетворяющие поставленным условиям.
2. Функции 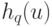 разложения (2), напротив того, существенно зависят от исходной функции
разложения (2), напротив того, существенно зависят от исходной функции 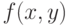 .
.
Для построения этих функций докажем прежде всего, что любую непрерывную функцию 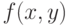 двух переменных
двух переменных  и
и  , заданную на единичном квадрате, можно представить в виде
, заданную на единичном квадрате, можно представить в виде
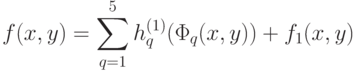 |
( 3) |
где 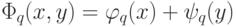 - функции, построенные выше, и
- функции, построенные выше, и
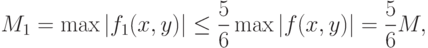 |
( 3^а) |
 |
( 3^б) |
 .
.Выберем ранг  столь большим, чтобы колебание (т.е. разность наибольшего и наименьшего значений) функции
столь большим, чтобы колебание (т.е. разность наибольшего и наименьшего значений) функции 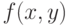 на каждом "квартале" любого из "городов ранга
на каждом "квартале" любого из "городов ранга  " не превосходило
" не превосходило 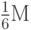 ; это, разумеется, возможно, так как с ростом ранга
; это, разумеется, возможно, так как с ростом ранга  размеры " кварталов" уменьшаются неограниченно. Далее, пусть
размеры " кварталов" уменьшаются неограниченно. Далее, пусть  - определенный "квартал" "города 1 -й системы" (и выбранного ранга
- определенный "квартал" "города 1 -й системы" (и выбранного ранга  ); в таком случае (непрерывная) функция
); в таком случае (непрерывная) функция 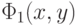 принимает на этом "квартале" значения, принадлежащие определенному сегменту
принимает на этом "квартале" значения, принадлежащие определенному сегменту 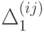 числовой оси (причем в силу определения функции
числовой оси (причем в силу определения функции 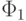 этот сегмент не пересекается с сегментами значений, принимаемых
этот сегмент не пересекается с сегментами значений, принимаемых 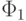 на всех других "кварталах"). Положим теперь функцию
на всех других "кварталах"). Положим теперь функцию 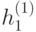 на сегменте
на сегменте 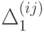 постоянной, равной
постоянной, равной  значения, принимаемого функцией
значения, принимаемого функцией 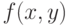 в какой-либо (безразлично какой) внутренней точке
в какой-либо (безразлично какой) внутренней точке  квартала
квартала  (эту точку можно назвать "центром квартала"). Таким же образом мы определим функцию
(эту точку можно назвать "центром квартала"). Таким же образом мы определим функцию 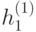 на любом другом из сегментов, задаваемых значениями функции
на любом другом из сегментов, задаваемых значениями функции 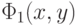 на "кварталах" "города
на "кварталах" "города  -го ранга" 1 -й системы; при этом все значения
-го ранга" 1 -й системы; при этом все значения 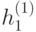 будут по модулю не превосходить
будут по модулю не превосходить 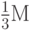 (ибо значение
(ибо значение 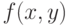 в "центре" любого "квартала" по модулю не превосходит
в "центре" любого "квартала" по модулю не превосходит  ). Доопределим теперь функцию
). Доопределим теперь функцию 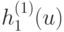 при тех значениях аргумента
при тех значениях аргумента  , при каких она еще не определена, произвольно, с тем лишь, чтобы она была непрерывна и чтобы выполнялось неравенство (3б); совершенно аналогично определим и все остальные функции
, при каких она еще не определена, произвольно, с тем лишь, чтобы она была непрерывна и чтобы выполнялось неравенство (3б); совершенно аналогично определим и все остальные функции  (
( 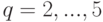 ).
).
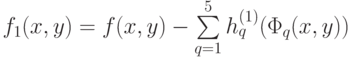
удовлетворяет условию (3а), т.е. что 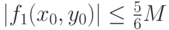 , где
, где 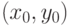 - произвольная точка единичного квадрата. Эта точка (как и все точки плоскости) принадлежит по крайней мере трем кварталам "городов ранга
- произвольная точка единичного квадрата. Эта точка (как и все точки плоскости) принадлежит по крайней мере трем кварталам "городов ранга  "; поэтому заведомо найдутся такие три из пяти функций
"; поэтому заведомо найдутся такие три из пяти функций 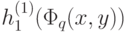 , которые принимают в точке
, которые принимают в точке 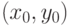 значение, равное
значение, равное  значения
значения 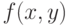 в "центре" соответствующего "квартала", т.е. отличающееся от
в "центре" соответствующего "квартала", т.е. отличающееся от 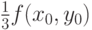 не более чем на
не более чем на 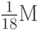 (ибо колебание
(ибо колебание 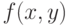 на каждом квартале не превосходит
на каждом квартале не превосходит 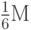 ); сумма этих трех значений
); сумма этих трех значений  будет отличаться от
будет отличаться от  по модулю не более чем на
по модулю не более чем на 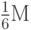 . А так как каждое из оставшихся двух чисел
. А так как каждое из оставшихся двух чисел  в силу (3) по модулю не превосходит
в силу (3) по модулю не превосходит 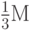 то мы получаем:
то мы получаем:

что и доказывает (3а).

