Возможности нейронных сетей
Применим теперь то же разложение (3) к входящей в (3) функции 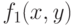 ; мы получим:
; мы получим:
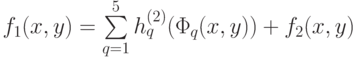
или
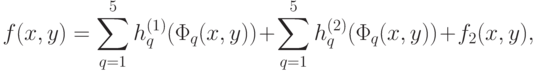
где
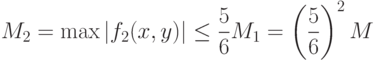
и
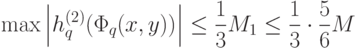
 ).
).Затем мы применим разложение (3) к полученной функции 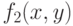 и т.д.; после
и т.д.; после  -кратного применения этого разложения мы будем иметь:
-кратного применения этого разложения мы будем иметь:
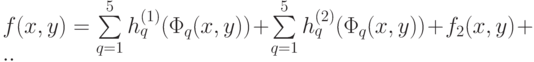 .
.
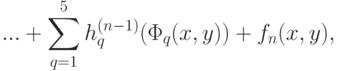
где
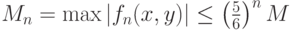
и
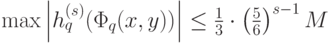 (
( 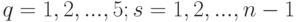 ).
).
Последние оценки показывают, что при 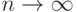 получим:
получим:
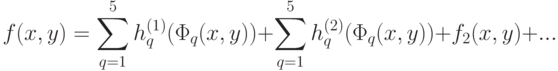
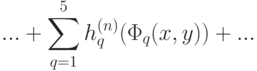
где стоящий справа бесконечный ряд сходится равномерно; также и каждый из пяти рядов
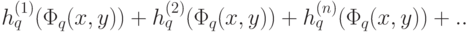 .
(
.
( 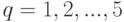 )
)
сходится равномерно, что позволяет ввести обозначения
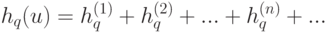
 ).
).Итак, окончательно получаем:
![f(x,y)=\sum\limits_{q=1}^5 {h_q (\Phi_q (x,y))} =\sum\limits_{q=1}^5 h_q \left[{\varphi_q (x)+\psi_q (y)} \right]
,](/sites/default/files/tex_cache/8e60dc85c7810f18dd352d605c6d1a62.png)
то есть требуемое разложение (2).
До сих пор речь шла о точном представлении функций многих переменных с помощью функций одного переменного. Оказалось, что в классе непрерывных функций такое представление возможно. Но кроме вопроса о точном представлении существует еще один - об аппроксимации. Можно даже предположить, что он важнее - вычисление большинства функций производится приближенно даже при наличии "точных" формул.
Приближение функций многочленами и рациональными функциями имеет историю, еще более давнюю, чем проблема точного представления. Знаменитая теорема Вейерштрасса утверждает, что непрерывную функцию нескольких переменных 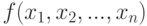 на замкнутом ограниченном множестве Q можно равномерно приблизить последовательностью полиномов: для любого
на замкнутом ограниченном множестве Q можно равномерно приблизить последовательностью полиномов: для любого 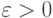 существует такой многочлен
существует такой многочлен 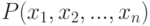 , что
, что
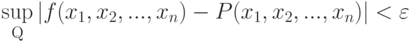
Чтобы сформулировать обобщения и усиления теоремы Вейерштрасса, необходимо перейти к несколько более абстрактному языку. Рассмотрим компактное пространство X и алгебру C(X) непрерывных функций на X с вещественными значениями.
Сильным обобщением теоремы о возможности равномерного приближения непрерывных функций многочленами является теорема Стоуна [1.6, 1.7]:
Пусть 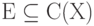 - замкнутая подалгебра в C(X),
- замкнутая подалгебра в C(X),  и функции из E разделяют точки в X (то есть для любых различных
и функции из E разделяют точки в X (то есть для любых различных  существует такая функция
существует такая функция 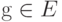 , что
, что  ). Тогда E=C(X) .
). Тогда E=C(X) .
Теорема Стоуна обобщает теорему Вейерштрасса по двум направлениям. Во-первых, рассматриваются функции на произвольном компакте, а не только функции многих действительных переменных. Во-вторых, доказано утверждение, новое даже для функций одного переменного (не говоря уже о многих): плотно не только множество многочленов от координатных функций, но вообще кольцо многочленов от любого набора функций, разделяющих точки. Следовательно, плотно множество тригонометрических многочленов, множество линейных комбинаций функций вида exp[-(x-x0,Q(x-x0))], где (x,Qx) - положительно определенная квадратичная форма и др.
Дан рецепт конструирования таких обобщений: достаточно взять произвольный набор функций, разделяющих точки, построить кольцо многочленов от них - и получим плотное в C(X) множество функций.
Разложения по ортогональным системам функций (ряды Фурье и их многочисленные обобщения) не дают, вообще говоря, равномерного приближения разлагаемых функций - как правило, можно гарантировать лишь монотонное стремление к нулю интеграла квадрата остатка "функция минус приближение" с какой-либо положительной весовой функцией. Все же, обращаясь к задаче аппроксимации, нельзя забывать об ортогональных разложениях. Для ряда прикладных задач простота получения коэффициентов такого разложения может оказаться важнее, чем отсутствие гарантированной равномерности приближения.
Так существуют ли функции многих переменных? В каком-то смысле - да, в каком-то - нет. Все непрерывные функции многих переменных могут быть получены из непрерывных функций одного переменного с помощью линейных операций и суперпозиции. Требования гладкости и аналитичности существенно усложняют вопрос. На этом фоне совершенно неожиданно выглядит тот факт, что любой многочлен от многих переменных может быть получен из одного произвольного нелинейного многочлена от одного переменного с помощью линейных операций и суперпозиции. Простое доказательство этой теоремы будет дано в разделе 6.
