|
Здравствуйте,при покупке печатной формы сертификата,будут ли выданы обе печатные сторны? |
Лекция 7: Формальные спецификации, доказательство и верификация программ
6.2.2. Доказательство конкретности с помощью утверждений
Рассмотрим формальное доказательство программы, заданной структурной логической схемой и совокупностью утверждений, задаваемых логическими операторами, комбинациями переменных (true/false), операциями (конъюнкция, дизъюнкция и др.) и кванторами всеобщности и существования (табл. 6.1).
| Логические операции | ||
|---|---|---|
| Название | Примеры | Значение |
| Конъюнкция | 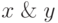 |
 и и 
|
| Дизъюнкция |  |
 или или 
|
| Отрицание | 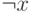 |
не 
|
| Импликация |  |
если  то то 
|
| Эквивалентность |  |
 равнозначно равнозначно 
|
| Квантор всеобщности | 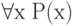 |
для всех  , условие истинно , условие истинно |
| Квантор существования | 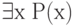 |
существует  ,
для которого ,
для которого 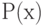 истина истина |
Цель алгоритма программы - построение для массива целых чисел  длины
длины ![N (array Т[1:N])](/sites/default/files/tex_cache/bd858aa7fcd5adbe67e0ff0534514c4e.png) эквивалентного массива
эквивалентного массива  той же длины
той же длины  , что и массив
, что и массив  .
Элементы в массиве
.
Элементы в массиве  должны располагаться в порядке возрастания их значений.
Данный алгоритм реализуется сортировкой элементов исходного массива
должны располагаться в порядке возрастания их значений.
Данный алгоритм реализуется сортировкой элементов исходного массива  по их возрастанию.
Доказательство правильности алгоритма сортировки элементов массива
по их возрастанию.
Доказательство правильности алгоритма сортировки элементов массива  проводится с использованием ряда утверждений относительно элементов этого алгоритма,
которые описываются пунктами П1- П6.
проводится с использованием ряда утверждений относительно элементов этого алгоритма,
которые описываются пунктами П1- П6.
- Входное условие алгоритма задается в виде начального утверждения:
![А_{beg}: (Т [1:N]\text{ - массив целых}) \;\& \; (Т^\prime[1:N ]\text{ - массив целых })](/sites/default/files/tex_cache/40fa15f2295dfc83802264368cfbf55a.png)
Выходное утверждение
 - это конъюнкция таких условий:
- это конъюнкция таких условий:-
 ,
, -
 ,
, -
 ,
,
т.е.
![А_{beg} \text{ - это }(Т [1:N]\text{ - массив целых}) \;\& \; (Т^\prime[1:N ]\text{ - массив целых }) \\
\& \; \forall{i}\text{, если }i \le N\text{, то }\exists{j}(T^\prime(i) \le T^\prime(j)),\\
\& \; \forall{i}\text{, если }i \le N\text{, то }(T^\prime(i) \le T^\prime(i+1)).](/sites/default/files/tex_cache/ad9dc96de05174bdaf243c2fa9ae5e23.png)
Расположение элементов массива
 в порядке возрастания их величин в массиве
в порядке возрастания их величин в массиве  осуществляется алгоритмом пузырьковой сортировки, суть которого заключается в предварительном копировании массив
осуществляется алгоритмом пузырьковой сортировки, суть которого заключается в предварительном копировании массив  в массив
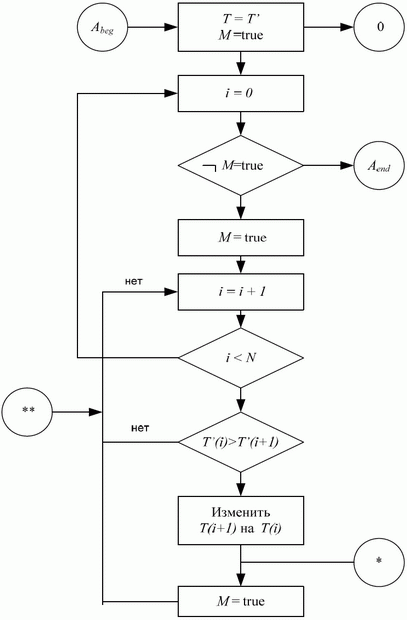
в массив  , а затем проводится сортировка элементов согласно условия их возрастания. Алгоритм сортировки представлен на блоксхеме (рис. 6.2).
, а затем проводится сортировка элементов согласно условия их возрастания. Алгоритм сортировки представлен на блоксхеме (рис. 6.2).Операторы алгоритма размещены в прямоугольниках, условия выбора альтернативных путей - параллелограммами, точки с начальным
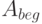 и конечным
и конечным  условиями и состояниями алгоритма - кружками.
В кружках также заданы: начальное состояние -
условиями и состояниями алгоритма - кружками.
В кружках также заданы: начальное состояние -  ,
состояние после обмена местами двух соседних элементов в массиве
,
состояние после обмена местами двух соседних элементов в массиве  -
одна звездочка, состояние после обмена местами всех пар за один проход всего массива
-
одна звездочка, состояние после обмена местами всех пар за один проход всего массива  - две звездочки.
- две звездочки.Кроме уже известных переменных
 ,
,  и
и  ,
в алгоритме использованы еще две переменные:
,
в алгоритме использованы еще две переменные:  - целое и
- целое и  - булева переменная,
значением которой являются логические константы
- булева переменная,
значением которой являются логические константы 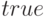 и
и 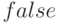 .
. -
- Для доказательства того, что алгоритм действительно обеспечивает выполнение исходных условий, рассмотрим динамику их выполнения последовательно в определенных точках алгоритма.
Заметим, что точки делят алгоритм на соответствующие части, правильность любой из них обосновывается в отдельности.
Так, оператор присваивания означает, что для всех
 (
( 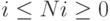 )
выполняется (
)
выполняется ( ![T^\prime[i] : = T[i]](/sites/default/files/tex_cache/0490e0ef725f37659bf8a73f5837070c.png) ).
Результат выполнения алгоритма в точке с нулем может быть выражен утверждением
).
Результат выполнения алгоритма в точке с нулем может быть выражен утверждением![(T[1: N]\text{ - массив целых}) \;\&\; (T^\prime[1: N]\text{ - массив целых})\\
\&\; (\forall{i}\text{, если }i \le N (T[i] = T[i])).](/sites/default/files/tex_cache/b919fc55d4d446e255a255d514ad5231.png)
Доказательство очевидно, поскольку за семантикой оператора присваивания (поэлементная пересылка чисел из
 в
в  )
сами элементы при этом не изменяются, к тому же в данной точке их порядокв
)
сами элементы при этом не изменяются, к тому же в данной точке их порядокв  и
и  одинаковый.
Итак, получили, что выполняется условие б) исходного утверждения.
одинаковый.
Итак, получили, что выполняется условие б) исходного утверждения.Заметим, что первая строка доказанного утверждения совпадает с условием а) исходного утверждения
 и остается справедливой до конца работы алгоритма,
поэтому в следующих утверждениях приводиться не будет.
и остается справедливой до конца работы алгоритма,
поэтому в следующих утверждениях приводиться не будет.В точке с одной звездочкой выполнен оператор
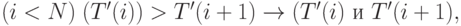 который меняет местами элементы.
который меняет местами элементы.В результате работы оператора будет справедливым такое утверждение:

которое является частью условия в) утверждения
 (для одной конкретной пары смежных элементов массива
(для одной конкретной пары смежных элементов массива  ).
Очевидно также, что семантика оператора обмена местами не нарушает условие б) выходного утверждения
).
Очевидно также, что семантика оператора обмена местами не нарушает условие б) выходного утверждения  .
.В точке с двумя звездочками выполнены все возможные обмены местами пар смежных элементов массива
 за один проход через
за один проход через  , т.е. оператор обмена работал один или больше раз.
Однако пузырьковая сортировка не дает гарантии, что достигнуто упорядочение за один проход по массиву
, т.е. оператор обмена работал один или больше раз.
Однако пузырьковая сортировка не дает гарантии, что достигнуто упорядочение за один проход по массиву  ,
поскольку после очередного обмена индекс
,
поскольку после очередного обмена индекс  увеличивается на единицу независимо от того, как соотносится новый элемент
увеличивается на единицу независимо от того, как соотносится новый элемент  с элементом
с элементом  .
.В этой точке также справедливо утверждение
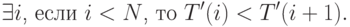
Часть алгоритма, обозначенная точкой с двумя звездочками, выполняется до тех пор, пока не будет упорядочен весь массив, т.е. не будет выполняться условие в) утверждения
 для всех элементов массива
для всех элементов массива  .
.Итак, выполнение исходных условий обеспечено порядком и соответствующей cемантикой операторов преобразования массива.
Доказано, что выполнение алгоритма программы завершено успешно, что означает ее правильность.
- Этот алгоритм можно представить в виде серии теорем, которые доказываются.
Начиная с первого утверждения и переходя от одного преобразования к другому, определяется индуктивный путь вывода.
Если одно утверждение - истинно, то истинно и другое.
Иными словами, если дано первое утверждение
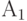 и первая точка преобразования
и первая точка преобразования  ,
то первая теорема -
,
то первая теорема - 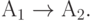
Если
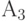 - следующая точка преобразования,
то второй теоремой будет
- следующая точка преобразования,
то второй теоремой будет  .
.Таким образом, формулируется общая теорема
 ,
где
,
где 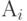 и
и 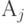 - смежные точки преобразования.
Эта теорема формулируетсятак, что если условие "истинное" в последней точке,
то истинно и выходное утверждение
- смежные точки преобразования.
Эта теорема формулируетсятак, что если условие "истинное" в последней точке,
то истинно и выходное утверждение 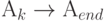 .
.Следовательно, можно возвратиться к точке преобразования
 и к предшествующей точке преобразования.
Доказав, что
и к предшествующей точке преобразования.
Доказав, что 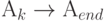 верно,
значит, верно и
верно,
значит, верно и 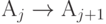 и так далее,
пока не получим, что
и так далее,
пока не получим, что  .
. - Далее специфицируются утверждения типа
 -
-  .
. - Чтобы доказать, что программа корректная,
необходимо последовательно расположить все утверждения, начиная с
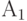 и заканчивая
и заканчивая  ,
этим подтверждает истинность входного и выходного условий.
,
этим подтверждает истинность входного и выходного условий. - Доказательство алгоритма программы завершено.