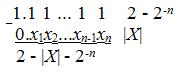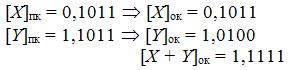Лекция 7: Способы представления чисел в ЭВМ. Сложение чисел в обратном и дополнительном кодах
Кодирование чисел в ЭВМ
Прямой код
Возможны два варианта изображения знаков чисел двоичными цифрами:
"+" обозначать "0", а "-" обозначать "1";
"+" обозначать "1", а "-" обозначать "0".
Оба варианта равноценны.
На практике в основном используется первый вариант.
При таком решении все положительные числа с фиксированной запятой имеют вид: 0, x-1x-2... x-n, а отрицательные: 1, x-1x-2... x-n (естественно, что запятая, между знаковым разрядом и самим числом внутри ЭВМ не кодируется). Код знака помещается слева от запятой на место разряда с весом 2°. Поэтому, если знак и цифровую часть числа рассматривать как единое целое, то изображение положительных чисел не изменяется и определяется интервалом 0 ≤ Х < 1, а все отрицательные числа изображаются положительными числами [Х], расположенными в интервале 1 ≤ [Х] <2 (так называемое, представление числа в прямом коде).
Рассмотренную связь между числом Х и его изображением в прямом коде - [Х]пк можно представить в следующем виде:
 |
( 7.1) |
Пример 7.1.
0.1012пк = +(1/2 +1/8) = +5/8
1.1012пк = -5/8
Число с фиксированной точкой в прямом коде имеет такое же представление, как и указанное в (7.1). Однако, здесь следует помнить, что двоичное число с фиксированной точкой имеет формат согласно (6.2). В этом случае числу 0.1012пк соответствует десятичное число +510, а числу 1.1012пк - -510.
Очевидно, что если рассматривать числа с фиксированной точкой или запятой в прямом коде вместе со знаком, то такая операция даже простейшем случае алгебраического сложения не может быть выполнена. Так для чисел с фиксированной точкой
01012пк = +510
10102пк = -210
При сложении этих чисел получим
что, конечно, является неправильным результатом.
Методика выполнения алгебраического сложения, рациональная для применения в ЭВМ, должна удовлетворять следующим условиям:
- обработка знаковых и цифровых разрядов суммируемых чисел X и Y должна производиться по одинаковым правилам с получением при этом правильного знака суммы;
- должна исключаться операция прямого вычитания, и вместо неё алгебраическое суммирование чисел разных знаков должно выполняться как сложение специальных кодов суммируемых чисел;
- должно определяться переполнение, соответствующее
 при условии, что абсолютное значение X и Y меньше единицы (здесь речь идет, естественно, о числах с фиксированной запятой).
при условии, что абсолютное значение X и Y меньше единицы (здесь речь идет, естественно, о числах с фиксированной запятой).
Всем указанным условиям удовлетворяет методика алгебраического сложения дополнительных и обратных кодов исходных чисел.
Обратный код
В этом коде связь между числом Х и его изображением в обратном коде - [Х]ок определяется равенством (7.2):
![\left[X\right]_{ОК}=\begin{cases} X, \text{если }X\geq0;\\ 2+X-2^{-n}, \text{если }X\leq0 \end{cases}](/sites/default/files/tex_cache/f47223159caba6d7f26ed53c2ca190ae.png) |
( 7.2) |
При Х ≥ 0:
[Х]ок = 2 + Х - 2-n = 2 - |X| - 2-n = 2 - 2-n + X.
Запишем это выражение в несколько другом виде.
Таким образом, для отрицательного числа получение обратного кода заключается в присвоении знаковому разряду кода 1 и замене в цифровой части числа 0 на 1, а 1 на 0 (выполняется ![\left[1,\overline{x}_1...\overline{x}_n\right]_{ДК}+2^{-n}](/sites/default/files/tex_cache/6d312e7da3d0001998a98ef29141b858.png) ).
).
При преобразовании от обратного кода к прямому от обратного кода числа берется обратный код.
Методика алгебраического суммирования в обратном коде при представлении исходных чисел и суммы в прямом коде
При суммировании чисел в обратном коде могут встретиться четыре возможные комбинации.
- Х > 0 и Y > 0, а X + Y < 1. В данном случае обращение к обратному коду не приводит к специфике выполнения операции, так как [Х > 0]ок + [Y > 0]ок = X + Y.
- Х > 0, Y < 0 и X + Y > 0.
[Х]ок + [Y]ок = X + 2 + Y - 2-n - предварительный результат.
Т.к. X + Y > 0, то действительный результат равен X + Y. Для того чтобы от предварительного результата перейти к действительному, необходима коррекция: вычесть 2 и прибавить 2-n к предварительному результату, т.е. в предварительном результате исключается 1 в разряде с весом 21, что равноценно вычитанию 2, и эту же единицу направляем в младший разряд предварительного результата, что равноценно прибавлению 2-n.
- Х > 0, Y < 0 и X + Y < 0.
[Х]ок + [Y]ок = X + (2 + Y - 2-n). Этот результат соответствует правильному, так как согласно условию X + Y < 0. Следовательно, [X + Y < 0]ок = 2 + (X + Y) - 2-n.
- Х < 0, Y < 0 и |Х + Y| < 1.
[X]ок + [Y]ок = (2 + X - 2-n ) + (2 + Y - 2-n ) - предварительный результат.
Правильный результат [(X + Y) < 0]ок = 2 + Х + Y - 2-n.
Это определяет необходимость выполнения коррекции предварительного результата, которая аналогична рассмотренной в случае 2, т.е. вычесть 2 и прибавить 2-n к предварительному результату.
При суммировании в обратном коде чисел разных знаков возможно получение X + Y = 0. Здесь методика суммирования обратных кодов исходных чисел не изменяется, а результат получается в виде 1,1 . . .1. Например,
Получили обратный код отрицательного нуля [- 0,0 . . . 0 ]ок = 1,1 ... 1. Такой результат согласуется с формулой (7.2), где указано, что X = 0 может иметь двоякое изображение: код положительного нуля и код отрицательного нуля.