|
Мне нужно изучить математическую статистику с нуля для обработки данных на компьютере. Читаю уже вторую лекцию, но пока ничего даже отдалённо близкого к моей цели не нахожу. Есть ли математическая статистика в дальнейших лекциях? Или я зря теряю время на изучение этого курса? У меня крайне ограниченный временной срок - я не могу терять время на самостоятельную проверку моего вопроса посредством изучения данного курса. |
Индексы в статистике
10.1. Понятие и виды статистических индексов
Каждый месяц Росстат в публикациях приводит большое количество разнообразнейших индексов, которые помогают лучше понять текущее состояние и развитие экономики страны. Индексы относятся к одним из самых распространенных видов статистических показателей. Наиболее известный и упоминаемый среди них - индекс потребительских цен, являющийся индикатором изменения цен и уровня жизни населения. Даже не экономист знает, что его значение, превышающее 100%, означает рост цен. Существует множество других статистических индексов, которые измеряют интенсивность изменения других важнейших социально-экономических явлений и процессов, например, объема ВВП, инвестиций в основной капитал, товарооборота, валютных курсов, уровней процентных ставок и т.д.
Общее определение индексов как статистических показателей можно сформулировать следующим образом.
Индексы - это относительные величины, которые выражают соотношение уровней социально-экономических явлений и используются для решения таких задач, как:
- обобщающая характеристика изменения одноименного показателя по разнородной совокупности во времени (индексы динамики), в пространстве (территориальные индексы) или по сравнению с некоторым заданным уровнем (например, планируемым или нормативным - индексы выполнения плана);
- анализ влияния отдельных факторов на изучаемое явление;
- оценка динамики среднего показателя по однородной совокупности, в том числе за счет изменений ее структуры.
Но не все относительные величины являются индексами. Отличительной чертой индексного метода является возможность проследить изменение непосредственно несоизмеримых отдельных элементов сложного явления в едином показателе. В качестве примера можно привести индекс потребительских цен, который в одной числовой характеристике представляет изменение цен на огромное множество товаров, предлагаемых покупателю. Другой пример: если предприятие выпускает несколько видов разнородной продукции, то нельзя получить общий объем выпуска прямым суммированием количества товаров по видам, и, следовательно, нельзя непосредственно с помощью простой относительной величины проследить общее изменение физического объема продукции. Индексный метод позволяет отдельные элементы сложного экономического явления привести к соизмеримому виду и дать единую характеристику изменения явления в целом, в данном случае - изменения выпуска продукции.
Кроме характеристики интенсивности изменения самого явления, индексы могут выполнять и аналитическую функцию: на их основе определяют влияние различных факторов на развитие явления. Например, при формировании товарооборота можно проследить прирост его объема за счет индивидуальных изменений цен на товары и изменений в объеме продаж.
На основе индексов проводится оценка изменения средних показателей по однородной совокупности, например средней цены товара, продаваемого в разных регионах, в том числе за счет непосредственно роста уровня цен и за счет изменения структуры продаж.
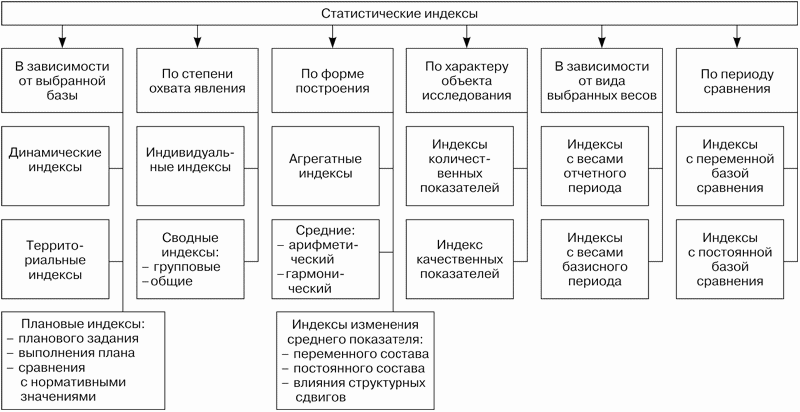
Статистические индексы классифицируются по следующим направлениям (рис. 10.1):
- выбранной в знаменателе индекса базе сравнения;
- степени агрегирования (или охвата) явления;
- форме построения сводных индексов;
- характеру исследуемой величины;
- виду весов, выбранных в индексе;
- периоду сравнения.
Экономическое содержание выбранной базы сравнения позволяет провести деление всех индексов на динамические, территориальные и индексы сравнения с плановыми (нормативными) значениями показателей.
Последняя группа включает в себя индексы планового задания [показывают степень увеличения (снижения) показателя, предусмотренную планом], индексы выполнения плана (показывают соотношение между фактическим значением показателя и его плановым уровнем), индексы сравнения с нормативными значениями (например, индексы выполнения норм расходов материала).
По степени агрегирования, или охвата явления, индексы делятся на индивидуальные и сводные. Индивидуальный индекс характеризует изменение показателя у отдельной единицы совокупности (например, изменение цены на принтеры определенной марки). Сводный индекс выступает в качестве обобщенной характеристики изменения показателя в целом по всей совокупности разнородных единиц (изменение цен в целом на принтеры всех видов).
Сводные индексы, в свою очередь, делятся на общие и групповые (субиндексы). Общие показывают изменение сложного явления в целом в рамках исследуемой совокупности, групповые - ее части. Например, если в качестве общего взять индекс потребительских цен, то субиндексом может являться индекс цен на продовольственные товары.
10.2. Индивидуальные индексы: правила их построения и анализа
Индивидуальный индекс представляет собой относительный показатель, характеризующий изменение отдельного элемента сложного экономического явления.
Методика исчисления индивидуальных индексов динамики социально-экономических показателей подобна методике расчета относительных величин: сравнивается абсолютное значение показателя в текущем и базисном периоде.
Величина, изменение которой изучается с помощью индекса, называется индексируемой величиной.
В индексной методологии принята следующая система обозначений:
q0, q1 - количество единиц (или физический объем) продукции (товаров) в натуральных единицах измерения;
p0, p1 - цена единицы продукции (товара);
z0, z1 - себестоимость единицы продукции;
t0, t1 - затраты рабочего времени на производство единицы продукции (трудоемкость продукции);
w0, w1 - количество продукции, выработанной одним работником в единицу времени (производительность труда);
Т1 и Т0 - затраты труда на производство продукции (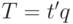 ).
).
Подстрочные обозначения "0" и "1" показывают временной период. Период времени, по отношению к которому производят сравнение, называют базисным и обозначают через "0", а период, сравниваемый с базисным, - отчетным и обозначают его через "1".
Приведем примеры построения индивидуальных индексов:
- индивидуальный индекс цен рассчитывается так:

Он показывает, как цена на данный товар в текущем периоде изменилась по сравнению с ценой этого же товара в базисном периоде;
- индивидуальный индекс физического объема имеет вид

Он позволяет сравнить физические объемы товарооборота (или производства продукции).
Аналогичным образом строятся индивидуальные индексы сравнения с плановыми или нормативными значениями, например индекс выполнения плана по объему продукции
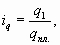
где qпл - количество единиц данного вида продукции, предусмотренное планом.
В числителе и знаменателе территориальных индексов находятся значения показателя, относящиеся к двум сравниваемым территориям, например индивидуальный территориальный индекс цен на определенный товар будет иметь вид
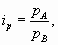
где рА, рВ - цена данного товара соответственно на территориях А и В.
Любой индекс может быть выражен в виде простого кратного отношения или в процентах. В первом случае он показывает, во сколько раз изменилась количественная характеристика экономического явления: его значение больше 1 свидетельствует об увеличении величины рассматриваемого показателя, меньше 1 - о снижении его уровня. Если индекс выразить в процентах и вычесть из него 100%, станет известно, на сколько процентов изменился показатель, характеризующий явление: отрицательное значение покажет процент снижения показателя, положительное - процент его увеличения.
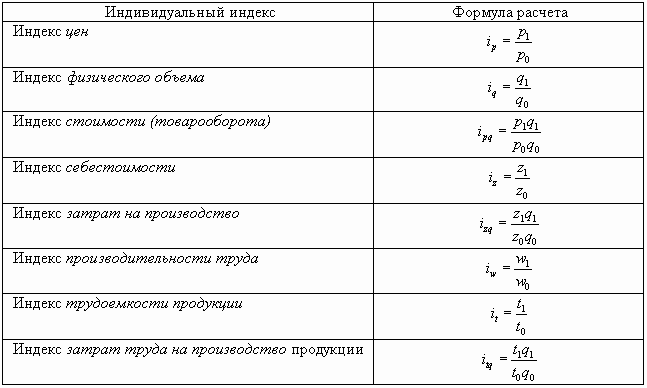
Ниже представлены формулы расчета индивидуальных индексов наиболее часто используемых экономических показателей.
Пример 10.1. Магазин продал 1800 кг товара "А" по цене 210 руб. за килограмм в июле, а в июне - 1600 кг этого же товара по цене 200 руб. Определим индивидуальные индексы:
- индивидуальный индекс физического объема реализованной продукции

- индивидуальный индекс цен
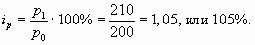
На основе проведенных расчетов можно сделать вывод, что в июле по сравнению с июнем объем реализации товара "А" увеличился в 1,125 раза, или на 12,5%, а цена этого товара - в 1,05 раза, или на 5%.