|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Использование угроз при формировании сделки
Угрозы в сделках с побочными платежами
Продолжим обсуждение последнего примера. Введение механизма побочных
платежей привело к тому, что выигрыш v+ второй стороны
в сделке (15.29) с побочными платежами оказывается меньше, чем ее выигрыш 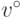 в сделке (14.18)
без побочных платежей (ср. расположение точек (u+,v+)
и
в сделке (14.18)
без побочных платежей (ср. расположение точек (u+,v+)
и  на рис. 3.9).
Выигрыш первой стороны, однако, увеличился
на рис. 3.9).
Выигрыш первой стороны, однако, увеличился 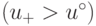 .
В такой ситуации вторая сторона могла бы настаивать на том,
что она согласует лишь такую сделку (u+,v+) с побочными
платежами, при которой от введения побочных платежей выигрывают обе
стороны, т.е. выполняются условия
.
В такой ситуации вторая сторона могла бы настаивать на том,
что она согласует лишь такую сделку (u+,v+) с побочными
платежами, при которой от введения побочных платежей выигрывают обе
стороны, т.е. выполняются условия

Принятие этих условий обеими сторонами означает, что допустимыми вариантами становятся сделки из множества
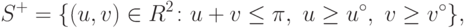 |
( 16.1) |
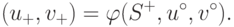 |
( 16.2) |
 .
.Фактически, схемы (15.28), (15.29) и (16.1), (16.2)
соответствуют разному поведению сторон при
согласовании сделки. Основным аргументом каждой стороны, настаивающей
на своем предложении, является отказ от сотрудничества. Такой отказ,
как уже отмечалось, ограничивает гарантированные выигрыши сторон P1 и P2 максиминными значениями u*
и v*, соответственно,
из (14.7) и (14.10). Тем не менее, стороны
могут пойти на эти (или даже большие) потери с тем, чтобы другая сторона
также понесла потери и стала более сговорчивой. Таким образом, возможен
стиль поведения, при котором сторона P1 угрожает стороне P2 отказом от кооперации и применением некоторой (в общем случае
смешанной) стратегии  , если ее пожелания не будут
учтены. Аналогично, сторона P2 может объявить свою стратегию угрозы
, если ее пожелания не будут
учтены. Аналогично, сторона P2 может объявить свою стратегию угрозы  .
.
В рассматриваемом примере сторона P2 может, например,
настаивать на
строительстве комплекса в ее районе Р2, заявляя, что в любом случае она
будет реализовывать свои средства только в этом районе. Такое поведение
можно интерпретировать как объявление чистой стратегии угрозы j=2.
Допустим, что сторона P1 решила вести себя аналогично и объявила
о применении чистой стратегии i=1 в случае отказа строить
комплекс в ее районе Р1. В результате при отказе от кооперации выигрыши сторон будут
определяться величинами 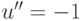 и
и 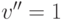 (см.
рис. 3.10). Т.е.
в ситуации отказа от кооперации положение стороны P1 оказывается хуже,
чем положение стороны P2. Это неравенство позволяет стороне P2 требовать бoльшую долю при разделе максимальной общей полезности
(см.
рис. 3.10). Т.е.
в ситуации отказа от кооперации положение стороны P1 оказывается хуже,
чем положение стороны P2. Это неравенство позволяет стороне P2 требовать бoльшую долю при разделе максимальной общей полезности  .
.
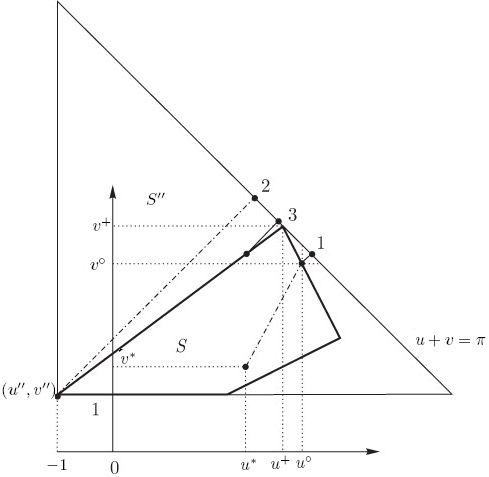
Отметим, что ключевым моментом в проведенном рассмотрении является признание сторонами реалистичности угроз, т.е. их готовность на самом деле использовать угрозы при отказе от сотрудничества, и отсутствие сомнений в том, что другая сторона поступит аналогично. При этих предположениях множество сделок, которые могут согласовать стороны (с учетом возможности побочных платежей), есть
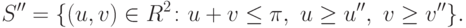 |
( 16.3) |
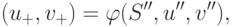 |
( 16.4) |
![u_{+} = \frac{1}{2}\left[\pi + (u'' - v'')\right],\quad
v_{+} = \frac{1}{2}\left[\pi - (u'' - v'')\right]\!.](/sites/default/files/tex_cache/fc052d75325f50b149fcd3eccc62a8be.png) |
( 16.5) |
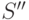 из (16.3)
и точка
из (16.3)
и точка 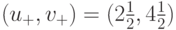 из (16.4) изображены на рис. 3.10 (точка имеет номер 2).
из (16.4) изображены на рис. 3.10 (точка имеет номер 2).