Тупики (deadlocks), методы предотвращения и обнаружения тупиков
Презентацию к данной лекции Вы можете скачать здесь.
Введение
Одна из важных задач операционной системы – распределение ресурсов компьютера между процессами. С данной задачей тесно связано понятие тупика (deadlock). В лекции введены базовые понятия, касающиеся распределения ресурсов и обнаружения тупиков. Рассмотрены следующие вопросы:
- Модель системы
- Граф распределения ресурсов
- Характеристика тупиков
- Обработка тупиков
- Предотвращение тупиков.
Проблема тупиков
Тупик (deadlock) – множество заблокированных процессов, каждый из которых владеет некоторым ресурсом и ожидает ресурса, которым владеет какой-либо другой процесс из этого множества.
Простой пример тупика легко смоделировать с помощью семафоров (см. "Методы синхронизации процессов" ). Пусть в системе есть два внешних устройства A и B, к которым обращаются два процесса P1 и P2. С каждым из внешних устройств с целью синхронизации связан семафор, которые будем обозначать также A и B.Семафоры изначально открыты. Пусть каждому из процессов необходимы оба устройства, но они обращаются к ним в противоположном порядке:
P1: wait(A); wait (B) P2: wait(B); wait (A).
В данном случае будет иметь место тупик: процесс P1, закрыв семафор A и заблокировав первое устройство, никогда не дождется, когда откроется семафор B,связанный со вторым устройством, так как его уже успел закрыть процесс P2.Аналогично, процесс P2 никогда не дождется, когда откроется семафор A.
Модель системы
Для описания и исследования подобных ситуаций введем формальную модель системы в общем виде. С помощью модели будем представлять информацию о запросах процессов к ресурсам, о фактическом владении процессов ресурсами и об освобождении ресурсов.
Пусть в системе имеется m видов ресурсов (например, процессор, память, устройства ввода-вывода). Будем обозначать типы ресурсов в системе R1, R2, … Rm.Пусть каждый тип ресурса Ri имеет Wi экземпляров.
Каждый процесс может использовать ресурс одним из следующих способов:
- запрос (request)
- использование (use)
- освобождение (release).
Тупик может возникнуть, если одновременно выполняются следующие четыре условия:
- взаимное исключение: только один процесс в каждый момент времени может получить доступ к ресурсу;
- удержание и ожидание: процесс, удерживающий один ресурс, ожидает приобретения других ресурсов, которыми обладают другие процессы;
- отсутствие прерываний:процесс может освободить ресурс только добровольно, когда завершит свою работу;
- циклическое ожидание: существует множество {P0, P1, … Pn},такое, что P0 ожидает ресурса, которым обладает P1; P1 ожидает ресурса, которым обладает P2 … Pn ожидает ресурса, которым обладает P0.
Граф распределения ресурсов
Введем в рассмотрение граф распределения ресурсов, состоящий из множества вершин V и множества дуг E. V подразделяется на два типа вершин: вершина-процесс и вершина-ресурс.Иначе говоря, V подразделяется на вершины типа P = {P1, P2, … ,Pn} множество всех процессов в системе, и вершины типа R = {R1, R2, … ,Rm}
Введем два типа дуг:
- дуга типа "запрос" (request edge) – направленная дуга типа Pi -> Rj
- дуга типа "присваивание" (assignment edge) – направленная дуга типа Ri -> Pj.
Смысл различных направленностей дуг в следующем. Если процесс претендует на какой-либо ресурс, то дуга проводится из вершины-процесса в вершину-ресурс. Когда же конкретная единица ресурса уже выделена какому-либо конкретному процессу, то дуга, в знак этой принадлежности, и проводится из вершины-ресурса в вершину процесс.
Уточним особенности вводимого графа и его вершин. В современной терминологии, граф данного вида называется reserved graph. Его вершина-процесс имеет обычный вид, а вершина-ресурс, соответствующая ресурсу Rj,состоит из Wj подвершин, каждая из которых обозначает конкретную единицу ресурса. В теории reserved graphs такие вершины иногда называют супервершинами (super-vertices).Таким образом, дуга запроса ведет из вершины-процесса в вершину-ресурс в целом, а дуга присваивания ведет из соответствующей подвершины вершины-ресурса в вершину-процесс.
Пример вершины-процесса приведен на рис. 13.1.
Пример (супер)вершины-ресурса с четырьмя экземплярами приведен на рис. 13.2: каждому экземпляру ресурса соответствует своя подвершина.
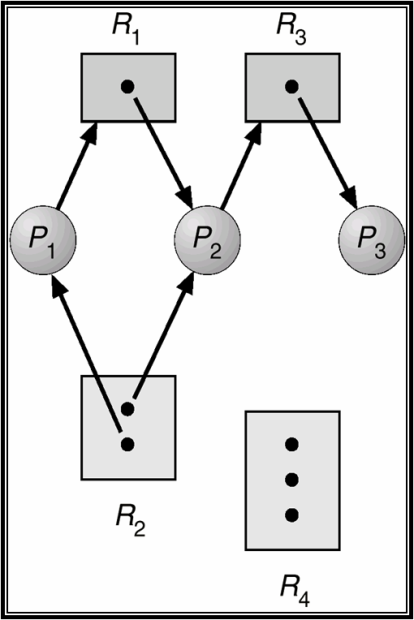
Пример графа распределения ресурсов приведен на рис. 13.3.
Данный граф изображает систему с тремя процессами и четырьмя видами ресурсов: ресурсы видов 1 и 3 имеют по одному экземпляру, ресурс вида 2 – два экземпляра, ресурс вида 4 – три экземпляра. Процесс 1 претендует на ресурс 1, который занят процессом 2. Процесс 2 претендует на ресурс 3, который занят процессом 3. Две единицы ресурса 2 отданы процессам 1 и 2. Ресурс 4 не распределялся (все три единицы свободны).