| Почему область решений была взята как многоугольник ОАВС. А как же точки (567;0) и (0;320). На мой взгляд, я бы выбрал многоугольник с точками О (567;0) (0;320). Ведь они являются областью пересечения двух ограничений |
Оптимизация производственных моделей
Структура производственных моделей
Производственная математическая модель предназначена для формирования оптимального производственного плана или технологических операций при ограниченных временных, материальных, трудовых и производственных ресурсах [3]. Критерием оптимальности является получение максимума прибыли или минимума издержек. Само планирование состоит обычно в определении количества выпускаемой продукции или составляющих в пределах заданного ассортимента. Чтобы создать математическую модель производственной фирмы, надо определить следующие параметры:
- константы нормативных затрат материалов, труда и финансов;
- переменные решения;
- целевую функцию;
- запас ресурсов или продукции;
- параметры спроса на продукцию.
Оптимизация модели производственного плана состоит в поиске максимума (для прибыли) или минимума (для затрат) целевой функции при ограничении на спрос и ресурсы [4]. При оптимизации раскроя листовых материалов возникают важные для технологов вопросы минимизации отходов. При составлении смесей часто требуется выполнить ограничение сверху и снизу концентрации составляющих компонент.
Задача 2.1. Составление производственного плана
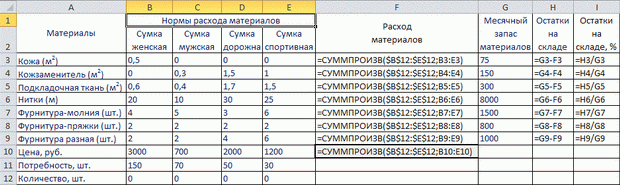
Фабрика выпускает сумки: женские, мужские, дорожные. Данные о материалах, используемых для производства сумок и месячный запас сырья на складе приведены в таблице.
| Материалы | Нормы расхода | Месячный запас материалов | |||
|---|---|---|---|---|---|
| Сумка женская | Сумка мужская | Сумка дорожная | Сумка спортивная | ||
| Кожа (м2) | 0,5 | 75 | |||
| Кожзаменитель (м2) | 0,3 | 1,5 | 1,0 | 150 | |
| Подкладочная ткань (м2) | 0,6 | 0,4 | 1,7 | 1,5 | 300 |
| Нитки (м) | 20 | 10 | 30 | 25 | 8000 |
| Фурнитура-молния (шт.) | 4 | 5 | 3 | 6 | 1500 |
| Фурнитура-пряжки (шт.) | 2 | 2 | 2 | 2 | 800 |
| Фурнитура разная (шт.) | 2 | 2 | 4 | 6 | 1000 |
По информации, полученной при изучении рынка продаж, ежемесячный спрос на продукцию фабрики составляет
- сумка женская — 150 шт. при оптовой цене 3000 руб.;
- сумка мужская — 70 шт. при оптовой цене 700 руб.;
- сумка дорожная — 50 шт. при оптовой цене 2000 руб.;
- сумка спортивная — 30 шт. при оптовой цене 1200 руб.
Отделом маркетинга были заключены договоры на поставки на следующий месяц.
Найти оптимальный план производства сумок каждого типа, обеспечивающий максимальную выручку при реализации продукции и обеспечивающий удовлетворение рыночного спроса.
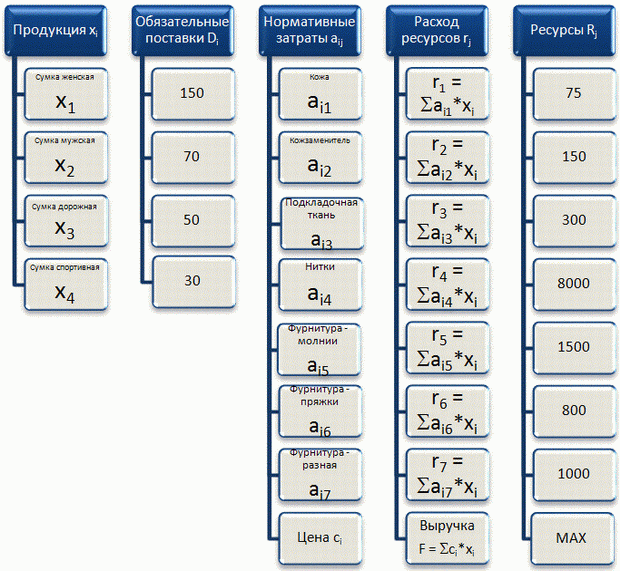
При разработке программ обычно составляют подробный алгоритм их реализации. Здесь также составим наглядную ментальную карту по исходным данным задачи. Ментальная карта должна проиллюстрировать основную формулу математической модели (рисунок 2.1):
Ментальную карту выполним в виде столбцов со списками данных (рисунок 2.2):
Продукцию мы представляем в виде вектора искомых переменных производственного плана

 . Составляющие этого вектора —
количество сумок данного типа, запланированные к производству в следующем месяце. Второй столбец представляет собой
вектор обязательных поставок
. Составляющие этого вектора —
количество сумок данного типа, запланированные к производству в следующем месяце. Второй столбец представляет собой
вектор обязательных поставок
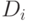 . Вектор поставок
. Вектор поставок 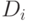 должен быть меньше
вектора переменных
должен быть меньше
вектора переменных  .
.
В третьем столбце представлена матрица нормативных коэффициентов 
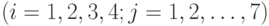 — удельных затрат материалов
на каждый вид сумки. Индексы определяют один из четырех видов продукции и один из семи видов ресурсов.
— удельных затрат материалов
на каждый вид сумки. Индексы определяют один из четырех видов продукции и один из семи видов ресурсов.
Вектор расхода материала  в четвертом столбце определяется
произведением матрицы нормативных коэффициентов
в четвертом столбце определяется
произведением матрицы нормативных коэффициентов
 на
вектор искомых значений переменных
на
вектор искомых значений переменных  .
Вектор расхода материала
.
Вектор расхода материала  не должен превышать вектор ресурсов
не должен превышать вектор ресурсов 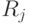 , составляющие которого приведены в последнем столбце.
, составляющие которого приведены в последнем столбце.
Целевая функция формируется скалярным произведением вектора цены
 на вектор искомых значений переменных
на вектор искомых значений переменных  .
Критерий оптимальности плана — получение
максимального значения выручки — целевой функции
.
Критерий оптимальности плана — получение
максимального значения выручки — целевой функции 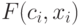 .
.
Подставляя в общие выражения исходные численные значения задачи, получим выражение для целевой функции:
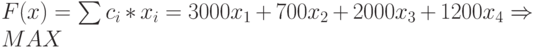
Оптимальному решению задачи отвечает максимальное значение целевой функции при следующих условиях и ограничениях:
| Выражение | Знак отношения | Ресурс | Примечание | |
|---|---|---|---|---|
 |
 |
150 | Выполнение договорных поставок | сумки женские |
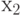 |
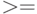 |
70 | сумки мужские | |
 |
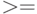 |
50 | сумки дорожные | |
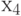 |
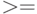 |
30 | сумки спортивные | |
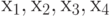 |
Целые | Доли сумок не выпускаются | ||
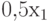 |
 |
75 | Ограничение на расход материалов | кожа |
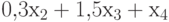 |
 |
150 | кожзаменитель | |
 |
 |
300 | подкладочная ткань | |
 |
 |
8000 | нитки | |
 |
 |
1500 | фурнитура-молнии | |
 |
 |
800 | фурнитура-пряжки | |
 |
 |
1000 | фурнитура-разная | |
Лишь после того, как мы разобрались в условиях задачи, можно приступить к формированию таблицы в MS Excel (рисунок 2.3). Заполним ячейки исходными данными. Искомые переменные (количество сумок каждого вида) поместим в ячейки строки 12. В ячейку F3 вставим формулу и протянем ее до ячейки F10. Напомним, что задание абсолютного адреса производится нажатием клавиши F4. Целевая функция помещается в ячейке F10. Это выручка, т.е. стоимость всех произведенных сумок.
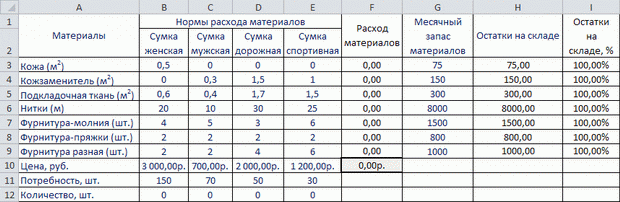
Отформатированная таблица представлена на рисунке 2.4. В ячейки для искомых переменных В12:Е12 можно вставлять, вообще говоря, любые числа. Программа выполнит подбор их числовых значений в соответствии с условиями задачи. Однако чаще всего в качестве начальных значений вводят 0 (как на рисунке 2.4) или 1 (как на рисунке 2.5).
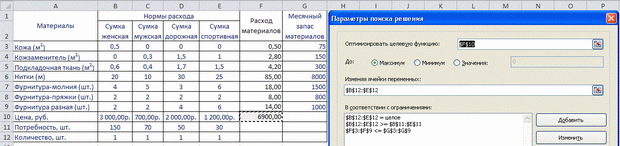
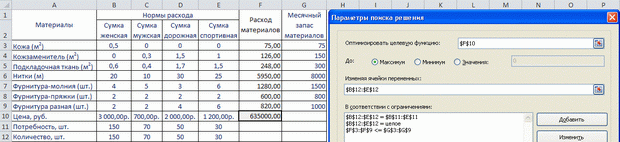
После вставки формул по команде Данные — Поиск решения вызовем диалог и заполним поля, как показано на рисунке 2.5. Адреса ячеек нужно не набирать вручную, а показывать мышью. Вызывать поля ограничений для записи нужно кнопкой "Добавить". На рисунке показано, что введены ограничения на целостность искомых переменных, на превышение выпуска продукции над обязательными поставками и на не превышение расхода материалов над запасами их на складе. Не отрицательность переменных учитывается в диалоге автоматически.
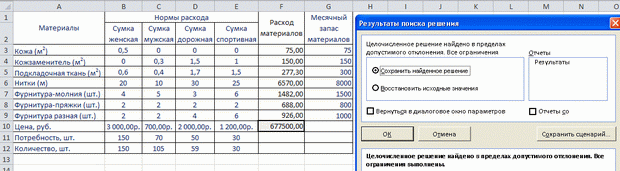
После выполнения команды "Найти решение" будет выдан результат расчета: значения искомых переменных и соответствующий расход материалов (рисунок 2.6):
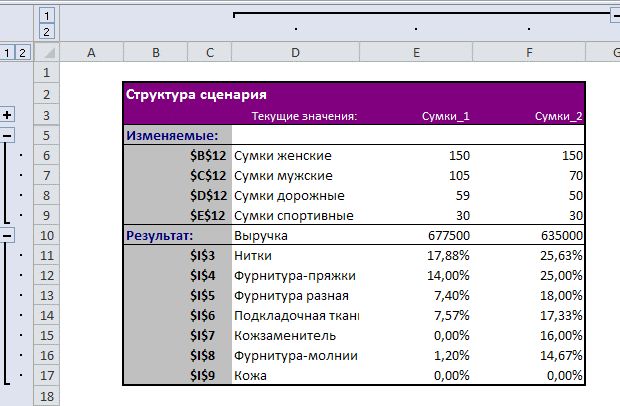
Таким образом, мы нашли, что максимально возможная выручка может составить 677500 руб. Для этого сверх договорных поставок мы должны изготовить 35 мужских сумок и 9 дорожных сумок. При этом на складе останется около 10% запаса материалов, кроме кожи и кожзаменителя, которые будут израсходованы полностью. Для сохранения результата нужно нажать кнопку "Сохранить сценарий", в диалоге дать имя сценарию "Сумки_1".
Оптимизация математической модели фактически закончена. Но теперь нужно перейти обратно от модели к реальной ситуации, т.е. принять управленческое решение. А что будет, если не удастся реализовать сумки, изготовленные сверх потребности? Ясно, что выручка будет равна только сумме, перечисленной от покупателей по договорным обязательствам. Тогда, может быть, и не изготавливать излишнюю продукцию? А сколько при этом останется материалов на складе? Руководитель предприятия на основе данного анализа должен иметь возможность принять решение о создании запасов как буферных (запас материалов для компенсации задержек в поставках), так и гарантийных (запас продукции для удовлетворения ожидаемого спроса).
Вернемся в диалоговое окно "Поиск решения". Изменим запись, приравняв в окне ограничений искомое количество продукции поставкам по договорам (рисунок 2.7):
Полученное решение оптимально — оно отвечает максимуму целевой функции и удовлетворяет заданным ограничениям. Сохраним второй сценарий под именем "Сумки_2".
А теперь подготовим графические материалы для отчета по составлению производственного плана. Представим остатки материалов на складе в конце следующего месяца для двух вариантов плана: для максимальной выручки и только для обязательных поставок.
По команде на ленте "Данные" — Анализ "что если" — Диспетчер сценариев — Отчет получим отчет по сценариям. Отредактируем отчет вручную по примеру, приведенному на рисунке 2.8:
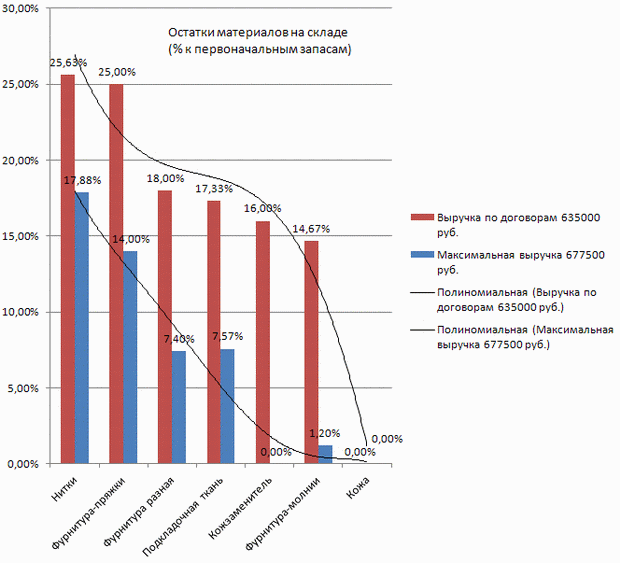
Для построения гистограмм остатков на складе проведем сортировку данных по убыванию и построим гистограммы по команде Вставка — Гистограмма (показаны на рисунке 2.9):
Таким образом, планируемая максимальная выручка в 677500 руб. обеспечена материальными ресурсами фабрики. Выпуск сумок только по обязательным договорным поставкам уменьшит выручку до 635000 руб. При этом остатки материалов на складе увеличатся.