НОУ ИНТУИТ | Введение в алгебру. Лекция 4: Кольцо многочленов от одной переменной

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 09.09.2007 | Доступ: платный | Студентов: 3 / 1 | Оценка: 4.35 / 3.78 | Длительность: 13:51:00

ISBN: 978-5-9556-0038-3

Тема: Математика

Специальности: Математик

Теги: beta, алгебра, алгоритмы, гомоморфизм групп, гомоморфизм группоидов, группоид, изоморфизм группоидов, инъекция, коэффициентами системы, моноид, полугруппа, расширенная матрица, старший коэффициент, элементы

|

Вам нравится? Нравится 69 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В данной лекции рассматриваются понятия колец с одной переменной. Приведены основные определения и свойства элементов кольца с одной переменной. Рассмотрен ряд характерных задач, доказаны основные теоремы, а также приведены задачи для самостоятельного рассмотрения

Кольцо многочленов от одной переменной

Пусть K - произвольное поле.

Под многочленом (ненулевым) от одной переменной x с коэффициентами из поля K будем понимать формальное выражение вида f(x)=a₀+a₁x+...+a_n-1x^n-1+a_nxⁿ (иногда удобнее записывать эту сумму одночленов a_ix^i в другом порядке: f(x)=a_nxⁿ+a_n-1x^n-1+...+a₁x+a₀ ), 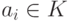$a_i\in K$ , $a_n\ne 0$ - старший коэффициент ( a_nxⁿ - старший член многочлена f(x) ), a₀ - свободный член, $n=\deg f(x)$ - степень ненулевого многочлена f(x) (нулевой многочлен - это f(x)=a₀=0 ).

Можно было вместо формальных выражений рассматривать счетные последовательности

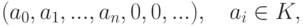
$(a_0,a_1,...,a_n,0,0,...),\quad a_i\in K,$

в которых почти все a_i (т. е. все, кроме конечного числа) равны нулю (нулевой многочлен - это последовательность, в которой все компоненты равны нулю).

Два многочлена f(x) и g(x) называются равными, если равны соответствующие коэффициенты при каждой степени x^k переменной x.

Через K[x] обозначим множество всех многочленов f(x) с коэффициентами из поля K.

На множестве K[x] введем операции сложения и умножения, для 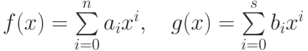$f(x)=\sum\limits^n_{i=0}a_ix^i,\quad g(x)=\sum\limits^s_{i=0}b_ix^i$ полагая $f(x)+g(x)=\sum\limits_{i\geq 0}d_ix^i,\quad f(x)g(x)=\sum\limits_{i\geq 0}t_ix^i$ , где $d_i=a_i+b_i,\quad t_i=\sum\limits_{\substack{k+l=i\\ 0\le k,l\le i}} a_kb_l$ .

Теорема 1.13.1. Множество K[x] с операциями сложения и умножения - коммутативное ассоциативное кольцо с единицей.

Доказательство.

Так как при сложении складываются коэффициенты при одной степени xⁱ, т. е. d_i=a_i+b_i, то ясно, что K[x] с операцией сложения - коммутативная группа.
Учитывая определение коэффициента
$t_i=\sum\limits_{\substack{k+l=i\\ 0\le k,l\le i}} a_kb_l,$
заключаем, что операция умножения коммутативна.
Пусть теперь
$h(x)=\sum\limits_{i\geq 0}c_ix^i.$
Тогда, подсчитывая коэффициенты при степени xⁱ в (f(x)g(x))h(x) и в f(x)(g(x)h(x)), видим, что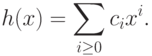
$\sum\limits_{u+m=i}\biggl(\,\sum\limits_{k+l=u}a_kb_l\biggr)c_m=\sum\limits_{k+l+m=i}a_kb_lc_m=\sum\limits_{k+v=i}a_k\biggl(\,\sum\limits_{l+m=v}b_lc_m\biggr).$
Итак, мы проверили ассоциативность умножения многочленов.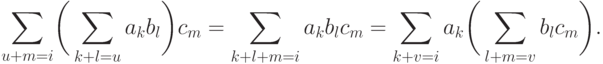

Ясно, что f(x)=1 (т. е. a₀=1 ) является нейтральным элементом для операции умножения.
Подсчитывая коэффициенты при степени xⁱ в (f(x)+g(x))h(x) и f(x)h(x)+g(x)h(x), видим, что
$\sum_{k+l=i}(a_k+b_k)c_l=\sum_{k+l=i}a_kc_l+\sum_{k+l=i}b_kc_l,$
т. е. установлен закон дистрибутивности в K[x].

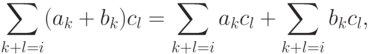
Замечание 1.13.2. Отображение $K\to K[x]$ , для которого $a\mapsto f(x)=a_0=a$ , является инъективным гомоморфизмом колец (т. е. получили вложение поля K в кольцо многочленов K[x] ).

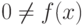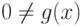Лемма 1.13.3. Пусть K - поле, $f(x),g(x)\in K[x]$ , $0\ne f(x)$ , $0\ne g(x)$ . Тогда

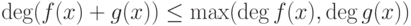а) $\deg(f(x)+g(x))\leq \max(\deg f(x),\deg g(x))$ .

б) $\deg(f(x)g(x))=\deg f(x)+\deg g(x)$ .

Доказательство.

а) Если $i>\max(\deg f(x),\deg g(x))$ , то c_i=a_i+b_i=0.

б) Если 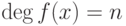$\deg f(x)=n$ , $\deg g(x)=s$ и i>n+s, то

$d_i= \sum\limits_{\substack{k+l=i\\ 0\le k,l\le i}}a_kb_l=0.$

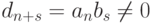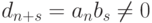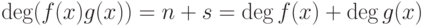При этом $d_{n+s}=a_nb_s\ne0$ (поскольку $a_n\ne 0$ , $b_s\ne 0$ и в поле K нет делителей нуля). Итак, $d_{n+s}=a_nb_s\ne 0$ - старший коэффициент многочлена f(x)g(x) - является произведением старших коэффициентов многочленов f(x) и g(x). Таким образом, $\deg(f(x)g(x))=n+s=\deg f(x)+\deg g(x)$ .

Следствие 1.13.4. Пусть K - поле. В кольце многочленов K[x] нет делителей нуля.

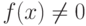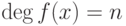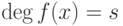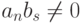Доказательство. Как мы видели, если $f(x)\ne 0$ , $\deg f(x)=n$ , $a_n\ne 0$ - старший коэффициент многочлена f(x), $g(x)\ne0$ , $\deg f(x)=s$ , $b_s\ne 0$ - старший коэффициент многочлена g(x), то $a_nb_s\ne 0$ - старший коэффициент многочлена f(x)g(x), т. е. $f(x)g(x)\ne 0$ .

Следствие 1.13.5. Пусть K - поле. В кольце K[x] (как в любом кольце без делителей нуля) можно сокращать на ненулевой многочлен, т. е. из f(x)g(x)=f(x)h(x), 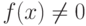$f(x)\ne 0$ , следует, что g(x)=h(x).

Дальше >>

Авторизоваться

Введение в алгебру

Кольцо многочленов от одной переменной

Кольцо многочленов от одной переменной

Вопросы и ответы