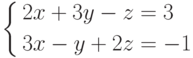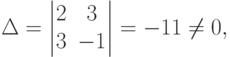НОУ ИНТУИТ | Введение в линейную алгебру. Лекция 5: Матричная запись системы. Метод Гаусса. Метод Крамера. Матричный способ

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.10.2007 | Доступ: платный | Студентов: 2 / 1 | Оценка: 4.09 / 3.28 | Длительность: 11:25:00

Тема: Математика

Специальности: Математик

|

Вам нравится? Нравится 45 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В лекции рассмотрено использование ранее изученных методов для поиска решений системы линейных уравнений

Правило Крамера

Основные задачи изучения системы (3.1), "лекции 3" :

Выяснить, является ли система (3.1) совместной или несовместной.
Если система (3.1) совместна, то выяснить, является ли она определенной и найти решения.

Далее рассмотрим, в частности, систему трех уравнений первой степени с тремя неизвестными.

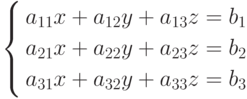$\left\{ \begin{aligned} a_{11}x+a_{12}y+a_{13}z=b_1 \\ a_{21}x+a_{22}y+a_{23}z=b_2 \\ a_{31}x+a_{32}y+a_{33}z=b_3 \end{aligned} \right.$

( 4.2)

Составим из коэффициентов при неизвестных системы (4.2) определитель этой системы

$\Delta= \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix}.$

Умножим обе части первого уравнения почленно на алгебраическое дополнение А₁₁ элемента а₁₁, второе уравнение - на алгебраическое дополнение А₂₁ элемента а₂₁, а третье - на алгебраическое дополнение А₃₁ элемента а₃₁.

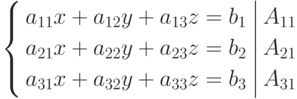
$\left\{ \begin{aligned} a_{11}x+a_{12}y+a_{13}z=b_1 \\ a_{21}x+a_{22}y+a_{23}z=b_2 \\ a_{31}x+a_{32}y+a_{33}z=b_3 \end{aligned} \right. \left| \begin{aligned} A_{11} \\ A_{21} \\ A_{31} \end{aligned} \right.$

Сложим все три полученных уравнения, умножив предварительно на соответствующие алгебраические дополнения, получим

$\begin{gathered} (a_{11}A_{11}+a_{21}A_{21}+a_{31}A_{31})x + (a_{12}A_{11}+a_{22}A_{21}+a_{32}A_{31})y + \\ +(a_{13}A_{11}+a_{23}A_{21}+a_{33}A_{31})z = b_1 A_{11}+b_2 A_{21}+b_3 A_{31} . \end{gathered}$

( 4.3)

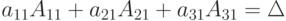Коэффициенты при y и z в силу свойства определителя (см. "лекц. 1" , теорема 2) равны нулю, а коэффициент при х на основании тех же свойств (см. "лекц. 1" , теорема 1) равен $\Delta$ , т.е. $a_{11}A_{11}+a_{21}A_{21}+a_{31}A_{31}=\Delta$ , поэтому равенство (4.3) примет вид:

$\Delta x = \Delta_x ,$

( 4.4)

$\text{где} \quad \Delta_x= \begin{vmatrix} b_1 & a_{12} & a_{13} \\ b_2 & a_{22} & a_{23} \\ b_3 & a_{32} & a_{33} \end{vmatrix} =b_1 A_{11}+b_2 A_{21}+b_3 A_{31} .$

( 4.5)

Заметим, что определитель $\Delta _{х}$ получается из определителя $\Delta$ путем замены коэффициентов а₁₁, а₂₁, а₃₁ при неизвестном х свободными членами или замены первого столбца $\Delta$ коэффициентов при искомом х столбцом свободных членов. Аналогично получаются другие равенства:

$\Delta y = \Delta_y , \quad \Delta z = \Delta_z ,$

( 4.6)

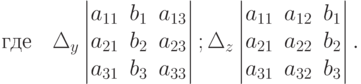
$\text{где} \quad \Delta_y \begin{vmatrix} a_{11} & b_1 & a_{13} \\ a_{21} & b_2 & a_{23} \\ a_{31} & b_3 & a_{33} \end{vmatrix}; \Delta_z \begin{vmatrix} a_{11} & a_{12} & b_1 \\ a_{21} & a_{22} & b_2 \\ a_{31} & a_{32} & b_3 \end{vmatrix}.$

Определители 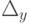$\Delta _{y}$ и $\Delta _{z}$ получают из определителя системы $\Delta$ заменой второго и третьего столбцов $\Delta$ коэффициентов при y и z столбцом свободных членов.

Рассмотрим следующие случаи.

$\Delta \ne 0$ . Тогда из равенств (4.4) и (4.5) находим решение системы (2) как
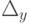$x=\frac{\Delta_x}{\Delta}; \; y=\frac{\Delta_y}{\Delta}; \; z=\frac{\Delta_z}{\Delta},$ ( 4.7)
которые называют формулами Крамера.
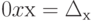$\Delta=0, \text{ а } \Delta_x^2 + \Delta_y^2 + \Delta_z^2 > 0$ . Тогда по крайней мере один из $\Delta _{х}$ , $\Delta _{y}$ или $\Delta _{z}$ отличен от нуля и система (4.2) не имеет решения (система несовместна), что можно показать. Пусть, например, $\Delta _{х}\ne 0$ . Тогда равенство из (4.4) получаем $\Delta х = \Delta _{х}$ или $0xх = \Delta _{х}$ , что невозможно.
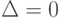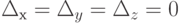$\Delta =0$ и $\Delta _{х} = \Delta _{y} = \Delta _{z} = 0$ . Тогда система (4.2) либо не имеет решения, либо имеет бесконечное множество решений.

Пример 1. Решить систему

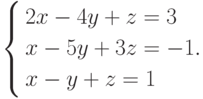
$\left\{ \begin{aligned} & 2x-4y+z=3 \\ & x-5y+3z=-1 \\ & x-y+z=1 \end{aligned}. \right.$

Решение. Вычислим все определители.

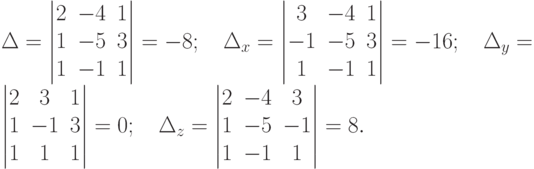
$\Delta= \begin{vmatrix} 2 & -4 & 1 \\ 1 & -5 & 3 \\ 1 & -1 & 1 \end{vmatrix} =-8; \quad \Delta_x= \begin{vmatrix} 3 & -4 & 1 \\ -1 & -5 & 3 \\ 1 & -1 & 1 \end{vmatrix} =-16; \quad \Delta_y= \begin{vmatrix} 2 & 3 & 1 \\ 1 & -1 & 3 \\ 1 & 1 & 1 \end{vmatrix} =0; \quad \Delta_z= \begin{vmatrix} 2 & -4 & 3 \\ 1 & -5 & -1 \\ 1 & -1 & 1 \end{vmatrix} =8.$

Так как 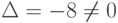$\Delta = -8 \ne 0$ , то данная система имеет единственное решение, которое найдем по формулам Крамера (4.7):

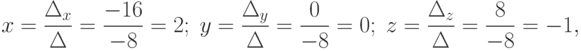
$x=\frac{\Delta_x}{\Delta}=\frac{-16}{-8}=2;\;y=\frac{\Delta_y}{\Delta}=\frac{0}{-8}=0;\;z=\frac{\Delta_z}{\Delta}=\frac{8}{-8}=-1,$

т.е. (2, 0, -1) - искомое решение системы.

Пример 2. Решить систему

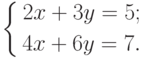
$\left\{ \begin{aligned} 2x+3y=5; \\ 4x+6y=7. \end{aligned} \right.$

Решение. Вычислим определители

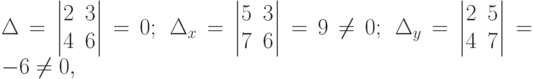
$\Delta= \begin{vmatrix} 2 & 3 \\ 4 & 6 \end{vmatrix} =0; \; \Delta_x= \begin{vmatrix} 5 & 3 \\ 7 & 6 \end{vmatrix} =9 \ne 0; \; \Delta_y= \begin{vmatrix} 2 & 5 \\ 4 & 7 \end{vmatrix} =-6 \ne 0 ,$

т.е. система решений не имеет (случай 2)

Пример 3. Решить систему

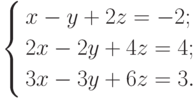
$\left\{ \begin{aligned} &x-y+2z=-2; \\ &2x-2y+4z=4; \\ &3x-3y+6z=3. \end{aligned} \right.$

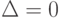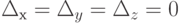Решение. Нетрудно убедиться в том, что $\Delta = 0$ и $\Delta _{х} = \Delta _{y} = \Delta _{z} = 0$ . Данная система не имеет решений, так как первое и третье уравнения противоречивы. Если умножить первое уравнение на 3 и вычесть из полученного уравнение третье, то придем к ложному равенству 0 = 3.

Пример 4. Решить систему

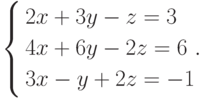
$\left\{ \begin{aligned} &2x+3y-z=3 \\ &4x+6y-2z=6 \\ &3x-y+2z=-1 \end{aligned}. \right.$

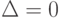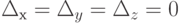Решение. Нетрудно убедиться в том, что $\Delta = 0$ и $\Delta _{х} = \Delta _{y} = \Delta _{z} = 0$ . Так как второе уравнение получается из первого умножением на 2, то данная система равносильна системе двух уравнений относительно трех неизвестных

$\left\{ \begin{aligned} &2x+3y-z=3 \\ &3x-y+2z=-1 \end{aligned} \right.$

Так как

$\Delta= \begin{vmatrix} 2 & 3 \\ 3 & -1 \end{vmatrix} = -11 \ne 0,$

то можно найти решение последней системы

$\left\{ \begin{aligned} &2x+3y=z+3 \\ &3x-y=-2z-1 \end{aligned} \right.$

в которой переменная z является свободной, и, следовательно, исходная система имеет бесконечное множество решений, которое можно найти либо по формулам Крамера, либо методом исключений. В результате получим (-5z/11; (7z+11)/11; z), где z может принимать произвольные значения.

Дальше >>

Авторизоваться

Введение в линейную алгебру

Матричная запись системы. Метод Гаусса. Метод Крамера. Матричный способ

Правило Крамера

Вопросы и ответы