|
Это в лекции 3. |
Логика предикатов и базы данных
Реляционные базы данных
Большинство современных промышленных баз данных являются реляционными - данные в них представляют конечные отношения (relations), которые хранятся в таблицах. Схема отношения R(A1,A2, ..., An) включает имя отношения R и список его атрибутов A1,A2, ..., An. Вообще говоря, атрибуты в схеме отношения считаются неупорядоченными, т.е. являются не списком, а множеством. Но мы будем считать, что их порядок в схеме является "стандартным". Для каждого атрибута Ai определено множество dom(Ai) его допустимых значений. Схема базы данных состоит из перечня схем отношений, входящих в эту базу. В приложениях отношения чаще называют таблицами, их атрибуты - столбцами, строки таблиц - кортежами или записями, а их элементы - полями. В каждый момент времени состояние базы данных (ее экземпляр) - это набор (конечных) таблиц имеющих соответствующие схемы.
Пример 8.1. Пусть, например, база данных со сведениями о сотрудниках некоторой организации имеет схему: Сотрудники(Номер, ФИО, Отдел, Должность, Оклад), Комнаты(НомерСотрудника, Этаж, НомерКомнаты). Рассмотрим некоторый экземпляр этой базы данных.
| Номер | ФИО | Отдел | Должность | Оклад |
|---|---|---|---|---|
| 1 | Иванов А.А. | торговый | менеджер | 7000 |
| 2 | Сидоров Н.П. | плановый | экономист | 5000 |
| 3 | Сидорова М.И. | торговый | зав.складом | 6000 |
| 4 | Ольгина Н.А. | плановый | экономист | 5500 |
| 5 | Горев С.В. | плановый | зав.отделом | 10000 |
С точки зрения логики предикатов, этот экземпляр не что иное, как некоторая конечная система сигнатуры  с основным множеством, включающим строки и числа из таблиц. Первая из приведенных таблиц задает интерпретацию предиката Сотрудники(5), а вторая - интерпретацию предиката Комнаты(3).
с основным множеством, включающим строки и числа из таблиц. Первая из приведенных таблиц задает интерпретацию предиката Сотрудники(5), а вторая - интерпретацию предиката Комнаты(3).
Каждому отношению базы данных со схемой R(A1, ..., An) мы сопоставим n -местный предикат с тем же именем и n одноместных предикатов Ai(x) (i=1, ..., n), выражающих принадлежность объекта x области dom(Ai) допустимых значений атрибута Ai. Следовательно, кортеж (a1, ... , an) принадлежит отношению R тогда и только тогда,
когда истинна формула 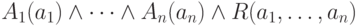 .
Множество таких предикатов для всех отношений базы данных и стандартных отношений,
определенных на областях ее атрибутов (обычно это отношения равенства и порядка: =, <, <=, >, >= ), образуют сингатуру базы данных.
.
Множество таких предикатов для всех отношений базы данных и стандартных отношений,
определенных на областях ее атрибутов (обычно это отношения равенства и порядка: =, <, <=, >, >= ), образуют сингатуру базы данных.
Например, для приведенного выше отношения Сотрудники(5) предикаты-свойства соответствующих областей значений могут быть заданы следующим образом:
-
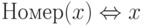 - целое число,
- целое число, -
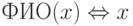 - строка символов длины <= 30,
- строка символов длины <= 30, -
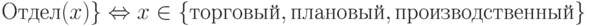 ,
, -
 - строка символов длины <= 80,
- строка символов длины <= 80, -
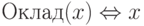 - целое число в интервале от 1000 до 100 000.
- целое число в интервале от 1000 до 100 000.
Каждый кортеж отношения Сотрудники удовлетворяет формуле  .
.
Ниже мы будем просто писать R(a1, ... , an), подразумевая, что значения ai
входят в соответствующие области dom(Ai). Каждая формула 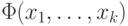 со свободными переменными x1, ... , xk
в сигнатуре базы данных определяет множество состояний, т.е. наборов значений
ее свободных переменных, на которых она истинна. Такое множество наборов можно рассматривать
как множество кортежей, которые входят в новое отношение
со свободными переменными x1, ... , xk
в сигнатуре базы данных определяет множество состояний, т.е. наборов значений
ее свободных переменных, на которых она истинна. Такое множество наборов можно рассматривать
как множество кортежей, которые входят в новое отношение 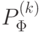 , определяемое формулой
, определяемое формулой 
Например, формула
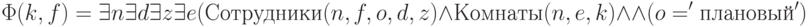
задает отношение 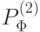 , определяющее список комнат сотрудников планового отдела:
, определяющее список комнат сотрудников планового отдела:
Отметим, что для конечных систем поиск значений свободных переменных формул логики предикатов, при которых они выполняются, и проверка истинности замкнутых формул производятся эффективно.
Реляционная алгебра
Для манипуляции отношениями Коддом в 1970 г. был предложен набор реляционных операторов, позволяющих по одним отношениям получать другие. Каждый такой оператор является функцией (вообще говоря, частичной), аргументами и значениями которой являются отношения. Из базовых реляционных операторов можно с помощью суперпозиции образовывать сложные термы. Совокупность получаемых таким образом операций над отношениями называется реляционной алгеброй.
В этом разделе мы рассмотрим семь основных реляционных операторов, введенных Коддом в качестве базиса реляционной алгебры, и покажем, как они выражаются в терминах логики предикатов.
Теоретико-множественные операции
Первую группу реляционных операторов представляют теоретико-множественные операции:
В
"лекции 1"
мы рассматривали все эти операции для множеств.
Особенности их использования в реляционной алгебре состоят в том, что
объединение, пересечение и вычитание применяются к отношениям, имеющим
одно и то же множество одинаково упорядоченных атрибутов.
Пусть имеются два таких отношения R(A1, ..., An) и S(A1, ..., An). Тогда результат их объединенния - это отношение 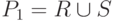 , содержащее все кортежи отношения R и
все кортежи отношения S (кортежи, содержащиеся и в R, и в S, входят в P
в одном экземпляре). Это отношение представляется формулой
, содержащее все кортежи отношения R и
все кортежи отношения S (кортежи, содержащиеся и в R, и в S, входят в P
в одном экземпляре). Это отношение представляется формулой  .
Результат пересечения - это отношение P2 = R \cap S, которое содержит кортежи, входящие и в R и
в S. Оно представляется формулой
.
Результат пересечения - это отношение P2 = R \cap S, которое содержит кортежи, входящие и в R и
в S. Оно представляется формулой 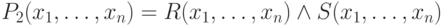 .
Результат разности P3= R - S включает кортежи из R, не входящие в S. Это отношение представляется формулой
.
Результат разности P3= R - S включает кортежи из R, не входящие в S. Это отношение представляется формулой  .
Декартово произведение P4= R x S отношений R(A1, ..., An) и S(B1, ..., Bm) содержит кортежи, которые составлены из
кортежей отношения R, продолженных кортежами отношения S. Список атрибутов P4 включает все атрибуты отношений R и S: (A1, ..., An, B1, ..., Bm).
Если у R и S имеются общие атрибуты, то они переименовываются. Обычно перед
именем атрибута общего атрибута Ai=Bj
помещается через точку имя его отношения, R.Ai и S.Bj.
Результат декартового произведения задается формулой
.
Декартово произведение P4= R x S отношений R(A1, ..., An) и S(B1, ..., Bm) содержит кортежи, которые составлены из
кортежей отношения R, продолженных кортежами отношения S. Список атрибутов P4 включает все атрибуты отношений R и S: (A1, ..., An, B1, ..., Bm).
Если у R и S имеются общие атрибуты, то они переименовываются. Обычно перед
именем атрибута общего атрибута Ai=Bj
помещается через точку имя его отношения, R.Ai и S.Bj.
Результат декартового произведения задается формулой 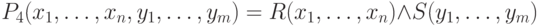 (мы предполагаем, что все переменные xi и yj разные).
(мы предполагаем, что все переменные xi и yj разные).
