|
Это в лекции 3. |
Логика предикатов и базы данных
Специальные реляционные операторы
К специальным реляционным операторам относятся:
- Выбор
- Проекция
- Соединение
- Деление
Оператор выбора, примененный к отношению R(A1, ..., An),
возвращает новое отношение P с тем же набором атрибутов, кортежи которого
составляют подмножество кортежей отношения R, удовлетворяющих некоторому
условию C. Это записывается как 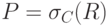 . Условие C представляет из себя булевскую
формулу, которая построена из элементарных условий, включающих имена атрибутов R
и константы. Примерами элементарных условий являются равенства вида Ai = Aj, Ai=a
и неравенства вида Ai <= Aj, Ai <= a, Ai >= a.
Тогда отношение P задается формулой
. Условие C представляет из себя булевскую
формулу, которая построена из элементарных условий, включающих имена атрибутов R
и константы. Примерами элементарных условий являются равенства вида Ai = Aj, Ai=a
и неравенства вида Ai <= Aj, Ai <= a, Ai >= a.
Тогда отношение P задается формулой 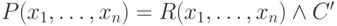 , где формула C' получена
из условия C заменой имен атрибутов Ai на имена соответствующих переменных xi.
, где формула C' получена
из условия C заменой имен атрибутов Ai на имена соответствующих переменных xi.
Например, оператору выбора  , выбирающему сотрудников с окладом
свыше 6000,
соответствует формула
, выбирающему сотрудников с окладом
свыше 6000,
соответствует формула 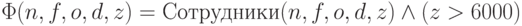 ,
задающая отношение
,
задающая отношение 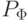 :
:
| Номер | ФИО | Отдел | Должность | Оклад |
|---|---|---|---|---|
| 1 | Иванов А.А. | торговый | менеджер | 7000 |
| 5 | Горев С.В. | плановый | зав.отделом | 10000 |
Оператор проекции, примененный к отношению R(A1, ..., An), возвращает
все кортежи этого отношения, из которых удалены значения атрибутов, не перечисленных
в списке параметров этой операции. Отношение P, являющееся проекцией R на подмножество атрибутов 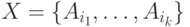 , записывается как
, записывается как 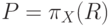 .
Пусть
.
Пусть  - это атрибуты отношения, не попавшие в X. Тогда проекция
задается формулой
- это атрибуты отношения, не попавшие в X. Тогда проекция
задается формулой 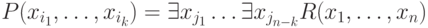 .
.
Например, оператору проекции  ,
составляющему список окладов сотрудников,
соответствует формула
,
составляющему список окладов сотрудников,
соответствует формула  , задающая
двуместное отношение
, задающая
двуместное отношение 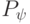 :
:
Оператор соединения применяется к двум отношениям и позволяет
соединять попарно их кортежи, удовлетворяющие определенным условиям.
В реляционной алгебре он представлен в нескольких формах.
Пусть R и S - это отношения со схемами R(A1, ..., An, B1, ..., Bm) и S(B1, ..., Bm, C1, ..., Ck) с общими атрибутами B1, ..., Bm.
Тогда естественное соединение 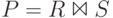 отношений R и S
содержит кортежи, которые составлены из
кортежей отношения R, продолженных кортежами отношения S. При этом соединяются
лишь пары кортежей
отношений R и S
содержит кортежи, которые составлены из
кортежей отношения R, продолженных кортежами отношения S. При этом соединяются
лишь пары кортежей  и
и  , имеющих одинаковые значения всех общих атрибутов B1, ..., Bm. Так как значения общих атрибутов совпадают они входят
в схему P по одному разу, т.е. P имеет схему P(A1, ..., An, B1, ..., Bm, C1, ..., Ck).
Нетрудно понять, что естественному соединению соответствует формула
, имеющих одинаковые значения всех общих атрибутов B1, ..., Bm. Так как значения общих атрибутов совпадают они входят
в схему P по одному разу, т.е. P имеет схему P(A1, ..., An, B1, ..., Bm, C1, ..., Ck).
Нетрудно понять, что естественному соединению соответствует формула 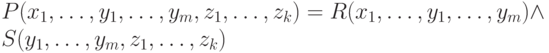 .
.
Пусть в дополнение к отношениям Сотрудники и Комнаты в базу данных входит отношение Оборудование:
Тогда отношение  определяет доступность
тех или иных аппаратов сотрудникам в их комнатах. Оно имеет схему Доступ (НомерСотрудника, Этаж, НомерКомнаты, Название) и представлено в следующей таблице:
определяет доступность
тех или иных аппаратов сотрудникам в их комнатах. Оно имеет схему Доступ (НомерСотрудника, Этаж, НомерКомнаты, Название) и представлено в следующей таблице:
| НомерСотрудника | Этаж | НомерКомнаты | Название |
|---|---|---|---|
| 3 | 2 | 17 | компьютер |
| 3 | 2 | 17 | принтер |
| 1 | 2 | 17 | компьютер |
| 1 | 2 | 17 | принтер |
| 5 | 3 | 7 | ксерокс |
Здесь соединение производится по двум общим атрибута м Этаж и НомерКомнаты. При этом в соединение не попали сведения о сотрудниках с номерами 2 и 7, в комнатах которых нет оборудования, и о принтере в комнате 25, так как в
ней нет сотрудников. Соответствующая формула имеет вид:  .
.
Другой вариант оператора соединения - тета-соединение 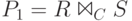 отношений R и S
содержит кортежи, которые составлены из
кортежей отношения R, продолженных кортежами отношения S, удовлетворяющими
условию C. Синтаксис этого условия такой же, как и у оператора выбора. Так как
в C могут входить не только равенства атрибутов, то атрибуты R и S с одинаковыми именами
входят в схему P1 дважды (обычно, как и в случае декартова произведения,
перед ними помещается через точку имя отношения ).
Оператор тета-соединения выражается через операторы выбора и декартового произведения:
отношений R и S
содержит кортежи, которые составлены из
кортежей отношения R, продолженных кортежами отношения S, удовлетворяющими
условию C. Синтаксис этого условия такой же, как и у оператора выбора. Так как
в C могут входить не только равенства атрибутов, то атрибуты R и S с одинаковыми именами
входят в схему P1 дважды (обычно, как и в случае декартова произведения,
перед ними помещается через точку имя отношения ).
Оператор тета-соединения выражается через операторы выбора и декартового произведения: 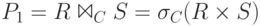 . Ему соответствует формула
. Ему соответствует формула 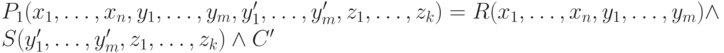 ,
в которой C' - это формула C, где вместо имен атрибутов подставлены имена соответствующих
переменных.
,
в которой C' - это формула C, где вместо имен атрибутов подставлены имена соответствующих
переменных.
Операторы реляционной алгебры можно соединять в сложные выражения, позволяющие выражать необходимые пользователям запросы. Например, чтобы получить список фамилий сотрудников с доступным каждому из них оборудованием, можно использовать выражение

Результат его вычисления представлен в следующей таблице:
| ФИО | Название |
|---|---|
| Иванов А.А. | компьютер |
| Иванов А.А. | принтер |
| Сидорова М.И | компьютер |
| Сидорова М.И | принтер |
| Горев С.В. | ксерокс |
Ее строки соответствуют парам значений переменных f,c, на которых истинна формула 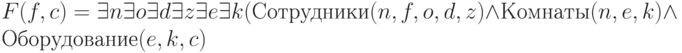 .
.
