Вычисления с использованием функций
Вычисления с использованием некоторых функций
Финансовые вычисления
Расчет амортизационных отчислений
Для расчета амортизационных отчислений необходимо знать, по крайней мере, три параметра:
- начальная стоимость имущества;
- остаточная стоимость по окончании эксплуатации;
- продолжительность эксплуатации.
Для расчета амортизационных отчислений могут быть использованы различные принципы и методики. В зависимости от этого могут быть применены и различные функции.
В простейшем случае амортизация разносится равномерно на каждый год эксплуатации имущества. При этом для расчета величины амортизационных отчислений используют функцию АПЛ.
Синтаксис функции:
АПЛ(А;В;С),
где
А - начальная стоимость имущества;
В - остаточная стоимость имущества;
С - продолжительность эксплуатации.
Например, приобретено оборудование стоимостью 100000 руб. Продолжительность эксплуатации оборудования - 8 лет. Остаточная стоимость - 12000 руб. Величина амортизационных отчислений составит 11000 руб. за каждый и любой год эксплуатации ( рис. 17.1).
Расчет суммы вклада (величины займа)
В простейших случаях для расчета можно использовать функцию БС. Эта функция вычисляет для будущего момента времени величину вклада, который образуется в результате единовременного вложения и/или регулярных периодических вложений под определенный процент. Эту же функцию можно использовать для вычисления возможной величины займа под определенный процент, при определенных регулярных периодических выплатах по погашению займа.
Синтаксис функции
БС(А;В;С;D;Е),
где
А - процентная ставка за период;
В - общее число платежей;
С - выплата, производимая в каждый период и не меняющаяся за все время выплаты;
D - требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент опущен, он полагается равным 0 (будущая стоимость займа, например, равна 0);
Е - число 0 или 1, обозначающее, когда должна производиться выплата. 0 или опущен - в конце периода, 1 - в начале периода.
При создании формулы следует устанавливать одинаковую размерность периода для процентной ставки и числа платежей. Например, если платежи производятся один раз в год, то и процентная ставка должна быть дана в годовом исчислении, а если платежи производятся ежемесячно, то должна быть задана месячная процентная ставка.
Все аргументы, означающие денежные средства, которые должны быть выплачены (например, сберегательные вклады), представляются отрицательными числами; денежные средства, которые должны быть получены (например, дивиденды), представляются положительными числами.
При создании формулы не обязательно указывать все аргументы функции. Вместо отсутствующего аргумента в строке формул должна быть точка с запятой.
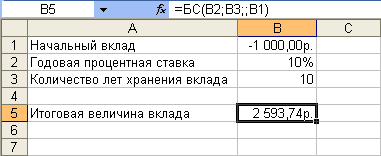
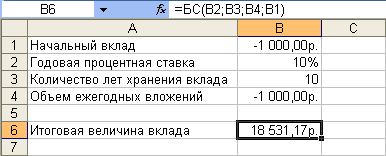
Например, необходимо рассчитать будущую сумму вклада в размере 1000 руб., внесенного на 10 лет с ежегодным начислением 10% ( рис. 17.2). Или будущую сумму вклада при тех же условиях, но с ежегодным внесением 1000 руб. ( рис. 17.3).
Результат вычисления: в первом случае - 2593,74 руб., во втором - 18531,17руб.
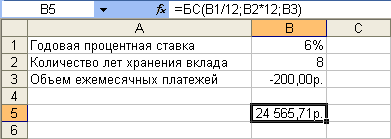
Или, необходимо рассчитать будущую сумму вклада при ежемесячном внесении 200 руб. в течение 8 лет с ежегодным начислением 6%. Начальный вклад равен 0 ( рис. 17.4).
Результат вычисления - 24 565, 71 руб.
Эту же формулу (см. рис. 17.4) можно использовать и для расчета величины возможного займа. Например, требуется рассчитать, какую сумму можно занять на 8 лет под 6% годовых, если есть возможность выплачивать ежемесячно по 200 руб. Результат будет тот же самый - 24 565,71 руб.