|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Системы с ожиданием
Мы рассмотрим те же самые два случая потоков нагрузки, о которых говорили в Лекциях 7 и 8.
-
Пуассоновский поток вызовов (бесконечное число источников) и экспоненциально распределенное время обслуживания ( PCT-I ). Эта самая важная система организация очереди называется Эрланговская система с ожиданием. Используя систему обозначений, которую мы введем позже в секции 13.1, назовем Эрланговскую систему с ожиданием -
 . В этой системе обслуженная нагрузка равна предложенной нагрузке, поскольку попытки вызова не блокируются. Положительная вероятность времени ожидания означает необходимость вычисления:
. В этой системе обслуженная нагрузка равна предложенной нагрузке, поскольку попытки вызова не блокируются. Положительная вероятность времени ожидания означает необходимость вычисления:- длины очереди;
- среднего времена ожидания;
- функции увеличения.
С этими параметрами мы будем иметь дело в секции 12.2. В секции12.3 будет показано, как для оптимизации системы может быть применен Принцип Мо. В секции 12.4. вычисляется распределение времени ожидания для основной дисциплины обслуживания - Первый Прибыл Первый обслужен ( FCFS * - First Come First Served).
- Ограниченное число источников и экспоненциально распределенное время обслуживания ( PCT-II ). Эта модель Пальма, называемая моделью восстановления машин, рассмотрена в секции 12.5. (проблема взаимного влияния машин) и широко применяется для того, чтобы планировать сети, например, компьютерные сети, терминальные сети. Модель восстановления машин оптимизирована в секции 12.6.
Система с ожиданием Эрланга M/M/n
Рассмотрим систему с ожиданием  . Она обслуживает Пуассоновский поток вызовов (
. Она обслуживает Пуассоновский поток вызовов (  ), имеет экспоненциальное время обслуживания (
), имеет экспоненциальное время обслуживания (  ) и n обслуживающих приборов при бесконечном числе мест ожидания. Состояние системы определяется как общее количество пользователей в системе (или в обслуживании, или ожидающих в очереди).
) и n обслуживающих приборов при бесконечном числе мест ожидания. Состояние системы определяется как общее количество пользователей в системе (или в обслуживании, или ожидающих в очереди).

Рис. 12.1. Диаграмма переходов состояний M/M/n системы с ожиданием, имеющей n серверов и неограниченное число мест ожидания.
Нас интересуют вероятности устойчивых состояний системы. В секции 7.4 дана диаграмма переходов между состояниями (рис.12.1). Принимая, что диаграмма находится в статистическом равновесии, получаем:
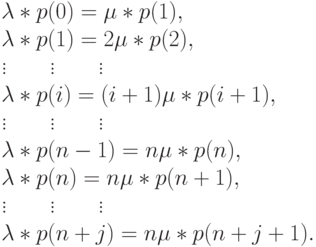 |
( 12.1) |
Если 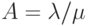 - это предложенная нагрузка, то мы имеем:
- это предложенная нагрузка, то мы имеем:
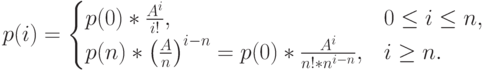 |
( 12.2) |
С помощью нормировки вероятностей состояний получаем:
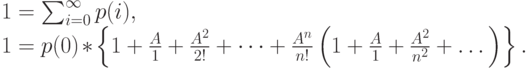
Внутренние фигурные скобки содержат геометрическую прогрессию с коэффициентом прогрессии  . Условие нормализации может быть выполнено только для:
. Условие нормализации может быть выполнено только для:
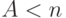 |
( 12.3) |
Статистическое равновесие получено лишь для  . Иначе очередь будет увеличиваться до бесконечности. Мы получаем значение
. Иначе очередь будет увеличиваться до бесконечности. Мы получаем значение  :
:
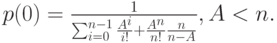 |
( 12.4) |
Уравнения (12.2) и (12.4) показывают вероятности устойчивых состояний.
Характеристики нагрузки систем с ожиданием
Для оценки производительности и рабочих характеристик системы нужно рассмотреть несколько характеристик. Они отражают вероятности устойчивых состояний.
C-формула Эрланга
Когда Пуассоновский поток вызовов не зависит от состояния системы, вероятность того, что произвольный вызов должен будет ждать обслуживания в очереди, равна пропорции времени, когда заняты все обслуживающие приборы ( свойство PASTA ). Время ожидания - случайная величина, которая обозначается  . Для произвольного поступления вызовов имеем:
. Для произвольного поступления вызовов имеем:
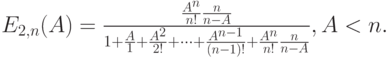 |
( 12.6) |
Эта вероятность ожидания зависит только от  , т.е.произведения
, т.е.произведения  и
и  . Формула имеет несколько названий: C-формула Эрланга, вторая формула Эрланга или формула Эрланга для систем с ожиданием. Она имеет различные обозначения в литературе:
. Формула имеет несколько названий: C-формула Эрланга, вторая формула Эрланга или формула Эрланга для систем с ожиданием. Она имеет различные обозначения в литературе:
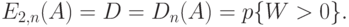
Клиенты либо обслуживаются немедленно, либо помещаются в очередь. Вероятность, что клиент обслуживается немедленно, равна:
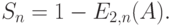
Обслуженная нагрузка  равняется предложенной нагрузке
равняется предложенной нагрузке  , так как ни одному вызову не отказывается в обслуживании, а процесс поступления вызовов - Пуассоновский процесс:
, так как ни одному вызову не отказывается в обслуживании, а процесс поступления вызовов - Пуассоновский процесс:
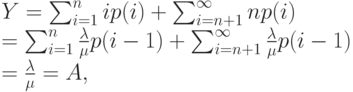 |
( 12.7) |
Здесь применено уравнение равновесия.
Длина очереди - случайная величина  . Вероятность наличия клиентов в очереди в случайной точке времени:
. Вероятность наличия клиентов в очереди в случайной точке времени:
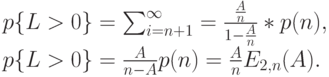 |
( 12.8) |
Здесь использовалось (12.5).
Числовая оценка
Формула подобна B-формуле (7.10) Эрланга, за исключением коэффициента 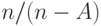 в последнем элементе. Поскольку существует очень точная рекурсивная формула для числовой оценки B-формулы Эрланга (7.29), можно использовать следующие отношения для того, чтобы получить числовые значения для C-формулы:
в последнем элементе. Поскольку существует очень точная рекурсивная формула для числовой оценки B-формулы Эрланга (7.29), можно использовать следующие отношения для того, чтобы получить числовые значения для C-формулы:
 |
( 12.9) |
где элемент 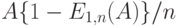 - средняя обслуженная нагрузка на канал в соответствующей системе с потерями. Для
- средняя обслуженная нагрузка на канал в соответствующей системе с потерями. Для 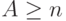 мы имеем
мы имеем  . Это - вероятность того, что все клиенты поставлены на ожидание. C-формула Эрланга может быть выражена B-формулой:
. Это - вероятность того, что все клиенты поставлены на ожидание. C-формула Эрланга может быть выражена B-формулой:
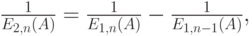 |
( 12.10) |
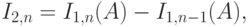 |
( 12.11) |
где  - инверсия вероятности (7.30).
- инверсия вероятности (7.30).
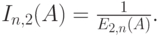
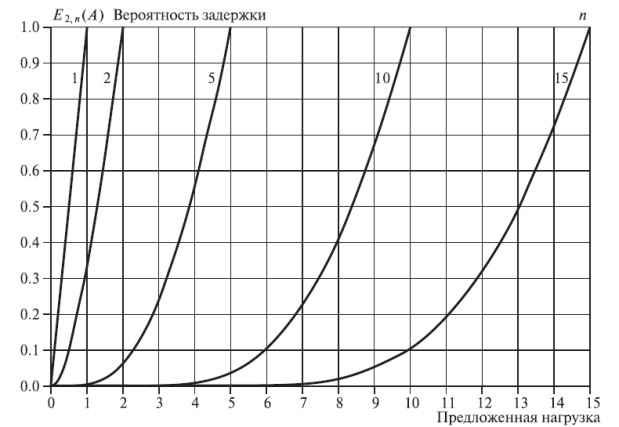
C-формула Эрланга была сведена в таблицу в Принципе Мо (Jensen, 1950 [50] ) и показана на рис.12.2.
Вероятность 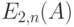 для положительного времени ожидания показана как функция предложенной нагрузки для различных значений числа обслуживающих приборов n.
для положительного времени ожидания показана как функция предложенной нагрузки для различных значений числа обслуживающих приборов n.
Средняя длина очереди
Мы должны отличать длину очереди в произвольный момент времени и длину очереди, когда есть клиенты, стоящие в очереди.
Средняя длина очереди в произвольный момент времени
Длина очереди  в произвольной момент времени называется виртуальной длиной очереди. Для произвольного клиента длина очереди определяется как свойство PASTA, т.е. Пуассоновский поток вызовов (математическое ожидание по времени = математическое ожидание по вызовам). Мы получаем среднюю длину очереди:
в произвольной момент времени называется виртуальной длиной очереди. Для произвольного клиента длина очереди определяется как свойство PASTA, т.е. Пуассоновский поток вызовов (математическое ожидание по времени = математическое ожидание по вызовам). Мы получаем среднюю длину очереди:
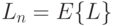 в произвольный момент времени:
в произвольный момент времени:
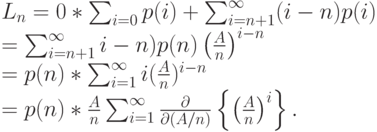
Поскольку  , ряд является равномерно сходящимся, оператор дифференцирования может быть вынесен за сумму:
, ряд является равномерно сходящимся, оператор дифференцирования может быть вынесен за сумму:
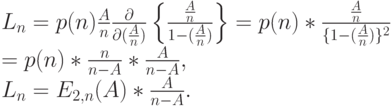 |
( 12.12) |
Средняя длина очереди может интерпретироваться как нагрузка, которую обслуживают места ожидания очереди, и поэтому она иногда называется нагрузкой времени ожидания.
Средняя длина очереди, со временем ожидания больше нуля
Математическое ожидание времени и в этом случае равно математическому ожиданию вызова. Условная средняя длина очереди будет:
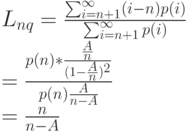 |
( 12.13) |
Применяя (12.8) и (12.12), получаем:

где  - случайная переменная, обозначающая длину очереди.
- случайная переменная, обозначающая длину очереди.
Средние времена ожидания
Здесь представляют интерес две характеристики:
- среднее время ожидания
 для всех клиентов;
для всех клиентов; - среднее времени ожидания w для клиентов, для которых время ожидания имеет положительное значение.
Первая является индикатором уровня обслуживания целой системы, тогда как вторая относится к задержанным вызовам.
Математические ожидания времени будут равны математическим ожиданиям по вызовам из-за свойства PASTA.
Среднее время ожидания для всех вызовов
Формула Литла говорит, что средняя длина очереди равна интенсивности прибытия, умноженной на среднее время ожидания:
 |
( 12.14) |
где 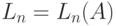 и
и  . Рассматривая процесс поступления вызовов, из (12.12) мы имеем:
. Рассматривая процесс поступления вызовов, из (12.12) мы имеем:
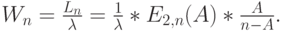
Поскольку 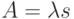 , где
, где  - среднее время обслуживания, мы имеем:
- среднее время обслуживания, мы имеем:
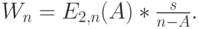 |
( 12.15) |
Среднее время ожидания для задержанных вызовов
Полное время ожидания является постоянным и может быть вычислено либо в среднем по всем клиентам ( 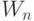 ), либо только по вызовам, для которых времена ожидания (
), либо только по вызовам, для которых времена ожидания ( 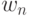 ) имеют положительные значения (3.20):
) имеют положительные значения (3.20):
 |
( 12.16) |
 |
( 12.17) |
Пример 12.2.1: Система организации очереди с одним обслуживающим прибором (M/M/1)
Эта система наиболее часто упоминается в литературе. Вероятности состояния (12.2) определяются рядом геометрической прогрессии:
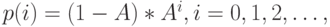 |
( 12.18) |
поскольку 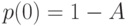 . Вероятность задержки равна:
. Вероятность задержки равна:
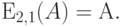
Средняя длина очереди 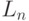 (12.12) и среднее время ожидания для всех вызовов
(12.12) и среднее время ожидания для всех вызовов 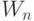 (12.15) :
(12.15) :
 |
( 12.19) |
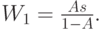 |
( 12.20) |
С помощью уравнений 12.12, 12.14, 12.17 мы можем установить, что увеличение нагрузки из-за большего количества вызовов лучше, чем увеличение нагрузки из-за более длинного времени обслуживания, поскольку увеличение времени обслуживания увеличивает величину всех показателей. Поэтому важно, чтобы времена обслуживания системы не увеличивались в момент перегрузки.
Пример 12.2.2: Среднее время ожидания, когда A -> 0
Заметьте, что если 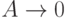 , мы получаем
, мы получаем 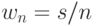 (12.17). Если клиент ожидает (что редко случается, когда
(12.17). Если клиент ожидает (что редко случается, когда 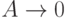 ), то этот клиент будет единственным в очереди. Клиент должен ждать, пока сервер освободится. Это случается в конце экспоненциально распределенного временного интервала со средней величиной
), то этот клиент будет единственным в очереди. Клиент должен ждать, пока сервер освободится. Это случается в конце экспоненциально распределенного временного интервала со средней величиной  . Поэтому
. Поэтому 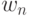 никогда не может быть меньше, чем
никогда не может быть меньше, чем  .
.
Функция увеличения для M/M/n
Предельное увеличение нагрузки, которую может обслуживать система, когда мы дополняем число обслуживающих приборов, может быть выражено несколькими способами. Уменьшение отношения нагрузки канала к полной нагрузке (пропорционально числу всех вызовов от клиентов) определяется как:
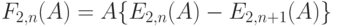 |
( 12.21) |
Уменьшение средней длины очереди (пропорционально нагрузке, которую обслуживают места ожидания) определяется формулой Литла (12.14):
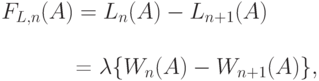 |
( 12.22) |
где 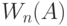 - среднее время ожидания для всех вызовов, когда предложенная нагрузка и число обслуживающих приборов -
- среднее время ожидания для всех вызовов, когда предложенная нагрузка и число обслуживающих приборов -  (12.15). Равенства (12.21) и (12.22) сведены в таблицу в Принципе Мо (Jensen, 1950 [50] ) и могут быть легко рассчитаны с помощью калькулятора или компьютера.
(12.15). Равенства (12.21) и (12.22) сведены в таблицу в Принципе Мо (Jensen, 1950 [50] ) и могут быть легко рассчитаны с помощью калькулятора или компьютера.