|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Полнодоступные системы с потерями
Все эти модели не зависят от распределения времени обслуживания. Модели Энгсета и Паскаля не зависят также и от распределения свободного времени источников. После введения в секции 8.1 мы рассматриваем основную классическую теорию. В секции 8.2 рассмотрим биноминальный случай, где число источников S (абонентов, клиентов, заявителей) ограничено и число каналов я всегда достаточно  . Для этой системы применяются уравнения равновесия, такие же, как и в случае Пуассоновского распределения (секция 7.2). Мы рассматриваем стратегию с явными потерями вызовов ( LCC - Lost-Calls-Cleared).
. Для этой системы применяются уравнения равновесия, такие же, как и в случае Пуассоновского распределения (секция 7.2). Мы рассматриваем стратегию с явными потерями вызовов ( LCC - Lost-Calls-Cleared).
В секции 8.3 пойдет разговор о случае, когда число каналов ограничено так, чтобы оно стало меньше, чем число источников (n < S). Мы можем тогда рассмотреть блокировку и получим усеченное биноминальное распределение, которое также названо Распределением Энгсета.
Вероятность потерь по времени Е определяется формулой Энгсета. В системах с ограниченным числом источников потери по времени, потери по вызовам и потери по нагрузке различаются. Их зависимость определяется теоремой поступления заявок, которая утверждает: "вероятность состояния системы, наблюдаемой клиентом (математическое ожидание по вызовам), равна вероятности состояния системы без этого клиента

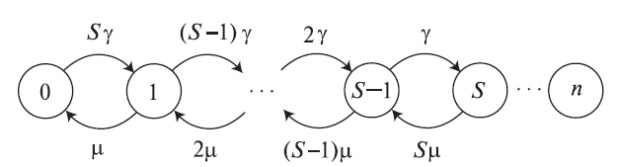
Рис. 8.1. Полнодоступная система с потерями с S источниками, которая генерирует нагрузку на я каналов. Система показана в виде так называемой chicko-граммы. "Клюв" источника символизирует устройство выбора и указывает на каналы (обслуживающие приборы), которые может выбрать источник.
(математическое ожидание по времени)". Формула Энгсета вычисляется с помощью рекурсивной формулы, при числе каналов п, полученной тем же самым способом, как и В-формула Эрланга.
Также получена рекурсивная формула для числа источников S и n, и для п и S вместе. Ее также называют моделью Паскаля, где интенсивность поступления вызовов увеличивается линейно с состоянием системы. Если число каналов ограничено, мы получаем у сеченное Отрицательное Биноминальное распределение (секция 8.7).
Введение
Мы рассматриваем систему, как имеющую ту же самую структуру (полнодоступная группа) и стратегию (потерянный вызов покидает систему без влияния на дальнейшие процессы), как и в Лекции 7. Далее мы предполагаем, что времена обслуживания являются экспоненциально распределенными с интенсивностью  (средняя величина
(средняя величина 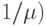 ; процесс нагрузки тогда становится процессом рождения и гибели, специальным марковским процессом, который является математически простым. Обычно мы определяем состояние системы как число занятых каналов. Все процессы, которые рассматриваются в Лекции 7 и 8, не зависят от распределения времени обслуживания, то есть среднее время обслуживания важно только для вероятностей состояния. Распределение самого времени обслуживания не имеет никакого влияния.
; процесс нагрузки тогда становится процессом рождения и гибели, специальным марковским процессом, который является математически простым. Обычно мы определяем состояние системы как число занятых каналов. Все процессы, которые рассматриваются в Лекции 7 и 8, не зависят от распределения времени обслуживания, то есть среднее время обслуживания важно только для вероятностей состояния. Распределение самого времени обслуживания не имеет никакого влияния.
Определение предложенной нагрузки. В секции 2.1 мы определили предложенную нагрузку как нагрузку, которую может обслужить неограниченное число обслуживающих приборов, и это определение используется и для модели Энегсета, и для модели Паскаля. Предложенная нагрузка, таким образом, независима от числа обслуживающих приборов.
Только для стационарных процессов восстановления, таких, как Пуассоновский поток вызовов в случае модели Эрланга, это определение эквивалентно среднему числу попыток вызовов, которые поступают за среднее время обслуживания. В модели Энгсета и Паскаля процессы поступления вызовов - не процессы обновления, так как среднее время интервала зависит от фактического состояния.
Пиковость определяется как отношение между дисперсией и средней величиной вероятностей состояния. Для предложенной нагрузки пиковость рассматривается для бесконечного числа каналов.
Мы рассматриваем следующие процессы поступления вызовов (с первой моделью мы уже имели дело в Лекции 7):
-
Модель Эрланга (Р-Пуассоновская модель)
Процесс поступления вызовов - Пуассоновский процесс с интенсивностью
 . Этот тип нагрузки называется случайная нагрузка или Чистая Случайная Нагрузка первого типа один , РСТ1. Мы рассматриваем два случая:
. Этот тип нагрузки называется случайная нагрузка или Чистая Случайная Нагрузка первого типа один , РСТ1. Мы рассматриваем два случая: -
Модель Энегсета (5-Биноминальная модель):
Имеется ограниченное число источников S. Отдельный источник имеет постоянную интенсивность поступления вызовов (прибытие), когда он свободен. Когда он занят, интенсивность вызовов рана нулю.
Процесс поступления вызовов, таким образом, зависит от состояния. Если i /-тый источник занят, то интенсивность поступления вызовов равна (S-i).
Этот тип нагрузки назван Чистым Случайным Нагрузки типа Два, РСТII. Мы рассматриваем следующие два случая:
- Модель Палъма-Волъстрема (Р-модель Паскаля):
Пусть имеется ограниченное число источников S. Если в данный момент мы имеем i занятых источников, тогда интенсивность прибытия равняется  .
.
Опять мы имеем два случая:
-
 : распределение Паскаля = Отрицательное Биноминальное распределение (секция 8.6). В этом случае пиковость больше, чем единица: Z > 1.
: распределение Паскаля = Отрицательное Биноминальное распределение (секция 8.6). В этом случае пиковость больше, чем единица: Z > 1. -
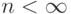 : Усеченное распределение Паскаля (усеченное отрицательное Биноминальное распределение) (секция 8.7).
: Усеченное распределение Паскаля (усеченное отрицательное Биноминальное распределение) (секция 8.7).
Так как Пуассоновский процесс может быть получен при бесконечном числе источников с ограниченной полной интенсивностью поступления вызовов  , модель Эрланга можно рассматривать как специальный случай двух других случаев:
, модель Эрланга можно рассматривать как специальный случай двух других случаев:
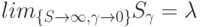
Для любого конечного состояния i мы тогда имеем постоянную интенсивность поступления вызовов:

Третий тип нагрузки упоминается как ВРР-нагрузка (согласно сокращениям, данным выше: Биноминальная, и Пуассоновская, и Паскалевская). Эти модели включают все значения пиковости Z > 0, они могут использоваться для моделирования нагрузки с двумя параметрами: средняя величина и пиковость Z. Для произвольных значений Z число источников S вообще может стать не целым.
Рабочие характеристики: параметры рабочих характеристик для систем с потерями - потери по времени Е, потери по вызовам В, потери по нагрузке С и использование каналов. Среди них потери по нагрузке С - самая важная характеристика. Эти меры получены для каждой из вышеупомянутых моделей.
Биноминальное Распределение (Модель Энгсета)
Мы рассматриваем систему с ограниченным числом источников (абонентов) S. Источник переключается из состояния "свободно" в состояние "занято" и наоборот. Свободный источник в течение временного интервала передает заявки с экспоненциально распределенной интенсивностью  . Источник занят в течение экспоненциально распределенного временного интервала (время обслуживания, время пребывания в системе) с интенсивностью
. Источник занят в течение экспоненциально распределенного временного интервала (время обслуживания, время пребывания в системе) с интенсивностью  (рис.8.2). Этот вид источников называется спорадическими источниками или источники включить /выключить. Такой тип нагрузки называется Чистой Случайной Нагрузкой типа Два (РСТII) или псевдослучайной нагрузкой.
(рис.8.2). Этот вид источников называется спорадическими источниками или источники включить /выключить. Такой тип нагрузки называется Чистой Случайной Нагрузкой типа Два (РСТII) или псевдослучайной нагрузкой.
В этой секции предполагается, что число каналов/пучков каналов я больше или равняется числу источников 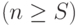 , так, чтобы не было потерь вызовов. Предполагается, что n и S - целые числа, но можно рассматривать и не целые значения чисел (Iversen и Sanders, 2001 [43]).
, так, чтобы не было потерь вызовов. Предполагается, что n и S - целые числа, но можно рассматривать и не целые значения чисел (Iversen и Sanders, 2001 [43]).
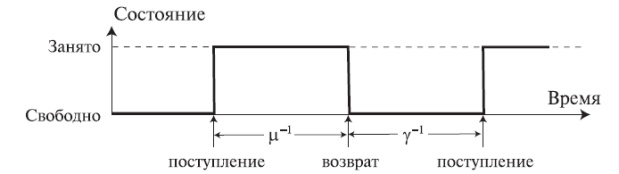
Рис. 8.2. Каждый отдельный источник является либо свободным, либо занятым, и ведет себя независимо от всех других источников.
Уравнения равновесия
Мы интересуемся только вероятностями устойчивых состояний (i). Они пропорциональны времени, которое процесс находится в состоянии [i]. Наши вычисления основаны на диаграмме переходов состояний на рис. 8.3. Мы рассматриваем сечения между соседними состояниями и находим:
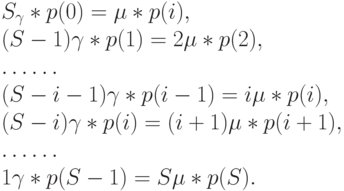 |
( 8.1) |
Число источников S меньше или равно числу каналов  .
.
Все вероятности состояний могут быть выражены через р (0):
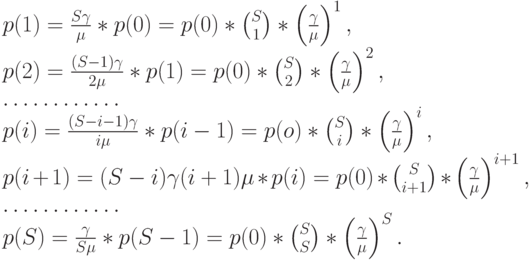
Полная сумма всех вероятностей должна быть равна единице:
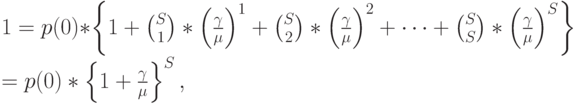 |
( 8.2) |
где мы использовали развернутый бином Ньютона; обозначая 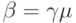 , мы получаем:
, мы получаем:
 |
( 8.3) |
Параметр  - предложенная нагрузка на свободный источник (число попыток вызова в единицу времени для свободного источника - предложенная нагрузка от занятого источника является нулевой), тогда мы находим:
- предложенная нагрузка на свободный источник (число попыток вызова в единицу времени для свободного источника - предложенная нагрузка от занятого источника является нулевой), тогда мы находим:
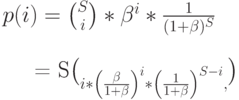
это выражение называется Биноминальным распределением (таблица 6.1). Наконец, мы получаем:
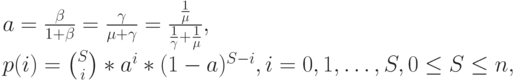 |
( 8.4) |
В том случае, когда попытка вызова от свободного источника никогда не блокируется, параметр а равен обслуженной нагрузке у на один источник (а=у) - он является эквивалентным вероятности того, что источник занят в случайный момент времени. Это также видно из рис.8.2, так как все точки поступления и возврата на осях времени - точки регенерации (точки равновесия). Цикл от начала занятого состояния (поступления) до начала следующего занятого состояния представлен для всей оси времени, и математические ожидания времени получены в среднем по одному циклу. Заметим, что для систем с блокировкой мы имеем  (см. секцию 8.3).
(см. секцию 8.3).
Биноминальное распределение, полученное в (8.4), иногда в теории телетрафика называют распределением Бернулли, но мы этого избегаем, так как в статистике это название используется для распределения с двумя точками.
Формула (8.4) может быть получена с применением элементарных соображений. Все абоненты могут быть разбиты на два класса: свободные и занятые. Существует вероятность того, что произвольный абонент принадлежит классу занятых (у= а) и не зависит от состояния всех других абонентов, так как система не имеет блокировки, и попытки вызова всегда принимаются. Есть всего S абонентов (источников), и вероятность того, что i источников заняты в произвольный момент p(i), определяется Биноминальным распределением (8.4) и таблицей 6.1.
Характеристики Биноминальной нагрузки
Мы суммируем определения параметров, данные выше:
 |
( 8.5) |
 |
( 8.6) |
 |
( 8.7) |
По определению, предложенная нагрузка источника равна обслуженной нагрузке в системе без потерь, где источник свободно переключается между состоянием свободно и занято. Поэтому мы имеем следующее определение предложенной нагрузки:
 |
( 8.8) |
 |
( 8.9) |
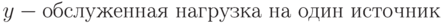 |
( 8.10) |
 |
( 8.11) |
Предложенная нагрузка на свободный источник - понятие, трудное для практического применения, потому что соотношение времени, когда источник является свободным, зависит от потерь. Число вызовов, предлагаемых источником, зависит от числа каналов (обратная связь): высокая перегрузка каналов приводит к увеличению продолжительности пребывания источников вызова в состоянии "свободно". Это, в свою очередь, приводит к увеличению числа попыток вызова.
Потери по времени:
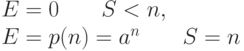 |
( 8.12) |
Обслуженная нагрузка:
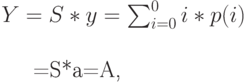 |
( 8.13) |
она является средней величиной Биноминального распределения (8.4). В этом случае без блокировки мы, конечно, имеем а=у и, кроме того, выполняются следующие соотношения. Потери по нагрузке:
 |
( 8.14) |
Число попыток вызовов в единицу времени:
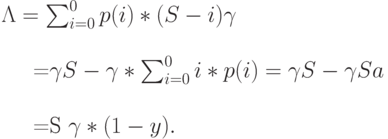
Когда все вызовы приняты, мы получаем: Перегрузка по вызовам
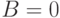 |
( 8.15) |
Нагрузка, обслуживаемая каналом v.
Случайный поиск:
 |
( 8.16) |
Последовательный поиск: это сложное выражение, полученное L.A. Joys (1971 [56]).
Функция увеличения:
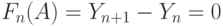 |
( 8.17) |
Пиковость (табл. 6.1):
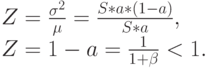 |
( 8.18) |
Мы видим, что пиковость Z нe зависит от числа источников и всегда меньше единицы, что соответствует сглаженной нагрузке.
Продолжительность состояния i экспоненциально распределена со скоростью:
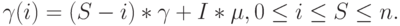 |
( 8.19) |
Конечная исходная нагрузка характеризуется числом источников S и предложенной нагрузкой от одного свободного источника  Альтернативно, на практике мы часто используем предложенную нагрузку и пиковость Z. Мы имеем следующие отношения между этими двумя представлениями:
Альтернативно, на практике мы часто используем предложенную нагрузку и пиковость Z. Мы имеем следующие отношения между этими двумя представлениями:
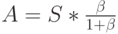 |
( 8.20) |
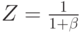 |
( 8.21) |
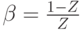 |
( 8.22) |
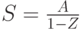 |
( 8.23) |

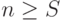 :
: