Алгоритм AES. Режимы выполнения алгоритмов симметричного шифрования. Создание случайных чисел
Создание случайных чисел
Случайные числа играют важную роль при использовании криптографии в различных сетевых приложениях, относящихся к безопасности. Сделаем краткий обзор требований, предъявляемых к случайным числам в приложениях сетевой безопасности, а затем рассмотрим несколько способов создания случайных чисел.
Требования к случайным числам
Большинство алгоритмов сетевой безопасности, основанных на криптографии, использует случайные числа. Например:
- Схемы взаимной аутентификации. В большинстве сценариев аутентификации и распределения ключа для предотвращения атак повтора (replay-атак) используются случайные числа, ко-торые в этом случае называются nonсe (number only once – число, используемое только один раз). Применение действительно случайных чисел в качестве nonce не дает противнику возможности вычислить или угадать nonce.
- Ключ сессии, созданный центром распределения ключей (Key Distribution Center – KDC) или кем-либо из участников.
Двумя основными требованиями к последовательности случайных чисел являются случайность и непредсказуемость.
-
Случайность
Обычно при создании последовательности псевдослучайных чисел предполагается, что данная последовательность чисел должна быть случайной в определенном статистическом смысле. Следующие два критерия используются для доказательства того, что последовательность чисел является случайной:
Однородное распределение: распределение чисел в последовательности должно быть однородным; это означает, что частота появления каждого числа должна быть приблизительно одинаковой.
Независимость: ни одно значение в последовательности не должно зависеть от других.
Хотя существуют тесты, показывающие, что последовательность чисел соответствует некоторому распределению, такому как однородное распределение, теста для "доказательства" независимости нет. Тем не менее, можно подобрать набор тестов для доказательства того, что последовательность является зависимой. Общая стратегия предполагает применение набора таких тестов до тех пор, пока не будет уверенности, что независимость существует.
-
Непредсказуемость
В приложениях, таких как взаимная аутентификация и генерация ключа сессии, нет жесткого требования, чтобы последовательность чисел была статистически случайной, но члены последовательности должны быть непредсказуемы. При действительно случайной последовательности каждое число статистически не зависит от остальных чисел и, следовательно, не-предсказуемо. Однако последовательность случайных чисел на практике должна создаваться некоторым алгоритмом. В этом случае необходимо, чтобы нельзя было предугадать следующие элементы последовательности, зная предыдущие элементы и используемый алгоритм.
Источники случайных чисел
Источники действительно случайных чисел найти трудно. Физические генераторы шумов, такие как детекторы событий ионизирующей радиации, газовые разрядные трубки и имеющий течь конденсатор могут быть такими источниками. Однако эти устройства в приложениях сетевой безопасности имеют ограниченное применение. Проблемы также могут возникнуть, если на эти устройства будут осуществлены атаки. Альтернативным решением является создание набора из большого числа случайных чисел и опубликование его в некоторой книге. Однако такие наборы обеспечивают очень небольшое количество чисел по сравнению с тем количеством, которое требуется приложениям сетевой безопасности. Более того, хотя такие числа действительно обеспечивает статистическую случайность, они предсказуемы, так как противник может получить их копию.
Поэтому для создания случайных чисел приложения используют спе-циальные алгоритмы. Эти алгоритмы детерминированы и, следовательно, создают последовательность чисел, которая не является статистически случайной. Тем не менее, если алгоритм хороший, полученная последовательность будет проходить много тестов на случайность. Такие числа часто называют псевдослучайными числами.
Рассмотрим несколько алгоритмов генерации псевдослучайных чисел.
Генераторы псевдослучайных чисел
В криптографических приложениях целесообразно шифровать полу-чающиеся случайные числа. Чаще всего используется три способа.
-
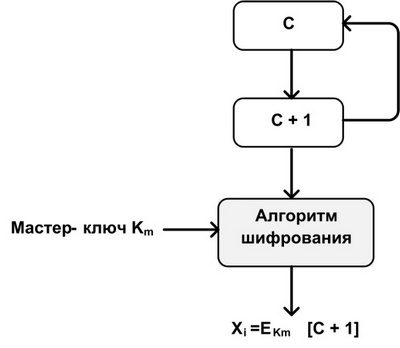
Циклическое шифрование
В данном случае применяется способ создания ключа сессии из мастер-ключа. Счетчик с периодом N используется в качестве входа в шифрующее устройство. Например, в случае использования 56-битного ключа DES может применяться счетчик с периодом 256. После каждого созданного ключа значение счетчика увеличивается на 1. Таким образом, псевдослучайная последовательность, полученная по данной схеме, имеет полный период: каждое выходное значение Х0, Х1,...ХN-1 основано на различных значениях счетчика и, следовательно, Х0 ? X1 ? XN-1. Так как мастер-ключ защищен, то полученное случайное число не зависит от предыдущих случайных чисел.
Для дальнейшего усиления алгоритма вход должен быть выходом пол-нопериодического генератора псевдослучайных чисел, а не простой после-довательностью.
-
Режим Output Feedback DES
Режим OFB DES может применяться для генерации ключа, аналогично тому, как он используется для потокового шифрования. Заметим, что выхо-дом каждой стадии шифрования является 64-битное значение, из которого только левые j битов подаются обратно для шифрования. 64-битные выходы составляют последовательность псевдослучайных чисел с хорошими статистическими свойствами.
-
Генератор псевдослучайных чисел ANSI X9.17
Один из наиболее сильных генераторов псевдослучайных чисел описан в стандарте ANSI X9.17. В число приложений, использующих эту технологию, входят приложения финансовой безопасности и PGP.
Используется алгоритм шифрования тройной DES. Генератор ANSI X9.17 состоит из следующих частей:
Вход: генератор имеет два псевдослучайных входа. Один является 64-битным представлением текущей даты и времени, которые изменяются каждый раз при создании числа. Другой является 64-битным начальным значением; оно инициализируется некоторым произвольным значением и изменяется входе генерации последовательности псевдослучайных чисел.
Ключи: генератор трижды использует алгоритм тройного DES. Все три раза используется одна и та же пара 56-битных ключей, которая должна держаться в секрете и применяться только для генерации псевдослучайного числа.
Выход состоит из 64-битного псевдослучайного числа и 64-битного значения, которое будет использоваться в качестве начального значения при создании следующего числа.
DTi – значение даты и времени создания i-го псевдослучайного числа.
Vi – начальное значение при создании i-го псевдослучайного числа.
Ri – i-ое псевдослучайное число.
Ri – i-ое псевдослучайное число.
![R_i = EDE_K_1_,_K_2 [ EDE_K_1_,_K_2 [ DT_i] \oplus V_i ]\\
V_i_+_1 = EDE_K_1_,_K_2 [ EDE _K_1_,_K_2 [ DT_i] \oplus R_i ]](/sites/default/files/tex_cache/127978293e68d5a7e2898218b512c893.png)
Даже если псевдослучайное число Ri будет скомпрометировано, вычислить Vi+1 из Ri невозможно, и, следовательно, невозможно найти следующее псевдослучайное значение Ri+1.