Алгоритм AES. Режимы выполнения алгоритмов симметричного шифрования. Создание случайных чисел
Понятие состояния, ключ шифрования и число раундов
Различные преобразования выполняются над промежуточным значением блока, называемым состоянием
Состояние можно рассматривать как двумерный массив байтов. Этот массив имеет четыре строки и различное число столбцов, обозначаемое как Nb, равное длине блока, деленной на 32. Ключ также можно рассматривать как двумерный массив с четырьмя строками. Число столбцов ключа шифрования, обозначаемое как Nk, равно длине ключа, деленной на 32.
В некоторых случаях блок шифруемого сообщения рассматривается как одномерный массив четырехбайтных векторов, где значениями каждого вектора являются значения соответствующего столбца. Такие массивы имеют длину 4, 6 или 8 соответственно, и индексы в диапазонах 0…3, 0…5 или 0…7. Четырехбайтные вектора иногда мы будем называть словами.
Если необходимо указать четыре отдельных байта в четырехбайтном векторе, будет использоваться нотация (a, b, c, d), где a, b, c и d являются байтами в позициях 0, 1, 2 и 3, соответственно, в рассматриваемом столбце, векторе или слове.
Входы и выходы Rijndael считаются одномерными массивами из 8 бай-тов, пронумерованными от 0 до 4* Nb – 1. Следовательно, эти блоки имеют длину 16, 24 или 32 байта, и массив индексируется в диапазонах 0 … 15, 0 … 23 или 0 … 31. Ключ считается одномерным массивом 8-битных байтов, пронумерованных от 0 до 4* Nk – 1. Следовательно, эти блоки имеют длину 16, 24 или 32 байта, и массив индексируется в диапазонах 0 … 15, 0 … 23 или 0 … 31.
Входные байты алгоритма отображаются в байты состояния в следующем порядке: А0,0, А1,0, А2,0, А3,0, А0,1, А1,1, А2,1, А3,1, А0,2, … Байты ключа шифрования отображаются в массив в следующем порядке: K0,0, K1,0, K2,0, K3,0, K0,1, K1,1, K2,1, K3,1, … После выполнения операции шифрования выход алгоритма получается из байтов состояния аналогичным образом.
Следовательно, если одномерный индекс байта в блоке есть n, и двухмерный индекс есть (i,j), то мы имеем:

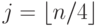

Более того, индекс i является также номером байта в четырехбайтном векторе или слове, j является индексом вектора или слова во вложенном блоке.
Число раундов обозначается Nr и зависит от значений Nb и Nk, что показано в следующей таблице.
Преобразование раунда
Преобразование раунда состоит из четырех различных преобразований. В нотации на псевдо С это можно записать следующим образом:
Round (State, RoundKey)
{
ByteSub (State);
ShiftRow (State);
MixColumn (State);
AddRoundKey (State, RoundKey);
}
Заключительный раунд алгоритма немного отличается и выглядит сле-дующим образом:
FinalRound (State, RoundKey)
{
ByteSub (State);
ShiftRow (State);
AddRoundKey (State, RoundKey);
}
Как мы видим, заключительный раунд эквивалентен остальным, за ис-ключением того, что отсутствует слой MixColumn.
Преобразование ByteSub
Преобразование ByteSub является нелинейной байтовой подстановкой, выполняющейся независимо для каждого байта состояния. Подстановка является обратимой и определена в виде композиции двух преобразований:
Во-первых, выполняется мультипликативная инверсия в GF (28) для определенного выше представления байта в виде полинома 7 степени. ‘00’ отображается сам в себя.
Затем выполняется аффинное (в GF (2)) преобразование, определяемое следующим образом:
Применение описанного S-box ко всем байтам состояния обозначается как
ByteSub (State)
На следующем рисунке показан результат применения преобразования ByteSub к State.
Обратное преобразование ByteSub есть применение байтовой подста-новки в соответствии с инверсной таблицей. Это получается инверсией аффинного отображения и мультипликативной инверсией в GF (28).
Преобразование ShiftRow
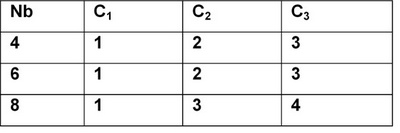
В ShiftRow строки состояния циклически сдвигаются на различные значения. Нулевая строка не сдвигается. Строка 1 сдвигается на С1 байтов, строка 2 на С2 байтов, строка 3 на С3 байтов. Величины С1, С2 и С3 зависят от Nb. Значения приведены в следующей таблице.
Операция сдвига строк на указанные значения обозначается как
ShiftRow (State)
Инверсией для ShiftRow является циклический сдвиг трех нижних строк соответственно на Nb – С1, Nb – С2 и Nb – С3 байт, чтобы байт в позиции j в строке i перемещался в позицию (j + Nb – Ci) mod Nb.
Преобразование MixColumn
В MixColumn столбцы состояния рассматриваются как полиномы в GF(28) и умножаются по модулю х4 + 1 на фиксированный полином:

Данный полином является взаимно простым с х4 + 1 и, следовательно, имеет обратный. Как обсуждалось, это может быть записано в виде умножения матрицы.
Пусть b(x) = c(x) /otimes a(x)
Применение данной операции ко всем столбцам состояния обозначает-ся как
MixColumn (State)
Инверсия MixColumn является преобразованием, аналогичным MixColumn. Каждый столбец преобразуется умножением его на полином d(x), определяемый следующим образом:

В результате получаем

Сложение с ключом раунда
Выполняется операция побитового XOR ключа раунда с текущим состоянием. Длина ключа раунда равна длине блока Nb. Данное преобразование обозначается как
AddRoundKey (State, RoundKey)
AddRoundKey является инверсией самого себя.
Создание ключей раунда
Ключи раунда получаются из ключа шифрования с помощью преобразования, состоящего из двух компонентов: расширение ключа и выбор ключа раунда. Основные свойства, которыми обладают ключи раунда:
- Общее число битов для ключей раундов равно длине блока, умноженной на количество раундов плюс 1. Например, для длины блока 128 бит и 10 раундов необходимо 1408 битов для ключей раундов.
- Сначала выполняется расширение ключа.
- Ключи раунда получаются из этого расширенного ключа следующим способом: первый ключ раунда состоит из первых Nb слов, второй состоит из следующих Nb слов и т.д.
Расширение ключа
Расширенный ключ является линейным массивом четырехбайтных слов и обозначается как W [Nb * (Nr + 1)]. Первые Nk слов состоят из ключа шифрования. Остальные слова определяются рекурсивно. Функция расширения ключа зависит от значения Nk: существует версия функции для Nk, равным или меньшим 6, и версия для Nk больше 6.
Для Nk ? 6 мы имеем:
KeyExpansion (byte Key [4*Nk] word W[Nb * (Nr + 1)])
{
for (i = 0; i < Nk; i++)
W[i] =(Key [4*i], Key [4*i+1], Key [4*i+2], Key [4*i+3]);
for (i = Nk; i < Nb * (Nr + 1); i++) {
temp = W [i – 1];
if (i % Nk == 0)
temp = SubByte (RotByte (temp)) ^ Rcon [i / Nk];
W [i] = W [i- Nk] ^ temp;
}
}
В данном случае SubByte (W) является функцией, которая возвращает четырехбайтное слово, в котором каждый байт является результатом применения S-box Rijndael к байту в соответствующей позиции во входном слове. Функция RotByte(W) возвращает слово, в котором байты циклически переставлены таким образом, что для входного слова (a, b, c, d) создается выходное слово (b, c, d, a).
Можно заметить, что первые Nk слов заполняются ключом шифрования. Каждое следующее слово W[i] равно XOR предыдущего слова W[i-1] и позиций слова Nk до W[i – Nk]. Для слов в позициях, которые кратны Nk, сначала применяется преобразование XOR к W[i-1] и константой раунда. Данное преобразование состоит из циклического сдвига байтов в слове (RotByte), после чего выполняется табличная подстановка для всех четырех байтов в слове (SubByte).
Для Nk > 6 мы имеем:
KeyExpansion (byte Key [4*Nk] word W [Nb* (Nr+1)])
{
for (i=0; i < Nk; i++)
W[i]= (key [4*i], key [4*i+1], key [4*i+2], key [4*i+3]);
for (i = Nk; i < Nb * (Nr + 1); i++) {
temp = W [i-1];
if (i % Nk == 0)
temp = SubByte (RotByte (temp)) ^ Rcon [i / Nk];
else if (i % Nk == 4)
temp = SubByte (temp);
W[i] = W[i – Nk] ^ temp;
}
}
Отличие для Nk ? 6 состоит в том, что для i-4, кратных Nk, SubByte применяется для W[i-1] перед выполнением XOR.
Константы раунда не зависят от Nk и определяются следующим образом:
Rcon [i] = (RC [i], ‘00’, ‘00’, ‘00’)
RC [i] являются элементами в GF (28) со значением x(i-1) таким, что:
RC [1] = 1 (т.е. ‘01’) RC [i] = x (т.е. ‘02’) • (RC [i-1]) = x(i-1)
Ключ раунда i получается из слов буфера ключа раунда W [Nb * i] до W [Nb * (i+1)].
Преимущества алгоритма
Преимущества, относящиеся к аспектам реализации:
- Rijndael может выполняться быстрее, чем обычный блочный алгоритм шифрования. Выполнена оптимизация размера таблицы и скорости выполнения.
- Rijndael можно реализовать в смарткарте в виде кода, используя небольшой RAM и имея небольшое число циклов. Выполнена оптимизация размера ROM и скорости выполнения.
- Преобразование раунда допускает параллельное выполнение, что является важным преимуществом для будущих процессоров и специализированной аппаратуры.
- Алгоритм шифрования не использует арифметические операции, поэтому тип архитектуры процессора не имеет значения.
Простота разработки:
- Алгоритм шифрования полностью "само определяемый". Он не использует других криптографических компонентов, S-box, взятых из хорошо известных алгоритмов, битов, полученных из специальных таблиц, чисел типа p и тому подобных уловок.
- Алгоритм не основывает свою безопасность или часть ее на неясностях или плохо понимаемых итерациях арифметических операций.
- Компактность алгоритма не дает возможности спрятать люки.
Переменная длина блока:
- Длины блоков от 192 до 256 бит позволяют создавать хэш-функции без коллизий, использующие Rijndael в качестве функции сжатия. Длина блока 128 бит сегодня считается для этой цели недостаточной.
Расширения:
- Определение алгоритма позволяет специфицировать варианты длины блока и длины ключа в диапазоне от 128 до 256 бит с шагов в 32 бита.
- Хотя число раундов Rijndael для AES фиксировано, в случае возникновения проблем с безопасностью алгtоритм можно модифицировать, сделав число раундов параметром алгоритма.
Расширения алгоритма
Алгоритм может быть модифицирован для использования с другой длиной блока и другой длиной ключа шифрования.
Алгоритм вычисления подключей поддерживает вычисление ключей, длина которых кратна 4 байтам. Единственный параметр, который необходимо учитывать при определении длины ключа, является количество раундов алгоритма.
Структура алгоритма допускает длину блока, кратную 4 байтам. Минимальная длина блока должна быть 16 байтов. Увеличение длины ключа, ByteSub и MixColumn преобразования не зависят от длины блока. Единственным преобразованием, которое зависит от длины блока, является ShiftRow. Для каждой длины блока должны быть определены соответствующие константы С1, С2, С3.
Можно определить расширение Rijndael, которое также поддерживает длины блока и ключа между 128 и 256 битами с шагом 32 бита. Число раундов определяется следующим образом:

Данное выражение задает правило определения количества раундов для альтернативных значений длины блока и длины ключа.
Соответствующие значения С1, С2 и С3 указаны в следующей таблице.