Алгоритм AES. Режимы выполнения алгоритмов симметричного шифрования. Создание случайных чисел
Умножение на х
При умножении b(x)на полином х получаем:

Для вычисления x • b(x) необходимо результат взять по модулю m(x). Если b7 = 0, то результатом является исходный полином, для которого выполнен сдвиг на 1 бит влево. Если b7 = 1, то кроме сдвига влево на 1 бит следует выполнить операцию XOR с m(x). Следовательно, умножение на х на уровне байта есть левый сдвиг и в зависимости от значения b7 побитовый XOR c ‘1B’. Данная операция обозначается как xtime (b).
Использование данной операции позволяет более быстро выполнить умножение двух байтов.
Полиномы с коэффициентами из GF (2^8)
Полиномы могут быть определены с коэффициентами из GF (28). В этом случае четырехбайтный вектор соответствует полиному степени 4.
Операцию сложения можно ввести как XOR соответствующих коэффи-циентов.
Умножение вводится более сложным способом. Предположим, что мы имеем два полинома в GF (28).

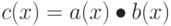 определяется следующим образом:
определяется следующим образом:

Ясно, что в таком виде с(х)не может быть представлен четырехбайтным вектором. Если понизить с(х) по модулю полинома 4-й степени, то результат будет полиномом не выше 3 степени. В Rijndael для этого используется полином
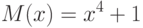
В этом случае
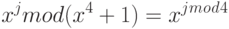
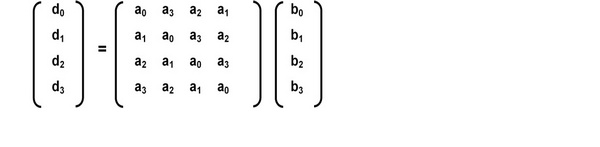
Остаток от деления а(х)•b(x)на M(x)обозначим d(x) = a(x)⊗ b(x).
Коэффициенты d(x)равны:
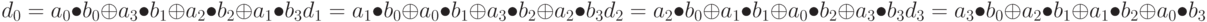
Операция, состоящая из умножения на фиксированный полином а(х), может быть записана как умножение на матрицу, где матрица является циркулярной. Мы имеем
Заметим, что х4+ 1 не является несократимым полиномом в GF (28), следовательно, умножение на фиксированный полином необязательно обратимо. В алгоритме Rijndael выбран фиксированный полином, который имеет обратный.
Умножение на х
При умножении b(x)на полином х имеем:
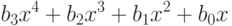
x × b(x)получается понижением полученного результата по модулю х4+1. Получаем

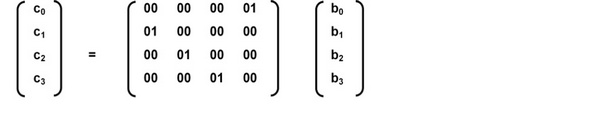
Умножение на х эквивалентно умножению на матрицу, как описано выше, со всеми ai=‘00’ за исключением а1 = ‘01’.
Имеем:
Следовательно, умножение на х соответствует циклическому сдвигу байтов внутри вектора.
Обоснование разработки
В основу разработки алгоритма были положены следующие три критерия:
- Противодействие всем известным атакам;
- Достаточно хорошая скорость выполнения и компактность ко-да для широкого круга платформ;
- Простота разработки.
В большинстве алгоритмов шифрования преобразование каждого ра-унда имеет структуру сети Фейштеля. В этом случае обычно часть битов в каждом промежуточном состоянии просто перемещается без изменения в другую половину. Преобразование раунда алгоритма Rijndael не имеет структуру сети Фейштеля. Вместо этого преобразование каждого раунда состоит из четырех различных преобразований, называемых слоями.
Каждый слой разрабатывался с учетом противодействия линейному и дифференциальному криптоанализу. В основу каждого слоя положена своя функция:
- Нелинейное преобразование состоит в применении S-box, которые улучшают нелинейные свойства в наихудшем случае.
- Слой линейного перемешивания строк гарантирует высокую степень диффузии для нескольких раундов.
- Слой линейного перемешивания столбцов также гарантирует высокую степень диффузии для нескольких раундов.
- Слой сложения с ключом состоит из простого XOR текущего состояния с ключом раунда.
Перед первым раундом применяется дополнительное забеливание с ис-пользованием ключа. Причина того, что в забеливании используется ключ, состоит в следующем. Любой слой после последнего или до первого добавления ключа может быть просто снят без знания ключа и тем самым не добавляет безопасности в алгоритм (например, начальная и конечная перестановки в DES).
Для того чтобы сделать структуру алгоритма более простой, слой ли-нейного перемешивания последнего раунда отличается от слоя перемешивания других раундов. Можно показать, что это в любом случае не повышает и не понижает безопасность.
Описание алгоритма
Rijndael является блочным алгоритмом шифрования с переменной длиной блока и переменной длиной ключа. Длина блока и длина ключа могут быть независимо друг от друга установлены в 128, 192 или 256 бит.