Концептуальное проектирование систем в Anylogic 7 и GPSS World
[+]
Опубликован: 07.11.2014 | Доступ: свободный | Студентов: 442 / 37 | Длительность: 15:17:00
ISBN: 978-5-9556-0161-8
Тема: САПР
Специальности: Программист, Системный архитектор, Архитектор программного обеспечения, Разработчик аппаратуры
Лекция 10:

Модель обработки документов в организации
A
|
версия для печати
< Лекция 9 || Лекция 10: 123 || Дополнительный материал 1 >
Ключевые слова: группа, среднее время, поток, граф, отношение, вероятность, simulation, модельное время, программа

Постановка задачи

Для приёма и обработки документов в организации назначена группа в составе трёх сотрудников. Ожидаемая интенсивность потока документов - 15 документов в час. Среднее время обработки одного документа одним сотрудником - 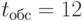t_{обс} = 12 мин. Каждый сотрудник может принимать документы из любой организации. Освободившийся сотрудник обрабатывает последний из поступивших документов. Поступающие документы должны обрабатываться с вероятностью не менее 0,95.

Определить, достаточно ли назначенной группы из трёх сотрудников для выполнения поставленной задачи.

Аналитическое решение задачи

Группа сотрудников работает как СМО, состоящая из трёх каналов, с отказами, без очереди. Поток документов с интенсивностью \lambda =15\frac{1}{час} можно считать простейшим, так как он суммарный от нескольких организаций. Интенсивность обслуживания \mu = \frac{1}{t_{обс}} = \frac{60}{12} = 5\frac{1}{час}. Закон распределения неизвестен, но это несущественно, так как показано, что для систем с отказами он может быть произвольным. Граф состояний СМО - это схема "гибели и размножения". Для неё имеются готовые выражения для предельных вероятностей состояний системы:

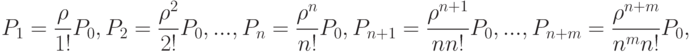
P_1=\frac{\rho }{1!}P_0, P_2=\frac{\rho^2 }{2!}P_0, ..., P_n=\frac{\rho^n }{n!}P_0, P_{n+1}=\frac{\rho^{n+1}}{nn!}P_0, ...,P_{n+m}=\frac{\rho^{n+m}}{n^mn!}P_0,
P_0=\left ( 1+\frac{\rho }{1!}+...+\frac{\rho^n }{n!}+\frac{\rho^{n+1}}{nn!}+\frac{\rho^{n+2}}{n^2n!}+...+\frac{\rho^{n+m}}{n^mn!} \right )^{-1}.

Отношение \rho =\lambda /\mu называют приведенной интенсивностью потока документов (заявок). Физический смысл её следующий: величина \rho представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.

В задаче \rho =\frac{\lambda}{\mu} = \frac{15}{5}=3.

В рассматриваемой СМО отказ наступает при занятости всех трёх каналов, то есть при 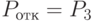P_{отк} = P_3. Тогда:

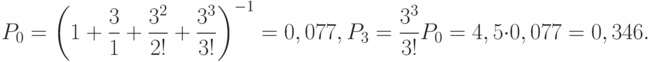
P_0=\left ( 1+\frac{3 }{1}+\frac{3^2}{2!}+\frac{3^3}{3!} \right )^{-1} = 0,077, P_3=\frac{3^3}{3!}P_0=4,5 \cdot 0,077=0,346.

Так как вероятность отказа в обработке документов составляет более 0,34 (0,346), то необходимо увеличить количество сотрудников группы. Увеличим состав группы в два раза, то есть СМО будет иметь теперь шесть каналов, и рассчитаем P_{отк}:

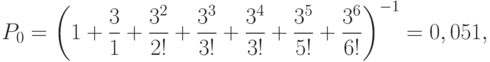
P_0=\left ( 1+\frac{3 }{1}+\frac{3^2}{2!}+\frac{3^3}{3!} +\frac{3^4}{3!} +\frac{3^5}{5!} +\frac{3^6}{6!} \right )^{-1} = 0,051,
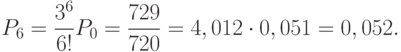
P_6=\frac{3^6}{6!}P_0= \frac{729}{720} = 4,012 \cdot 0,051=0,052.

Теперь P_{обс} = 1-P_{отк} \approx 0,95.

Таким образом, только группа из шести сотрудников сможет обрабатывать поступающие документы с вероятностью 0,95.

Дальше >>
< Лекция 9 || Лекция 10: 123 || Дополнительный материал 1 >

Вопросы и ответы

вопросов: 2
Игорь Маникин
Игорь Маникин

Коллеги, спасибо за очень информативный и полезный курс. Прошёл три лекции. Столкнулся с проблемой, что обе модели не могут закончить расчёт по причине ограничения бесплатной версии "создано максимально допустимое число динамически создаваемых агентов (50000)". По скриншотам Лекции 2 видно, что да, модель создает гораздо больше 50000 агентов. В принципе, мне то и диплом не особо нужен. Но хотелось бы выполнить практические работы. Нет ли возможности откорректировать эту проблему? Или может я чего не так делаю?

Еще раз спасибо за прекрасный курс!

ответить
Артём Нагайцев
Артём Нагайцев

Выдает ошибку "entity cannot be resolved to a variable" при попытке запуска. В чем может быть причина? Ошибка в строках

entity.time_vxod=time(); 

time_obrabotki.add(time()-entity.time_vxod); 

ответить