|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Классические шифры
6.6 Преобразование сдвига
См. [4])
Для ускорения зашифрования и расшифрования удобно иметь относительно простое правило реализации такой перестановки. Один из способов-рассматривать множество целых чисел  и использовать на нем операции сложения и умножения по модулю
и использовать на нем операции сложения и умножения по модулю  .
.
Итак, пусть используется  -буквенный алфавит с числовыми эквивалентами
-буквенный алфавит с числовыми эквивалентами 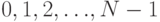 . Пусть
. Пусть  - фиксированное целое число. Преобразованием сдвига будем называть функцию
- фиксированное целое число. Преобразованием сдвига будем называть функцию  , определенную правилом
, определенную правилом 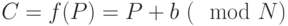 . Случай
. Случай  - это шифрсистема, изобретенная Юлием Цезарем. Для расшифрования элемента шифртекста
- это шифрсистема, изобретенная Юлием Цезарем. Для расшифрования элемента шифртекста 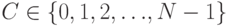 надо будет просто вычислить
надо будет просто вычислить  . Параметр
. Параметр  является ключом зашифрования.
является ключом зашифрования.
Пример 6.8 Предположим, что "FQOCUDEM", которое , как нам известно, зашифровано с использованием преобразования сдвига на буквах 26-буквенного алфавита. Нам надо найти  для успешного "взлома" шифра. Сделать это можно при помощи частотного анализа. Он работает следующим образом. Предположим, что нами перехвачен длинный отрезок шифртекста, скажем, несколько сотен букв. Мы знаем, что "E" - наиболее часто встречающаяся буква английского языка. Поэтому разумно предположить, что наиболее часто встречающаяся в шифртексте буква является результатом зашифрования буквы "E". Пусть чаще других в шифртексте встречается буква "U". Это значит, что сдвиг преобразует "E"=4 в "U"=20, то есть
для успешного "взлома" шифра. Сделать это можно при помощи частотного анализа. Он работает следующим образом. Предположим, что нами перехвачен длинный отрезок шифртекста, скажем, несколько сотен букв. Мы знаем, что "E" - наиболее часто встречающаяся буква английского языка. Поэтому разумно предположить, что наиболее часто встречающаяся в шифртексте буква является результатом зашифрования буквы "E". Пусть чаще других в шифртексте встречается буква "U". Это значит, что сдвиг преобразует "E"=4 в "U"=20, то есть 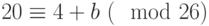 , так что
, так что  . Осталось вычесть 16 (по модулю 26) из числовых эквивалентов "FQOCUDEM":
. Осталось вычесть 16 (по модулю 26) из числовых эквивалентов "FQOCUDEM":
"FQOCUDEM"=5, 16, 14, 2, 20, 3, 4, 12  15, 0, 24, 12, 4, 13, 14, 22="PAYMENOW".
15, 0, 24, 12, 4, 13, 14, 22="PAYMENOW".
Если шифрование применяется к буквам 32-буквенного алфавита, то для  имеется всего 32 возможности, можно просто попробовать их все. И, скорее всего, лишь одному из значений
имеется всего 32 возможности, можно просто попробовать их все. И, скорее всего, лишь одному из значений  будет соответствовать осмысленное сообщение, такое
будет соответствовать осмысленное сообщение, такое  и есть ключ зашифрования.
и есть ключ зашифрования.
Значит, этот тип криптосистем слишком прост, чтобы быть хорошим. Вскрыть его очень легко. Его можно усовершенствовать, используя более широкий класс преобразований, называемых аффинными отображениями: 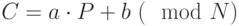 , где
, где  и
и  -фиксированные целые числа(вместе они образуют ключ зашифрования).
-фиксированные целые числа(вместе они образуют ключ зашифрования).
Чтобы расшифровать сообщение, зашифрованное применением аффинного отображения, нужно просто выразить  через
через  , где
, где  есть обратное к
есть обратное к  по модулю
по модулю  число, а
число, а  равно
равно  . Конечно, это возможно лишь при условии
. Конечно, это возможно лишь при условии 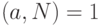 . В противном случае нельзя выразить
. В противном случае нельзя выразить  через
через  : если
: если  , то одной букве шифртекста соответствует несколько букв открытого текста, поэтому нельзя однозначно восстановить открытый текст по зашифрованному. По определению, такое преобразование не является шифрующим, так как последнее обязано быть взаимно однозначным, то есть открытый текст должен определяться шифртекстом однозначно.
, то одной букве шифртекста соответствует несколько букв открытого текста, поэтому нельзя однозначно восстановить открытый текст по зашифрованному. По определению, такое преобразование не является шифрующим, так как последнее обязано быть взаимно однозначным, то есть открытый текст должен определяться шифртекстом однозначно.
Итак, аффинная криптосистема над  -буквенным алфавитом с параметрами
-буквенным алфавитом с параметрами  и
и  задается правилами
задается правилами

где  ,
,  .
.
Как частный случай аффинной криптосистемы при 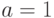 получаем преобразование сдвига. В другом частном случае при
получаем преобразование сдвига. В другом частном случае при 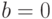 получаем
получаем  ,
, 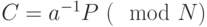 . Такое преобразование называется линейным. Оно отображает сумму в сумму, т. е. если
. Такое преобразование называется линейным. Оно отображает сумму в сумму, т. е. если  при шифровании переходит в
при шифровании переходит в  , а
, а 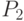 - в
- в  , то
, то  переходит в
переходит в  (сложение, конечно, производится по модулю
(сложение, конечно, производится по модулю  ).
).
Пусть теперь нам известно, что перехваченное сообщение зашифровано применением аффинного отображения букв - буквенного алфавита. Мы хотим определить ключ  ,
,  , чтобы прочитать это сообщение. Для этого нужно знать, как зашифровываются какие-нибудь две буквы.
, чтобы прочитать это сообщение. Для этого нужно знать, как зашифровываются какие-нибудь две буквы.
Используется русский алфавит из 31 буквы: буквы Е и Ё не различаются, буквы И и Й не различаются. Каждой букве такого алфавита поставлено в соответствие число: А соответствует 0, Б-1, В-2,…., Ю-29, Я-30. Известен алгоритм зашифрования: номер буквы открытого текста умножается на число а, к результату прибавляется число b, находится остаток от деления полученного числа на 31. Этот остаток определяет номер буквы в шифрованном тексте. Пробелы и знаки препинания сохранены. Ключом является пара чисел (a, b). Итак, алгоритм известен, ключ Вам неизвестен. При зашифровывании противник не учел особенности русского языка, которые позволят Вам и без знания ключа расшифровать текст. Шифрованный текст:
ВЯТЖХШИАВБ-АНЯЯЖЬГМ, НН ЯИЕЖ ЫИЦВЦИГМ.
Решение. Слову из двух одинаковых букв НН может соответствовать в открытом тексте только слово ЕЁ (напомним, Е и Ё при шифровании не различались). Итак, при расшифровывании нужно Н заменить на Е (Ё).
И у нас есть информация о ключе зашифрования:  .
.
Обратим внимание на третью и четвертую буквы второго слова. Заметим, что наиболее вероятной буквой после Е является Н, биграмма ЕН встречается в русских осмысленных текстах примерно в два раза чаще, чем следующие по частоте биграммы с буквой Е: ЕР, ЕC, ЕЛ . С учетом удвоения буквы тем более вероятно, что символу Я шифрованного текста соответствует буква Н открытого текста.
Конечно, исследуемый текст может оказаться особенным, исключительным. И наша гипотеза может оказаться неверной. В таком случае мы придем к противоречию, к неосмысленному тексту, и нам придется вернуться к началу задачи и проверять другие гипотезы. Однако мы начнем с проверки наиболее вероятной гипотезы: Н Я. На языке сравнений наша гипотеза записывается так:
Я. На языке сравнений наша гипотеза записывается так:  .
.
Вычитая из второго сравнения первое, получаем:  . Из этого сравнения найдем a. Воспользуемся расширенным алгоритмом Евклида. Имеем:
. Из этого сравнения найдем a. Воспользуемся расширенным алгоритмом Евклида. Имеем:

Из последнего равенства:  , из первого равенства
, из первого равенства  , и
, и  . Следовательно,
. Следовательно,  , и
, и  . Теперь
. Теперь 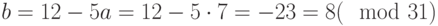 .
.
Мы нашли ключ шифрования. Чтобы расшифровать сообщение, зашифрованное применением отображения  , нужно выразить
, нужно выразить  через
через  , где
, где  есть обратное к
есть обратное к  по модулю 31 число, а
по модулю 31 число, а 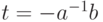 . Так как число 31 простое, то
. Так как число 31 простое, то  и
и  находятся также с помощью расширенного алгоритма Евклида:
находятся также с помощью расширенного алгоритма Евклида:  .
.
Теперь мы можем проводить расшифрование. Букве И соответствует номер 8, и  , так что букве И в шифртексте соответствует буква А в открытом тексте. Подведем итог предыдущим рассуждениям. Символы шифртекста запишем строчными буквами, а уже найденные буквы открытого текста – прописными. Мы имеем:
, так что букве И в шифртексте соответствует буква А в открытом тексте. Подведем итог предыдущим рассуждениям. Символы шифртекста запишем строчными буквами, а уже найденные буквы открытого текста – прописными. Мы имеем:
вНтжхшАавб-аЕННжьгм, ЕЕ НАеж ыАцвцАгм.
Продолжим вычисления. Буква е имеет номер 5, и  , а 4 - это номер буквы Д. Буква ж имеет номер 6,
, а 4 - это номер буквы Д. Буква ж имеет номер 6,  , а это номер буквы О. И мы знаем третье слово полностью: НАДО. Вычисляем букву открытого текста, зашифрованную символом ц: это Щ. Запишем результаты:
, а это номер буквы О. И мы знаем третье слово полностью: НАДО. Вычисляем букву открытого текста, зашифрованную символом ц: это Щ. Запишем результаты:
вНтОхшАавб-аЕННОьгм, ЕЕ НАДО ыАЩвЩАгм.
Тактически правильно будет найти буквы открытого текста, зашифрованные символами г и м. Вычисления дают: г Т,м
Т,м Ь. И мы можем "проявить" еще часть текста:
Ь. И мы можем "проявить" еще часть текста:
вНтОхшАавб-аЕННОьТЬ, ЕЕ НАДО ыАЩвЩАТЬ.
Теперь уже последнее слово легко и угадать. Но все же вычислим еще две буквы. Действительно, ы З,в
З,в И, последнее слово ЗАЩИЩАТЬ. Кроме того, мы узнали еще часть первого слова. Итог этого этапа:
И, последнее слово ЗАЩИЩАТЬ. Кроме того, мы узнали еще часть первого слова. Итог этого этапа:
ИНтОхшАаИб-аЕННОьТЬ, ЕЕ НАДО ЗАЩИЩАТЬ.
Далее, а Ц,ь
Ц,ь С, что позволяет записать второе слово: ЦЕННОСТЬ. Легко вычислить и остальные буквы.
С, что позволяет записать второе слово: ЦЕННОСТЬ. Легко вычислить и остальные буквы.
Ответ: ИНФОРМАЦИЯ-ЦЕННОСТЬ, ЕЕ НАДО ЗАЩИЩАТЬ.
