|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Классические шифры
6.11 Аутентификация
Наряду с конфиденциальностью не менее важной задачей является аутентификация.
Аутентификация - проверка принадлежности субъекту доступа предъявленного им идентификатора; подтверждение подлинности. Иными словами, это процедура определения того, действительно ли пользователь или иной субъект передачи информации (приемопередающее оборудование, узел локальной сети и т. д.) по каналу связи является тем, за кого он себя выдает.
На сегодняшний день механизмы аутентификации широко применяются практически во всех компьютерных системах хранения, передачи и обработки информации, прежде всего, для обеспечения работы систем разграничения доступа и авторизации пользователей системы.
Все механизмы аутентификации основаны на предъявлении пользователем системе специальной информации, на основании которой модуль аутентификации выносит решение о том, считать ли данного пользователя легитимным или признать, что произошла попытка (возможно, неумышленная) подмены пользователя.
Базовая классификация типов систем аутентификации основывается на различии видов информации, используемой в качестве аутентификационной:
- Последовательность информационных символов, которую пользователь предъявляет системе для успешного прохождения аутентификации. Простейший пример - парольная аутентификация на ПЭВМ, для которой пользователю достаточно ввести в систему свой идентификатор и пароль.
- Уникальное содержимое или характеристики предмета. В этом качестве могут выступать, как правило, любые внешние носители информации: смарт-карты, электронные таблетки iButton, USB-токены и т. д. Реже для удаленной аутентификации узла сети могут использоваться уникальные данные о его аппаратном обеспечении.
- Биометрическая информация человека, которая неотъемлема от него и уникальна для каждого индивида. Это может быть отпечаток пальца, рисунок радужной оболочки глаза, форма лица, параметры голоса и т. д.
Используются также комбинированные схемы, основанные на нескольких видах информации, передаваемой системе аутентификации. Типичный пример: аутентификационная информация пользователя для входа в программную систему хранится на смарт-карте, для доступа к которой нужно ввести пароль (PIN-код). Такая аутентификация называется двухфакторной. Намного реже встречаются системы с трехфакторной аутентификацией.
В ряде случаев требуется и взаимная аутентификация - когда оба участника информационного обмена проверяют подлинность идентификаторов друг друга. Например, перед передачей удаленному серверу каких-либо данных пользователь должен убедиться, что это именно тот сервер, который ему необходим.
Помимо этого, существует естественное деление механизмов аутентификации на локальную (в рамках локализованной информационной системы) и удаленную (при передаче информации по каналу связи).
В случае удаленной аутентификации существует проблема передачи аутентификационной информации по недоверенным(ненадежным) каналам связи, так как возникает угроза перехвата аутентификационной информации злоумышленником(противником) с целью дальнейшего использования для атаки на систему защиты.
Рассмотрим несколько задач, моделирующих в упрощенном виде реальную работу системы парольной аутентификации в средствах защиты информации от несанкционированного доступа.
Пример 6.22 (см. [8]) Разделение секрета. Сейф с документами открывается, если набрано секретное число  . Для разделения секрета используется многочлен
. Для разделения секрета используется многочлен 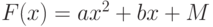 , где a, b - целые числа. Каждый из трех членов комиссии получил свою долю секрета. Именно: первый знает, что
, где a, b - целые числа. Каждый из трех членов комиссии получил свою долю секрета. Именно: первый знает, что  делится на 13 с остатком 3, второй знает:
делится на 13 с остатком 3, второй знает:  делится на 13 с остатком 7, третий знает:
делится на 13 с остатком 7, третий знает:  делится на 13 с остатком 5.
делится на 13 с остатком 5.
Докажите, что объединив свои знания, эти трое смогут открыть сейф (и найдите число  ), а любые двое из них не смогут (числа
), а любые двое из них не смогут (числа  и
и  члены комиссии не знают).
члены комиссии не знают).
Решение. Нужно найти  из условий:
из условий:
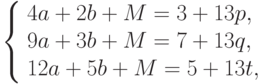
где  ,
,  ,
,  - некоторые целые числа.
- некоторые целые числа.
Складывая первое равенство со вторым, и вычитая из их суммы третье, получим:  , где
, где 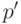 - некоторое целое. Вычитая первое из второго, получим
- некоторое целое. Вычитая первое из второго, получим  .
.
Теперь подставим  ,
,  в первое уравнение. Получим
в первое уравнение. Получим  ,
,  - целое число. Так как каждое число заменяется его остатком от деления на 13, то
- целое число. Так как каждое число заменяется его остатком от деления на 13, то 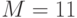 .
.
Поскольку  ,
,  ,
,  - неизвестны, то любые двое, объединившись, получат систему из двух уравнений относительно трех неизвестных.
- неизвестны, то любые двое, объединившись, получат систему из двух уравнений относительно трех неизвестных.
Пример 6.23 (Журнал "Квант") Семизначный код, состоящий из семи различных цифр, назовём хорошим. Известно, что сейф откроется, если введён хороший код и на каком-нибудь месте цифра кода совпала с соответствующей цифрой пароля. За какое наименьшее количество попыток можно с гарантией открыть сейф?
Приведём пример, в котором сейф с гарантией открывается за 6 попыток:
Среди первых 6 цифр пароля есть цифра от 1 до 6. Поскольку мы каждую из 6 цифр по разу набрали на каждом из первых 6 мест, значит, в одном из случаев она совпадает с соответствующей цифрой пароля.
Теперь докажем, что пяти попыток недостаточно. Пусть сделано пять попыток. Обозначим через  множество цифр, которые не набирались в качестве первой цифры в этих попытках. Аналогично определим множества
множество цифр, которые не набирались в качестве первой цифры в этих попытках. Аналогично определим множества  . Так как всего было 5 попыток, то
. Так как всего было 5 попыток, то  (здесь через
(здесь через  обозначаем количество элементов во множестве
обозначаем количество элементов во множестве  ). Так как каждая из цифр
). Так как каждая из цифр  набирались не более одного раза в каждой попытке, то она содержится не менее чем в двух из семи множеств
набирались не более одного раза в каждой попытке, то она содержится не менее чем в двух из семи множеств  . Покажем, что найдётся пароль
. Покажем, что найдётся пароль  , где
, где  - цифра из
- цифра из  ; это и будет означать, что в случае такого пароля сейф не откроется.
; это и будет означать, что в случае такого пароля сейф не откроется.
1 случай. Пусть в двух из множеств  не менее семи цифр, скажем
не менее семи цифр, скажем  ,
,  . Тогда можно выбрать в
. Тогда можно выбрать в  любую цифру
любую цифру  , в
, в  - цифру
- цифру  , отличную от
, отличную от  , и т. д., в
, и т. д., в  - цифру
- цифру  , отличную от
, отличную от 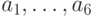 .
.
2 случай. Пусть хотя бы в шести из множеств  не более 6 цифр. Тогда найдётся цифра
не более 6 цифр. Тогда найдётся цифра  , которая не принадлежит двум из этих подмножеств, скажем
, которая не принадлежит двум из этих подмножеств, скажем  не принадлежит
не принадлежит 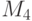 и
и  . Также выберем ещё одну цифру
. Также выберем ещё одну цифру 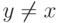 , не принадлежащую
, не принадлежащую  . Цифра
. Цифра  принадлежит хотя бы одному подмножеству
принадлежит хотя бы одному подмножеству  ,
,  , скажем
, скажем  . Цифра
. Цифра  принадлежит хотя бы одному подмножеству
принадлежит хотя бы одному подмножеству  ,
,  , скажем
, скажем  . Положим
. Положим 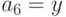 ,
,  . Вычеркнув цифры
. Вычеркнув цифры  и
и  из подмножеств
из подмножеств  ,
мы приходим к подмножествам
,
мы приходим к подмножествам  , для которых
, для которых  ,
, 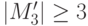 ,
,  ,
,  (
( ). Далее рассуждаем аналогично случаю 1: можно выбрать в
). Далее рассуждаем аналогично случаю 1: можно выбрать в  любую цифру
любую цифру  , в
, в  - цифру
- цифру  , отличную от
, отличную от 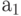 , и т. д., в
, и т. д., в  - цифру
- цифру  , отличную от
, отличную от  , а}
, а} , а}
, а}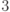 , а}
, а} .
.
Замечание. Можно рассмотреть общую задачу про  -значный код в алфавите из
-значный код в алфавите из  символов (в нашем случае
символов (в нашем случае  ) и доказать, что минимальное число попыток при
) и доказать, что минимальное число попыток при  будет равно
будет равно  , а при
, а при  оно равно
оно равно ![\left[\frac{m}{2}\right]+1](/sites/default/files/tex_cache/2c10f3e4cd88c3163698153b5223f014.png) .
.
Пример 6.24 (фольклор) А теперь Вы по заданию Центра должны проникнуть на сервер противника. Для этого Вам предстоит подобрать пароль к серверу методом "грубой силы" (последовательного перебора). Известно, что пароль назначается компьютером, регулярно меняется, а предыдущие пароли выглядели следующим образом (все буквы - латинские):
Какие выводы надо сделать, чтобы ускорить процесс подбора пароля? (Время имеет значение!).
Решение. Нетрудно заметить, что каждый из паролей является строкой из 8 латинских символов в верхнем и нижнем регистрах. Таким образом, пространство перебора имеет вид  . Мощность парольного пространства равна
. Мощность парольного пространства равна  .
.
Для ускорения процесса подбора пароля необходимо обнаружить какие-либо закономерности в последовательности известных паролей, чтобы сократить пространство перебора.
Из приведенных в условии задачи паролей видно, что в каждом из них есть хотя бы одна буква в нижнем регистре и хотя бы одна - в верхнем. Можно предположить, что генератор парольных последовательностей исключает возможность генерации пароля, состоящего только из строчных или только из заглавных букв. Это предположение естественно, так как это является одним из классических критериев стойкости пароля к подбору.
Таким образом, из подбора следует исключить строки, состоящие только из строчных или только из заглавных букв. Это позволит уменьшить пространство перебора на  попыток подбора.
попыток подбора.
Пример 6.25 ([3]) Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на 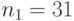 , полученный при этом остаток
, полученный при этом остаток  умножает на
умножает на  и получает число
и получает число  . После этого число
. После этого число  делит на
делит на  и полученный остаток
и полученный остаток  сохраняет на жестком диске. Например, если
сохраняет на жестком диске. Например, если  , то
, то  , соответственно,
, соответственно,  и
и  . Если пользователь ввел пароль
. Если пользователь ввел пароль  , и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа 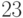 и
и 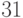 . То есть сначала стал делить на
. То есть сначала стал делить на  , а потом на
, а потом на 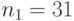 .
.
Известно, что в компьютере А и в компьютере Б хранится число  . Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке. Чей компьютер он взломает быстрее?
. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке. Чей компьютер он взломает быстрее?
Решение. Всего различных паролей 900 ( ). Вычислим, сколько из них дают в итоге число 5 по схеме пользователя А. Остаток 5 от деления на 23 дают натуральные числа 5, 28, 51. Больших чисел быть не может, так как
). Вычислим, сколько из них дают в итоге число 5 по схеме пользователя А. Остаток 5 от деления на 23 дают натуральные числа 5, 28, 51. Больших чисел быть не может, так как  . Так как 5 и 51 - нечетные числа, то
. Так как 5 и 51 - нечетные числа, то 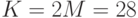 , значит,
, значит, 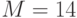 . Числа
. Числа  , дающие остаток 14 от деления на 31, имеют вид
, дающие остаток 14 от деления на 31, имеют вид  . Так как
. Так как  , то
, то  . В итоге получаем
. В итоге получаем  допустимых паролей (из 900 возможных).
допустимых паролей (из 900 возможных).
Если те же вычисления провести по схеме Б, то получим следующих претендентов для числа  : 5, 36. Следовательно,
: 5, 36. Следовательно,  и
и  , где
, где  . Итого 39 допустимых паролей.
. Итого 39 допустимых паролей.
Итак, вероятность взлома системы Б выше в  раза, чем у А.
раза, чем у А.
Пример 6.26 ([3]) Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 10 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б - 1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения 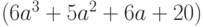 , где
, где  - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова.
Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - "ШИФРОВАНИЕ" или "КРИПТОГРАФ" - устойчивее к действию этой программы?
- число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова.
Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - "ШИФРОВАНИЕ" или "КРИПТОГРАФ" - устойчивее к действию этой программы?
Решение. В данной задаче необходимо вычислить все значения многочлена 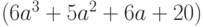 по модулю 31 для всех чисел от 0 до 30. Результаты вычисления представлены в следующей таблице:
по модулю 31 для всех чисел от 0 до 30. Результаты вычисления представлены в следующей таблице:
| 0 | А | 20 | 11 | Л | 28 | 22 | Ц | 27 | ||
| 1 | Б | 6 | 12 | М | 20 | 23 | Ч | 10 | ||
| 2 | В | 7 | 13 | Н | 20 | 24 | Ш | 25 | ||
| 3 | Г | 28 | 14 | О | 2 | 25 | Щ | 15 | ||
| 4 | Д | 12 | 15 | П | 2 | 26 | Ъ | 16 | ||
| 5 | Е | 26 | 16 | Р | 25 | 27 | Ы | 2 | ||
| 6 | Ж | 13 | 17 | С | 14 | 28 | Э | 9 | ||
| 7 | З | 9 | 18 | Т | 5 | 29 | Ю | 11 | ||
| 8 | И | 19 | 19 | У | 3 | 30 | Я | 13 | ||
| 9 | Й | 17 | 20 | Ф | 13 | |||||
| 10 | К | 8 | 21 | Х | 9 |
Таким образом, слово "ШИФРОВАНИЕ" зашифруется строкой чисел "25, 19, 13, 25, 2, 7, 20, 20, 19, 26". Перечисленные числа в качестве шифрсимволов встречаются соответственно 2, 1, 3, 2, 3, 1, 3, 3, 1 и 1 раза в таблице. Следовательно, число различных паролей, в зашифрованном виде имеющих вид "25, 19, 13, 25, 2, 7, 20, 20, 19, 26" будет равно  .
.
Для слова "КРИПТОГРАФ" мы после шифрования получаем последовательность "8, 25, 19, 2, 5, 2, 28, 25, 20, 13". Аналогичный подсчет дает число различных паролей, зашифровывающихся такой же последовательностью, равное  .
.
