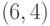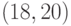|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Эллиптические кривые
4.1.4 Эллиптические кривые над конечным полем
Рассмотрим эллиптические кривые над конечным полем  ,
,  , где
, где  - простое число. В зависимости от характетистики поля уравнение кривой можно привести к одному из видов:
- простое число. В зависимости от характетистики поля уравнение кривой можно привести к одному из видов:

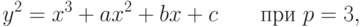
или к виду (4.2) при 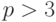 .
.
Особый интерес для криптографии представляет объект, называемый эллиптический группой по модулю  , где
, где  является простым числом.
является простым числом.
Далее мы, говоря об эллиптической кривой, если не оговорено противное, будем иметь в виду именно группу точек кривой над полем 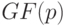 простого порядка
простого порядка  , заданной уравнением (4.2), причем
, заданной уравнением (4.2), причем  . Эту группу мы будем обозначать
. Эту группу мы будем обозначать 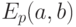 .
.
Пример 4.5 Пусть  . Рассмотрим эллиптическую кривую
. Рассмотрим эллиптическую кривую  .
.
В этом случае  и мы имеем
и мы имеем  , что удовлетворяет условиям эллиптической группы по модулю 23.
, что удовлетворяет условиям эллиптической группы по модулю 23.
Нас интересуют только целые значения от  до
до 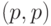 в квадранте неотрицательных чисел, удовлетворяющих уравнению по модулю
в квадранте неотрицательных чисел, удовлетворяющих уравнению по модулю  . В нашем случае список точек можно создать по следующим правилам.
. В нашем случае список точек можно создать по следующим правилам.
Теперь сравниваем числа в нижних строках табл. 4.1 и табл. 4.2. Число, попавшее в обе строки, определяет две точки кривой. Так, число 1 содержится и в нижней строке табл. 4.1, и в нижней строке табл. 4.2. Число 1 определяет точки 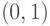 и
и  ; число 8 дает тоже две точки, находим по верхним строкам их координаты: это
; число 8 дает тоже две точки, находим по верхним строкам их координаты: это 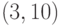 и
и 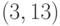 , и т. д. Таким образом, выбираем точки (отличные от
, и т. д. Таким образом, выбираем точки (отличные от  ), являющиеся элементами
), являющиеся элементами 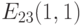 . Получаем табл. 4.3. Пара чисел
. Получаем табл. 4.3. Пара чисел  , для которой
, для которой 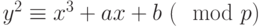 , включается в таблицу соответствий: это точка кривой.
, включается в таблицу соответствий: это точка кривой.
В криптографии применяются кривые, параметры которых являются большими (порядка 50 десятичных знаков) числами. В таких случаях перечисление всех точек кривой нереально за приемлемое время. Более того, даже определение количества точек кривой - весьма непростая задача.
Важной является
Теорема 4.1 (теорема Хассе) Пусть  - число точек на эллиптической кривой, определенной над
- число точек на эллиптической кривой, определенной над  . Тогда
. Тогда  .
.
4.1.5 Генерация точек эллиптической кривой
Для нахождения случайной точки эллиптической кривой  над полем простого порядка
над полем простого порядка  можно использовать следующий алгоритм:
можно использовать следующий алгоритм:
- Выбрать случайное
 .
. - Вычислить
 .
. - Вычислить символ Лежандра
 по
по  .
. - Если
 - квадратичный невычет, перейти к пункту 1.
- квадратичный невычет, перейти к пункту 1. - Вычислить
 - квадратный корень из
- квадратный корень из  по модулю
по модулю  (например, с помощью алгоритма Тонелли-Шенкса).
(например, с помощью алгоритма Тонелли-Шенкса).
Пример 4.6 Найти случайную точку эллиптической кривой  .
.
Решение. Пусть выбрано случайное число 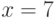 . Находим:
. Находим:  Вычисляем символ Лежандра-Якоби:
Вычисляем символ Лежандра-Якоби:

Следовательно,  не является квадратичным вычетом по модулю
не является квадратичным вычетом по модулю  ; выбираем другой
; выбираем другой  .
.
Пусть выбрано случайное число 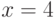 . Находим
. Находим  Вычисляем символ Лежандра-Якоби:
Вычисляем символ Лежандра-Якоби:

Итак,  - квадратичный вычет. Найдём корень из
- квадратичный вычет. Найдём корень из  по модулю
по модулю  .
.
Имеем:  . В алгоритме Тонелли-Шенкса получаем
. В алгоритме Тонелли-Шенкса получаем  . Мы уже знаем, что
. Мы уже знаем, что  является квадратичным невычетом; вычислим
является квадратичным невычетом; вычислим  . Вычисляем
. Вычисляем  При проверке видим, что
При проверке видим, что  Поэтому корнем из 22 будет число
Поэтому корнем из 22 будет число  . В самом деле,
. В самом деле, 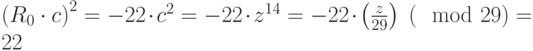 .
.
Итак, найдена точка  эллиптической кривой.
эллиптической кривой.
4.1.6 Сложение точек кривой над конечным полем
Проиллюстрируем примерами сложение точек кривой, построенной над конечным полем.
Пример 4.7 Выбрана кривая  , т. е.
, т. е.  . Найдем точку
. Найдем точку  .
.
Для нахождения  используем правила сложения точек эллиптической кривой (4.2).
используем правила сложения точек эллиптической кривой (4.2).
Вычисляем  :
:



Итак, мы нашли  . Теперь находим
. Теперь находим  :
:



Таким образом, мы нашли точку  .
.
4.1.7 Кратные точки
Данный алгоритм аналогичен алгоритму возведения в степень по модулю, см. параграф 1.2.2.
Рассмотрим алгоритм вычисления точки 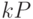 . Представим число
. Представим число  в двоичном виде:
в двоичном виде:

Далее, положим  ,
,  ,
, 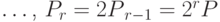 .
.
Откуда
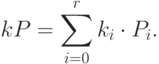
Таким образом, мы можем вычислить 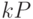 самое большее за
самое большее за  шагов, каждый из которых представляет собой сложение точек на кривой.
шагов, каждый из которых представляет собой сложение точек на кривой.
Пример 4.8 Найти  .
.
Представляем 100 в виде  Далее,
Далее,  ,
, 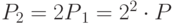 ,
, 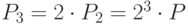 ,
, 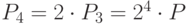 ,
,  ,
,  .
.
Теперь  .
.
Мы нашли точку 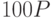 , произведя 6 удвоений и 2 сложения точек на кривой.
, произведя 6 удвоений и 2 сложения точек на кривой.
Пример 4.9 Найти точку  , кривая:
, кривая: 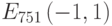 ,
, 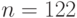 ,
,  .
.
Решение.

Пример 4.10 Найти порядок точки 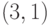 кривой
кривой  порядка
порядка 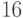 .
.
Решение. По теореме Лагранжа, порядок точки является делителем 16, то есть одним из чисел 2, 4, 8, 16. Пользуясь формулами (4.2), будем последовательно удваивать точку, пока не получим нейтральный элемент группы.

Следовательно, порядок точки 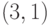 равен 4.
равен 4.
Пример 4.11 Найти порядок точки  кривой
кривой  порядка
порядка  .
.
Решение. Порядок точки является делителем числа 48, то есть одним из чисел: 2, 4, 8, 16, 3, 6, 12, 24. Нужно попробовать умножить точку на каждое из них. Расположим делители в узлах ориентированного дерева, где каждый потомок получается из родителя выполнением одной операции сложения точек. Пример такого дерева приведён на рис. 4.2.
Совершая обход этого дерева, будем получать кратные точки. Например, чтобы получить  , сначала удвоим точку четыре раза, получив
, сначала удвоим точку четыре раза, получив  , затем от
, затем от  придём по стрелке к
придём по стрелке к  .
.
Заметим, что вариантов построения такого дерева может быть много. Число ребер в дереве с 10 вершинами - всегда 9, а операция удвоения точки всегда быстрее сложения произвольных двух точек. Поэтому оптимальным будет проводить вычисления по дереву на рисунке рис. 4.3, содержащему наибольшее число удвоений.





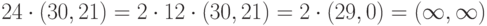
Теперь мы знаем, что порядок точки есть делитель числа 24, поэтому нам осталось пройти только те вершины дерева, в которых записаны делители числа 24. Например, вершину 16 мы рассматривать не будем.

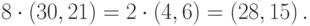
Итак, 24 - наименьшее число, при умножении точки на которое мы получим нейтральный элемент. Поэтому порядок точки равен 24.
Еще раз отметим, что во многих случаях определение порядка кривой является самостоятельной и весьма не простой задачей.
Список литературы
- Болоток А. А., Гашков С.Б., Фролов А. Б., Часовских А. А. Элементарное введение в эллиптическую криптографию - М.: КомКнига, 2006. - 328 с.
- Коблиц Н. Курс теории чисел и криптографии - М.: ТВП, 2003.

 (
( для
для  до
до 
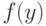
 (
( для
для