|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Эллиптические кривые
4.1.2 Операция на множестве точек эллиптической кривой
Будем временно полагать, что  , т. е. что эллиптическая кривая - обычная плоская кривая (с добавлением еще одной, бесконечно удалённой, точки
, т. е. что эллиптическая кривая - обычная плоская кривая (с добавлением еще одной, бесконечно удалённой, точки 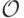 ). В графической интерпретации следует себе представлять ее расположенной на оси y в предельном направлении, определяемом все более "крутыми" касательными к кривой.
). В графической интерпретации следует себе представлять ее расположенной на оси y в предельном направлении, определяемом все более "крутыми" касательными к кривой.
Она является "третьей точкой пересечения" с кривой для любой вертикальной прямой: такая прямая пересекается с кривой в точках вида 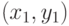 ,
, 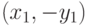 и в точке
и в точке 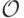 .
.
Определение 4.6 Пусть  - эллиптическая кривая над полем вещественных чисел и пусть
- эллиптическая кривая над полем вещественных чисел и пусть  и
и  - две точки на
- две точки на  . Определим точки
. Определим точки  и
и  по следующим правилам.
по следующим правилам.
- Точка
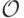 - нейтральный элемент по сложению. В следующих пунктах предполагается, что ни
- нейтральный элемент по сложению. В следующих пунктах предполагается, что ни  , ни
, ни  не являются точками в бесконечности.
не являются точками в бесконечности. - Точки
 и
и  имеют одинаковые
имеют одинаковые  -координаты, а их
-координаты, а их  -координаты различаются только знаком, т. е.
-координаты различаются только знаком, т. е. 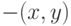 =
=  . Из уравнения кривой сразу следует, что
. Из уравнения кривой сразу следует, что  - также точка на
- также точка на  .
. - Если
 и
и  имеют различные
имеют различные  -координаты, то прямая
-координаты, то прямая  имеет с
имеет с  еще в точности одну точку пересечения
еще в точности одну точку пересечения  (за исключением двух случаев: когда она оказывается касательной в
(за исключением двух случаев: когда она оказывается касательной в  , и мы тогда полагаем
, и мы тогда полагаем  , или касательной в
, или касательной в  , и мы тогда полагаем
, и мы тогда полагаем  ). Определяем теперь
). Определяем теперь  как точку
как точку 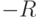 , т. е. как отражение от оси
, т. е. как отражение от оси  третьей точки пересечения. Геометрическое построение, дающее
третьей точки пересечения. Геометрическое построение, дающее  , приводится ниже в примере 4.2.
, приводится ниже в примере 4.2. - Если
 (т. е. координата
(т. е. координата  точки
точки  та же, что и y
та же, что и y  , а координата
, а координата  отличается лишь знаком), то полагаем
отличается лишь знаком), то полагаем 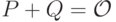 ("точке в бесконечности"; это является следствием п.1}).
("точке в бесконечности"; это является следствием п.1}). - Остается возможность
 . Тогда считаем, что
. Тогда считаем, что  - касательная к кривой в точке
- касательная к кривой в точке  . Пусть
. Пусть  - единственная другая точка пересечения
- единственная другая точка пересечения  с
с  . Полагаем
. Полагаем 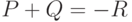 (в качестве
(в качестве  берем
берем  , если касательная прямая в
, если касательная прямая в  имеет "двойное касание", т. е. если
имеет "двойное касание", т. е. если  есть точка перегиба кривой).
есть точка перегиба кривой).
Пример 4.2 Рассмотрим эллиптическую кривую  =
=  - x в плоскости xOy (
рис.
4.1).
- x в плоскости xOy (
рис.
4.1).
Здесь приведен типичный случай сложения точек  и
и  . Чтобы найти
. Чтобы найти  , проводим прямую
, проводим прямую  и в качестве
и в качестве  берем точку, симметричную относительно оси
берем точку, симметричную относительно оси  третьей точке
третьей точке  , определяемой пересечением прямой
, определяемой пересечением прямой  и кривой. Если бы
и кривой. Если бы  совпадала с
совпадала с  , т. е. если бы нам нужно было найти
, т. е. если бы нам нужно было найти  , мы использовали бы касательную к кривой в
, мы использовали бы касательную к кривой в  : тогда точка
: тогда точка  симметрична третьей точке, в которой эта касательная пересекает кривую.
симметрична третьей точке, в которой эта касательная пересекает кривую.
(Взята эллиптическая кривая  )
)
В случае, когда основное поле не снабжено топологией (т.е. на нём не определено понятие предела), понятие касательной приходится заменять на прямую, проходящую через данную точку кривой, и формальные частные произоводные которой в этой точке совпадает с формальными частными производными уравнения кривой.
Обозначим  ,
,  - координаты точек
- координаты точек  ,
,  и
и  соответственно. Мы хотим выразить
соответственно. Мы хотим выразить 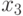 и
и 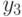 через
через 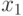 ,
, 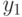 ,
, 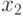 и
и 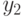 .
.
Если  ,
,  , либо
, либо  , то
, то  . В остальных случаях получаем:
. В остальных случаях получаем:
 |
( 4.1) |
Пример 4.3 Пусть 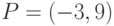 и
и  - точки на эллиптической кривой
- точки на эллиптической кривой 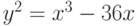 . Найти
. Найти  и
и  .
.
Решение. Подстановка 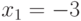 ,
,  ,
, 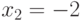 ,
,  в (4.1) при
в (4.1) при  дает
дает 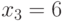 ,
,  . Непосредственной подстановкой координат точки
. Непосредственной подстановкой координат точки 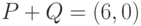 в уравнение кривой можно убедиться в том, что она также лежит на ней.
в уравнение кривой можно убедиться в том, что она также лежит на ней.
Для нахождения  используем второй вариант формулы (4.4) с
используем второй вариант формулы (4.4) с  . Подставляя
. Подставляя  ,
,  ,
, 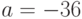 , находим
, находим 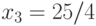 ,
, 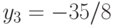 . Точка
. Точка  также принадлежит рассматриваемой кривой.
также принадлежит рассматриваемой кривой.
Теорема 4.2 Множество точек эллиптической кривой вместе с бесконечно удаленной точкой 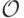 относительно операции, введённой в определении 4.6, образуют коммутативную группу.
относительно операции, введённой в определении 4.6, образуют коммутативную группу.
Если  - целое число, то, как и в любой коммутативной группе,
- целое число, то, как и в любой коммутативной группе,  обозначает сумму
обозначает сумму  точек
точек  при
при  и сумму
и сумму  точек
точек  , если
, если  .
.
4.1.3 Точки конечного порядка
Порядком  точки
точки  на эллиптической кривой называется такое наименьшее натуральное число, что
на эллиптической кривой называется такое наименьшее натуральное число, что  ; разумеется, такого конечного
; разумеется, такого конечного  может и не существовать, в этом случае мы будем говорить о точке бесконечного порядка. Часто требуется найти точки конечного порядка на эллиптической кривой, в особенности на эллиптических кривых, определенных над полем рациональных чисел
может и не существовать, в этом случае мы будем говорить о точке бесконечного порядка. Часто требуется найти точки конечного порядка на эллиптической кривой, в особенности на эллиптических кривых, определенных над полем рациональных чисел  .
.
Пример 4.4 Найти порядок точки  на
на  .
.
Решение. Применяя (4.1), находим, что 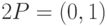 ,
,  . Поэтому
. Поэтому  и, следовательно,
и, следовательно,  . Тем самым порядок
. Тем самым порядок  может быть равен 2, 3 или 6. Но
может быть равен 2, 3 или 6. Но  , а если бы
, а если бы  имела порядок 3, то было бы
имела порядок 3, то было бы  , что неверно. Итак,
, что неверно. Итак,  имеет порядок 6.
имеет порядок 6.

