НОУ ИНТУИТ | Криптографические методы защиты информации. Лекция 1: Основы теории чисел

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 02.03.2017 | Доступ: свободный | Студентов: 2511 / 556 | Длительность: 21:50:00

Специальности: Программист, Администратор информационных систем, Специалист по безопасности, Архитектор программного обеспечения, Разработчик интернет-проектов

|

Вам нравится? Нравится 55 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

1.2.3 Функция Эйлера. Теоремы Эйлера и Ферма

Определение 1.13 Функция Эйлера $\varphi(m)$ - количество положительных чисел, не превосходящих и взаимно простых с .

Пример 1.13 Пусть . Взаимно простыми с 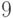являются числа: , , 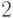, , 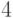, 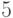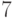. Так как количество этих чисел равно 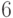, то $\varphi(9)=6$ .

Пример 1.14 Пусть . Взаимно простые с числа, меньшие - это ,,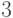, 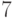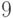. Поэтому $\varphi(10)=4$ .

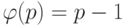Рассмотрим простое число . Все числа, меньшие , взаимно просты с ним. Итак, $\varphi(p)=p-1$ для простого .

Для чисел 9, 10 можно было вычислить значение функции Эйлера непосредственным перечислением чисел, взаимно простых с данным числом. Для числа 100 сделать это уже труднее, а для 10000 еще труднее. Оказывается, есть формула, позволяющая вычислять значение функции Эйлера достаточно просто.

Пусть задано каноническое разложение числа :

$m= {p}_{1}^{{\alpha }_{1}}\cdot{\dots}\cdot {p}_{k}^{{\alpha }_{k}}$ .

Тогда $\varphi(m)=m\cdot \left(1-\frac{1}{{p}_{1}}\right){\dots}\left(1-\frac{1}{{p}_{k}}\right)$ .

Пример 1.15

Так как 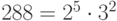$288= {2}^{5}\cdot {3}^{2}$ , то $\varphi(288)=288\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)=96$ .
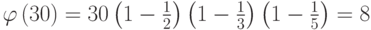Так как $30=2\cdot3\cdot5$ , то $\varphi\left(30\right)=30 \left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1-\frac{1}{5}\right)=8$ .
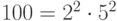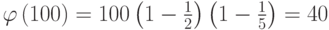Так как $100={2}^{2}\cdot{5}^{2}$ , то $\varphi\left(100\right)=100\left(1-\frac{1}{2}\right)\left(1-\frac{1}{5}\right)=40$ .

Теорема 1.15 (Эйлер) Если a - такое число, что , то ${a}^{\varphi (m)}\equiv 1~(mod \ m)$ .

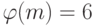Пример 1.16 Пусть , . Тогда $\varphi(m)=6$ , и по теореме Эйлера получаем: ${2}^{6}\equiv 1~(mod \ 9)$ . В справедливости этого равенства легко убедиться, если учесть, что ${2}^{6}=64$ .

Пример 1.17 Пусть 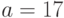, . Тогда $\varphi(32)=16$ , то по теореме Эйлера получаем: ${17}^{16}\equiv 1~(mod 32)$ . Убедиться в справедливости этого равенства непосредственным подсчётом было бы затруднительно.

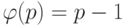Особенно простой вид теорема Эйлера принимает, если m=p - простое число. В этом случае $\varphi(p)=p-1$ , а потому получаем следующее утверждение:

Теорема 1.16 (малая теорема Ферма) Если - простое число и - целое число, такое, что 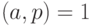, то ${a}^{p-1}\equiv 1~(mod \ p)$ .

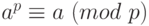Часто используется следствие малой теоремы Ферма, если - простое число, то для любого целого числа a имеет место сравнение: ${a}^{p} \equiv a~(mod \ p)$ .

Рассмотрим примеры на применение теорем Эйлера и Ферма.

Пример 1.18 Найдём остаток отделения ${3}^{28}$ на .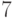

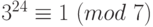Согласно теореме Ферма ${3}^{6}\equiv 1~(mod \ 7)$ , тогда ${3}^{24}\equiv 1~(mod \ 7)$ . Кроме того, 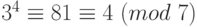${3}^{4}\equiv 81\equiv 4~(mod \ 7)$ . Тогда ${3}^{28}\equiv {3}^{24\cdot }{3}^{4} ~(mod \ 7)\equiv 4$ . Следовательно, искомый остаток r=4 .

Пример 1.19 Найдём остаток от деления 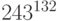${243}^{132}$ на .

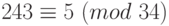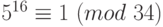Имеем: $243\equiv 5~(mod \ 34)$ . Тогда ${243}^{132}\equiv {5}^{132}~(mod \ 34)$ . Согласно теореме Эйлера ${5}^{\varphi (34)}\equiv 1~(mod \ 34)$ , или ${5}^{16}\equiv 1~(mod \ 34)$ . Далее делим 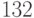132 на 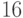, получим: $132=16\cdot8+4$ . Поэтому ${5}^{132}={\left({5}^{16}\right)}^{8}\cdot {5}^{4}\equiv {5}^{4}\equiv 625\equiv 13$ . Таким образом, ${243}^{132}\equiv 13~(mod \ 34)$ .

Следовательно, 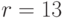r=13 .

Пример 1.20 Найдем остаток от деления числа 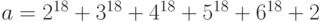$a=2^{18}+3^{18}+4^{18}+5^{18}+6^{18}+2$ на .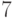

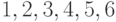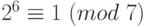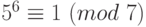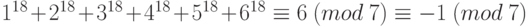Решение. Числа 1,2,3,4,5,6 взаимно просты с числом 7. По теореме Ферма, $1^{6}\equiv 1~(mod 7)$ , $2^{6}\equiv 1~(mod \ 7)$ , $3^{6}\equiv 1~(mod \ 7)$ , $4^{6}\equiv 1~(mod \ 7)$ , $5^{6}\equiv 1~(mod \ 7)$ , $6^{6}\equiv 1~(mod \ 7)$ . Возведем эти сравнения в третью степень и сложим, получим: $1^{18}+2^{18}+3^{18}+4^{18}+5^{18}+6^{18}\equiv 6~(mod \ 7)\equiv -1~(mod \ 7)$ . Следовательно, $1+1^{18}+2^{18}+3^{18}+4^{18}+5^{18}+6^{18}\equiv 0$ , то есть число делится на 7 без остатка.

Пример 1.21 Найти остаток от деления $7^{402}$ на .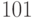

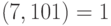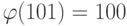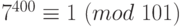Решение. Число 101 простое, (7,101)=1 , $\varphi(101)=100$ . По теореме Ферма, $7^{100}\equiv 1~(mod \ 101)$ . Возведем это сравнение в четвертую степень, получим: $7^{400}\equiv 1~(mod \ 101)$ . Умножим полученное сравнение на сравнение 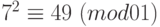$7^{2}\equiv 49~(mod \101)$ . Итак, 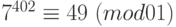$7^{402}\equiv 49~(mod \101)$ , то есть остаток равен 49.

Пример 1.22 Доказать, что $73^{12}-1$ делится на .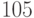

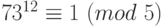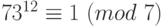Решение. Разложим на множители: $105=3\cdot5\cdot7$ . Далее, (73,3)=(73,5)=(73,7)=1 . По теореме Ферма, $73^{2}\equiv 1~(mod \ 3)$ , $73^{4}\equiv 1~(mod \ 5)$ , $73^{6}\equiv 1~(mod \ 7)$ . Возведем первое сравнение в шестую степень, второе в третью степень, третье во вторую, получим: $73^{12}\equiv 1~(mod \ 3)$ , $73^{12}\equiv 1~(mod \ 5)$ , $73^{12}\equiv 1~(mod \ 7)$ . А отсюда следует, что $73^{12}\equiv 1~(mod \ 105)$ , так как 105- наименьшее общее кратное чисел 3, 5, 7.

Определение 1.14 Число называется обратным к по модулю , если $a\cdot b\equiv 1(mod \ m)$ . Пишут: $b= a^{-1} ~(mod \ m)$ .

Например, 3 обратно к 2 по модулю 5, так как $2\cdot3\equiv 1~(mod \ 5)$ . Заметим, что обратное к по модулю можно найти лишь в случае (a,m)=1 . Если (a,m)=d>1 , то обратный к по модулю не существует. Например, обратного к 2 по модулю 10 не существует: при умножении любого числа на 2 мы не получим 1 по модулю 10. Если модуль сравнения - простое число, то обратный элемент есть для каждого числа.

Пример 1.23 Найдем число, обратное к 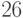по модулю .

Числа 26 и 49 взаимно просты, поэтому искомое число существует. Реализуем расширенный алгоритм Евклида для чисел 26 и 49.

Имеем: $49=1 \cdot 26+23$ ,

$26=1 \cdot 23+3$ ,

$23=7 \cdot 3+2$ ,

$3=1 \cdot 2+1$ .

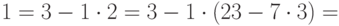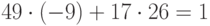И теперь $1=3 - 1 \cdot 2=3-1 \cdot (23-7 \cdot 3)=%-1 \cdot 23+8 \cdot 3=-1 \cdot 23+8 \cdot (26-1 \cdot 23)=%8 \cdot 26-9 \cdot 23=8 \cdot 26-9 \cdot (49-1 \cdot 26)=%-9 \cdot 49+17 \cdot 26$ . Итак, $49 \cdot (-9)+17 \cdot 26=1$ . То есть $26 \cdot 17\equiv 1~(mod \ 49)$ . Таким образом, число 17 является обратным к 26 по модулю 49.

1.2.4 Решение сравнений

Сравнение с одним неизвестным имеет вид

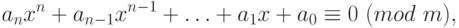${a}_{n}{x}^{n}+{a}_{n-1}{x}^{n-1}+{\dots}+{a}_{1}x+{a}_{0} \equiv 0~(mod \ m),$

( 1.3)

где $m \in \mathbb{N}$ , m>1 . Если ${a}_{n}$ не делится на , то называется степенью сравнения (1.3).

Определение 1.15 Решением сравнения (1.3) называется всякое целое число ${x}_{0}$ , для которого ${a}_{n}{x}_{0}^{n}+{a}_{n-1}{x}_{0}^{n-1}+{\dots}+{a}_{0} \equiv 0 ~(mod \ m)$ .

Если ${x}_{0}$ удовлетворяет сравнению (1.3), то, согласно свойству 11 сравнений, этому сравнению будут удовлетворять все целые числа, сравнимые с ${x}_{0}$ по модулю . Поэтому все числа, сравнимые по модулю с ${x}_{0}$ , будем рассматривать как одно решение. Другими словами, решениями сравнения (1.3) будут классы чисел. Например, $\bar{1}$ - это класс единицы, то есть все числа, сравнимые с 1, $\bar{2}$ - класс числа 2, то есть все числа, сравнимые с 2, т.д. И фразу "данное сравнение имеет 2 решения" надо понимать так: данному сравнению удовлетворяют два класса чисел. Как отмечалось выше, эти классы не имеют общих элементов. В дальнейшем мы записываем какое-либо число - представитель класса без черты сверху, называя это число решением.

Сравнения, множества решений которых совпадают, называются равносильными.

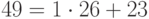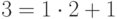Дальше >>

Авторизоваться

Криптографические методы защиты информации

Основы теории чисел

1.2.3 Функция Эйлера. Теоремы Эйлера и Ферма

1.2.4 Решение сравнений

Вопросы и ответы