Опубликован: 12.02.2014 | Доступ: свободный | Студентов: 924 / 239 | Длительность: 11:22:00
Тема: Программирование
Специальности: Программист
Лекция 11:
Парсеры
11.3. Поиск наибольшего общего унификатора
В данном параграфе реализуется алгоритм поиска наибольшего общего унификатора двух термов (или атомарных формул). Формулы подаются программе в виде двух строк. Парсер преобразует их в термы специального вида, которые и поступают на вход алгоритма.
Грамматика исходных формул описывается следующим образом:
term ::= var | const | fun [(] termlist [)] termlist ::= term | term [,] termlist
Переменные пишутся с прописной буквы, а константы, предикатные и функциональные символы — со строчной, например,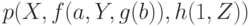 
.
Алгоритм поиска наибольшего общего унификатора термов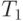 
и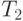 
с помощью двух стеков 
и 
описан в [9]. Он заключается в следующем. Вначале в помещается пара термов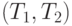 
, стек пуст. Алгоритм начинается с шага 1.
- Если стек пуст, то алгоритм завершает свою работу и унификатор полагается равным , иначе совершается переход к шагу 2.
-
Из
извлекается пара термов 
. Возможны случаи:- если
— переменная, а 
— терм, не содержащий , то в и выполняется замена на , из удаляются пары совпадающих термов, в добавляется пара термов и выполняется переход к шагу 1; - если — переменная, а — терм, не содержащий , то в и выполняется замена на , из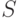
удаляются пары совпадающих термов, в добавляется 
и выполняется переход к шагу 1; - если и — пара совпадающих переменных или констант, то выполняется переход к шагу 1;
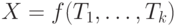- если
и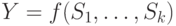 
, то в добавляются пары термов 
и выполняется переход к шагу 1; - в остальных случаях алгоритм завершает работу — термы не унифицируемы.
- если
open core, console, string
domains
term = var(string Var); c(string Const); f(string Name, term*).
% парсер
class predicates
scan: (string) -> string*.
parser: (string*, term [out], string* [out]) determ.
parser: (string*, term* [out]) -> string* determ.
checkName: (string) determ.
clauses
scan(Str) = [Tok | scan(RestStr)]:-
frontToken(Str, Tok, RestStr),
!.
scan(_) = [].
parser([S, "(" | L], f(S, TermList), Rest):- !,
checkName(S),
[")" | Rest] = parser(L, TermList).
parser([S | L], var(S), L):-
isName(S),
Ch = frontChar(S),
Ch = charUpper(Ch),
!.
parser([S | L], c(S), L):-
(_ = tryToTerm(unsigned, S); _ = tryToTerm(real, S);
checkName(S)),
!.
parser(["," | L], TermList) = parser(L, TermList):- !.
parser(L, [Term | TermList]) = parser(Rest, TermList):-
parser(L, Term, Rest),
!.
parser(L, []) = L.
checkName(S):-
Ch = charToString(frontChar(S)),
hasAlpha(Ch),
isLowerCase(Ch).
% поиск наибольшего общего унификатора
class predicates
unify: (term, term) -> term* determ.
unif: (term*, term*) -> term* determ.
subterm: (term, term) determ.
replace: (term*, term, term) -> term*.
delete: (term*) -> term*.
put: (term*, term*, term*) -> term* determ.
clauses
unify(X, Y) = unif([X, Y], []).
unif([var(X), var(X) | L], Subst) = unif(L, Subst):- !.
unif([c(X), c(X) | L], Subst) = unif(L, Subst):- !.
unif([var(X), Y | L], Subst) = unif(replace(L, var(X), Y),
[var(X), Y | delete(replace(Subst, var(X), Y))]):- !,
not(subterm(var(X), Y)).
unif([Y, var(X) | L], Subst) = unif([var(X), Y | L], Subst):- !.
unif([f(N, TL1), f(N, TL2) | L], Subst) = unif(L1, Subst):-
L1 = put(TL1, TL2, L).
unif([], Subst) = Subst.
subterm(X, X):- !.
subterm(X, f(_, L)):-
list::exists(L, {(H):- subterm(X, H)}).
replace([X | L], X, Y) = [Y | replace(L, X, Y)]:- !.
replace([H | L], X, Y) = [H | replace(L, X, Y)].
replace([], _, _) = [].
delete([X, X | L]) = delete(L):- !.
delete([X, Y | L]) = [X, Y | delete(L)]:- !.
delete(_) = [].
put([X | L1], [Y | L2], L) = put(L1, L2, [X, Y | L]).
put([], [], L) = L.
% преобразование в строку
class predicates
s: (term) -> string.
toStr: (term*) -> string*.
clauses
s(var(X)) = X:- !.
s(c(X)) = X:- !.
s(f(N, L)) = format("%(%)", N,
concatWithDelimiter(list::map(L, {(T) = s(T)}), ", ")).
toStr([X, Y | L]) = [format("% = %", s(X), s(Y)) | toStr(L)]:- !.
toStr(_) = [].
run():-
S1 = "p(X, f(b, Y), g(a, a), k(h(1, 2, 3)), U)",
S2 = "p(a, f(b, a), g(a, Y), k(Z), V)",
parser(scan(S1), Term1, _),
parser(scan(S2), Term2, _),
Subst = unify(Term1, Term2),
writef("%\n%\n\n%", s(Term1), s(Term2),
concatWithDelimiter(toStr(Subst), ", ")),
fail;
_ = readLine().
Пример
11.3.
Разбор термов. Реализация алгоритма поиска НОУ
Предикат charToString преобразует символ (char) в строку (string), предикат isLowerCase истинен, если все символы строки имеют нижний регистр, предикат hasAlpha истинен, если строка состоит только из букв, предикат exists проверяет, имеется ли в списке элемент, удовлетворяющий заданному условию.
Упражнение 2. Реализуйте в программе, приведенной в листинге 11.3, возможность использования анонимных переменных (напомним, что они унифицируются с любыми термами, но не принимают значений).
Упражнения
- Напишите программу, которая выполняет перевод простых английских предложений на немецкий язык.
- Напишите программу, которая разбирает и вычисляет выражения с комплексными числами.
- Напишите программу, которая разбирает и упрощает тригонометрические выражения.
- Напишите программу, которая выполняет действия над многочленами — сложение, умножение на число, умножение, деление с остатком.
- Напишите программу, которая строит польскую запись арифметических выражений.
- Требуется так расставить между шестью девятками знаки сложения, вычитания умножения и деления, чтобы в результате вычисления получилось число 100.
- Требуется получить число 24 из трех пятерок и единицы, расставив между ними знаки сложения, вычитания умножения, деления и скобки.
- Напишите программу, которая выполняет разбор и линеаризует списки вида "[0, [1, [2, 3, [4]]], 5]". Список подается на вход в виде строки. Линейный список также выдается в виде строки.
