Квантовые процессоры на основе спинового магнитного резонанса

Основные положения лекции 10

Во внешнем магнитном поле с индукцией разрешенное стационарное состояние частицы со спином расщепляется на разрешенных состояний. Энергетическое расстояние между разрешенными уровнями энергии , где – магнитный момент частицы. Из-за наличия у частицы, кроме магнитного, еще и механического момента вращения (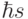) имеет место прецессия обеих моментов вокруг направления магнитного поля с частотой , где – гиромагнитное отношение. Если перейти в подвижную систему координат (ПСК), вращающуюся вокруг направления магнитного поля с частотой прецессии, то в ней вектор состояния кубита является неподвижным.

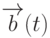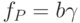Кроме постоянного магнитного поля на спиновый кубит можно подействовать переменным поперечным магнитным полем , вектор индукции которого вращается вокруг с частотой прецессии. В ПСК этот вектор тоже является неподвижным и вызывает дополнительную прецессию магнитного момента вокруг вектора с частотой Раби , которая намного меньше, чем . Регулируя момент включения и длительность импульса резонансного поперечного магнитного поля 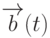, можно довольно точно манипулировать ориентацией магнитного момента , а, следовательно, и квантовым состоянием спинового кубита, т.е. выполнять над ним все требуемые квантовые логические операции.

Когда частота радиочастотного импульса поперечного магнитного поля 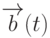значительно отличается от резонансной для данного спинового кубита, то такие импульсы практически не влияют на состояние этого кубита. Это позволяет манипулировать разными кубитами независимо, если их резонансные частоты заметно отличаются.

В квантовом процессоре, предложенном Б. Кейном, роль спиновых кубитов играют ядра атомов фосфора со спином ½. Основой процессора является пластина изотопно чистого кремния (). Четыре из 5 электронов внешней оболочки атома фосфора образуют ковалентные связи с соседними атомами кремния. Их спины попарно скомпенсированы. Внешний, 5-й, электрон образует локальный примесный донорный уровень с достаточно большим радиусом атомной орбитали (АО). Спиновый магнитный момент этого электрона взаимодействует и с магнитным моментом ядра , и с собственным орбитальным магнитным моментом, и с внешним магнитным полем, и с соседними кубитами (атомами фосфора ). Над каждым кубитом формируют металлический электрод A, электрически изолированный слоем окисла. Для выполнения квантовой логической операции над кубитом на соответствующий электрод A подают определенный потенциал, смещающий и деформирующий АО внешнего электрона. Из-за этого изменяется энергия взаимодействия магнитного момента ядра с магнитным моментом электрона, и соответственно изменяется резонансная частота прецессии спина ядра . И дальше с помощью последовательности радиоимпульсов с частотой, резонансной именно при этом потенциале, выполняют нужную логическую операцию. Другие кубиты, имеющие существенно другие резонансные частоты, на эти манипуляции не откликаются. Для выполнения двухкубитных квантовых логических операций используют металлические электроды B, размещенные над промежутками между кубитами.

ЯМР квантовый процессор, предложенный Б. Кейном, теоретически позволяет реализовать квантовые регистры из тысяч кубитов, обеспечивая при этом возможность индивидуально управлять каждым кубитом и небольшими группами кубитов.

Однако при считывании конечного состояния кубитов сигналы оказались довольно таки слабыми, что предопределяет значительные погрешности считывания. Чтобы повысить надежность считывания, предложена идея использования "ансамблевого" ЯМР квантового процессора. При этом на пластине бесспинового кремния создается много рядов спиновых кубитов – целый ансамбль квантовых регистров. Благодаря тысячам параллельно функционирующих квантовых регистров их конечное состояние становится возможным считывать с помощью хорошо отработанных методов. Параллельная работа ансамбля одинаковых квантовых регистров уменьшает также влияние многих технологических неточностей (незначительных технологических отклонений в расположении атомов , в ширине управляющих электродов и т.п.).

Интересен вариант ЯМР квантового процессора, в котором в качестве кубитов используют атомы со спином ядра 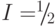, капсулированные внутри фуллерена. Атомы изотопов 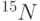или , капсулированные внутри фуллерена , могут иметь лишь два значения ядерного магнитного квантового числа 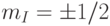. Суммарный электронный спин у них , и поэтому магнитное квантовое число электронной оболочки такого атома может принимать 4 разные значения . Во внешнем магнитном поле основной энергетический уровень такого кубита расщепляется на 8 разрешенных энергетических уровней. Резонансные переходы между этими уровнями под действием микроволновых и радиоимпульсов и используют для установки нужного состояния кубитов, для выполнения квантовых логических операций и для считывания конечного состояния. Квантовый регистр состоит из цепи молекул или , иммобилизованных на диэлектрической подложке и выстроенных в одну линию с периодом расположения 3,5 нм. Кроме постоянного однородного создается также градиентное магнитное поле, благодаря которому на каждый кубит действует свое по величине дополнительное магнитное поле. И поэтому каждый кубит имеет свою частоту электронного спинового резонанса, что позволяет адресно изменять состояние каждого кубита. Для выполнения двухкубитных квантовых логических операций используют взаимодействие электронных магнитных моментов соседних кубитов. Преимуществами этого варианта ЯМР квантового процессора являются его "молекулярно малые" размеры и то, что здесь удалось обойтись без управляющих электродов. Однако проблема считывания конечного состояния кубитов остается пока не решенной.

Из-за относительно низкой частоты прецессии ядерных спинов (порядка 100 МГц) и соответственно малой частоты Раби квантовый процессор на ЯМР работает относительно медленно. В отличие от этого частота прецессии в условиях электронного спинового резонанса (ЭСР) в магнитных полях порядка 2-3 Тл в сотни раз выше (50-100 ГГц). Поэтому и квантовые логические операции на электронных спиновых кубитах выполняются намного быстрее. В одном из предложенных квантовых процессоров на основе ЭСР в качестве кубита используется магнитный момент внешнего ("донорного") электрона атома . Такие атомы размещаются в слое с составом многослойной гетероструктуры, которую формируют так, чтобы обеспечить выполнение двух важных требований. Одно из них – сделать так, чтобы донорные электроны кубитов оказались в "потенциальной яме", не позволяющей им перемещаться по вертикали за границы барьерных слоев. Второе требование заключается в том, чтобы изменения электрического потенциала на управляющем электроде позволяли существенно влиять на резонансную частоту соответствующего кубита. Благодаря этому появляется возможность селективно выполнять квантовые логические операции над каждым из сотен отдельных кубитов, а также 2- и 3-кубитные логические операции. Для считывания состояния кубитов после окончания квантовых вычислений в одном из гетероэпитаксиальных слоев под кубитами формируют полевые транзисторы с каналом проводимости, размещенным точно под атомом . Квантовый процессор на основе ЭСР имеет такие преимущества над ЯМР полупроводниковыми квантовыми процессорами: квантовые логические операции выполняются в сотни раз быстрее; не требуется изотопная очистка полупроводника; достаточна лишь одна система управляющих электродов; упрощается процесс считывания информации при завершении квантовых вычислений.

К сожалению, во всех вариантах спинового квантового процессора пока что не удалось преодолеть декогерентизацию настолько, чтобы в регистре из тысячи кубитов достигалось безошибочное выполнение требуемых 10⁴–10⁵ квантовых операций. Этого удается достичь пока что лишь на квантовых регистрах с ограниченным числом кубитов.

Набор для практики

Вопросы для самоконтроля

1. Почему в сильном внешнем магнитном поле возникает прецессия магнитного момента частицы вокруг направления поля? От чего зависит угловая частота прецессии? Напишите и объясните соответствующую формулу.
2. Что такое "ПСК"? Какими параметрами описывается в ней квантовое состояние кубита?
3. Как создается "резонансное" поперечное магнитное поле? Изобразите схему и объясните принцип ее работы.
4. Что такое "частота Раби"? За счет чего она возникает? Напишите и объясните формулу для расчета частоты Раби.
5. Почему важен момент включения резонансного поперечного магнитного поля относительно фазы ларморовой прецессии? Объясните процессы, которые происходят при двух разных моментах включения.
6. Что такое "-импульс"? Что такое "-импульс"? Как ведет себя в этих случаях магнитный момент спинового кубита?
7. Как с помощью радиочастотных импульсов удается манипулировать состоянием спинового кубита? Как это связано с выполнением однокубитных квантовых логических операций?
8. Что происходит с магнитным моментом спинового кубита, когда частота радиоимпульсов значительно отличается от резонансной? Как это влияет на квантовое состояние кубита? Какие возможности вследствие этого появляются?
9. Благодаря чему можно работать не с циркулярным, а с линейным поперечным радиочастотным полем, упрощая таким образом конструкцию спинового квантового процессора?
10. Как устроен ЯМР квантовый процессор, предложенный Б. Кейном?
11. Какие положительные стороны имеет этот квантовый процессор? В чем заключаются его недостатки?
12. Что такое "ансамблевый" ЯМР квантовый процессор? В чем заключаются его преимущества?
13. Как устроен ЯМР квантовый процессор, в котором кубитами являются атомы, капсулированные внутри фуллерена? Опишите кратко его структуру и работу.
14. Какие преимущества имеют квантовые процессоры на электронном спиновом резонансе (ЭСР) над ЯМР квантовыми процессорами? И почему?
15. Как устроен ЭСР квантовый процессор, предложенный Ди Винченцо? Изобразите его структуру и объясните назначение основных гетероэпитаксиальных слоев.
16. Назовите основные причины декогерентизации в спиновых квантовых процессорах.