|
Добрый день!
Скажите, пожалуйста,планируется ли продолжение курсов по нанотехнологиям? Спасибо, Евгений
|
Оценка производительности и живучести МКМД-БИТ-потокового предпроцессора системы астронавигации
8.1. Описание предметной области и системы преобразований МКМД-бит-потокового субпроцессора слежения за "центром масс" астроориентира
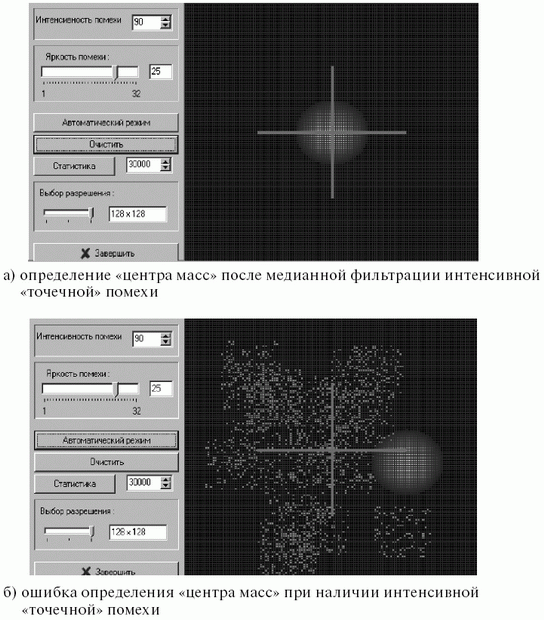
В основе решения задач автоматической астронавигации лежит определение пространственного положения линии визирования от космического летательного аппарата (КЛА) до центра некоторой "неподвижной" яркой звезды, используемой в качестве астроориентира. В идеале с помощью обработки бинарного видеоизображения звездного пространства можно достаточно четко "провести" линию визирования до центра астроориентира (рис. 8.1-а). Однако в звездном пространстве существуют не только астроориентиры, но и мириады звезд (рис. 8.1-б), которые для алгоритма обработки бинарного изображения представляют собой "точечную" помеху, способную сместить вычисленный "центр масс" даже очень крупного астроориентира. Такого рода помехи наиболее эффективно фильтруются медианным фильтром (см. раздел 4.5 [290]), апертура которого должна более чем в два раза превышать площадь каждой яркой звезды, бли зко примыкающей в пространстве к астроориентиру.
Для решения такого рода задач на борту КЛА необходимо иметь видеокамеры (желательно по одной на астроориентир, чтобы жестко связать их положение с осями КЛА), которые формируют бинарные (черно-белые) изображения требуемого участка звездного пространства. Апертура таких видеокамер не должна быть очень большой (не более 128*128 пикселей), чтобы за счет малого "угла зрения" снизить паразитные влияния остальных звезд.
Частота определения собственного положения в пространстве КЛА невелика, как невелика и сложность задачи обработки такого изображения. Поэтому современные ЦПОС способны справиться с решением в реальном времени подобного рода задач. Однако высочайшая ответственность за успех космической экспедиции и достаточно продолжительное негативное влияние на (Б)ВС жестких космических излучений и других внешних воздействующих факторов выдвигают на первый план требование к (сверх)высокой живучести вычислительных комплексов, отвечающих за решение задач астронавигации, а значит, и за эффективность автономного управления полетом КЛА.
- определение "центра масс" после медианной фильтрации интенсивной "точечной" помехи
- ошибка определения "центра масс" при наличии интенсивной "точечной" помехи
увеличить изображение
Рис. 8.1. Влияние звездного пространства на точность визирования "центра масс" астроориентира
Аналогичные задачи решаются при посадке ЛА в плохих погодных условиях на подвижное основание, при дозаправке в воздухе группы самолетов и т. д. Но здесь уже требуются как (сверх)высокая (109-1012 оп/ сек) производительность, так и (сверх)высокая отказоустойчивость при выполнении особо сложных маневров, сопряженных с опасностью потери ЛА или гибелью экипажей.
Задачи, решаемые такими пассивными системами микро- и астронавигации, содержат достаточно полный набор функций (слов-инструкций), который можно рассматривать как представительную смесь, объективно
характеризующую возможности работы системы обеспечения живучести практически всех МКМД-бит-потоковых субпроцессоров. Поэтому полученные для такого проблемно-ориентированного субпроцессора характеристики системы обеспечения живучести с высокой степенью достоверности можно распространить на весь МКМД-бит-потоковый субпроцессорный тракт (см. рис. 4.5 раздела 4.2).
Таким образом, в субпроцессором тракте (Б)ВС КЛА требуется решить в реальном времени следующие задачи:
- медианную фильтрацию кадров для устранения "точечных" помех, отвечающих "скользящему окну" размером 5x5 пикселей;
- нахождение "центра масс" для каждого из 5-10 астроориентиров;
- определение рассогласования между текущим направлением движения и заданным;
- формирование сигналов управления.
Ориентированный на решение перечисленных задач субпроцессорный тракт (Б)ВС КЛА должен иметь пред- и сопроцессор, на первый из которых возлагаются первые две задачи, а на второй - последние. Покажем, что основное достоинство такой схемы построения отечественных (Б)ВС состоит в том, что при этом повышается не только производительность, но и вычислительная устойчивость, устойчивость к отказам, а с ними и отказобезопасность всего БЭО отечественных (К)ЛА.
При разработке МКМД-бит-потокового предпроцессора слежения за "центром масс" астроориентира будем считать, что исходное видеоизображение имеет размеры 128x128 черно-белых пикселей 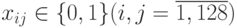 .
Такие размеры обрабатываемого видеоизображения обеспечивают приемлемую угловую избирательность порядка 10о-15о, которая, с одной стороны, снижает влияние естественных и искусственных видеопомех, а с другой стороны - обеспечивает достаточно высокую точность определения угловых координат "центра масс" астроориентира порядка 0,08о-0,12о. Вычисленные линейные координаты "центра масс" фигуры, идентифицированной как астроориентир, по отношению к центру плоского (двумерного) черно-белого изображения, должны быть жестко связаны с продольной и другими осями (К)ЛА,
по отношению к которым и вырабатываются управляющие воздействия извне и со стороны собственной системы автоматического управления (САУ).
При этом система обеспечения живучести субпроцессора должна обнаружить в темпе реального времени все функционально значимые отказы аппаратуры.
.
Такие размеры обрабатываемого видеоизображения обеспечивают приемлемую угловую избирательность порядка 10о-15о, которая, с одной стороны, снижает влияние естественных и искусственных видеопомех, а с другой стороны - обеспечивает достаточно высокую точность определения угловых координат "центра масс" астроориентира порядка 0,08о-0,12о. Вычисленные линейные координаты "центра масс" фигуры, идентифицированной как астроориентир, по отношению к центру плоского (двумерного) черно-белого изображения, должны быть жестко связаны с продольной и другими осями (К)ЛА,
по отношению к которым и вырабатываются управляющие воздействия извне и со стороны собственной системы автоматического управления (САУ).
При этом система обеспечения живучести субпроцессора должна обнаружить в темпе реального времени все функционально значимые отказы аппаратуры.
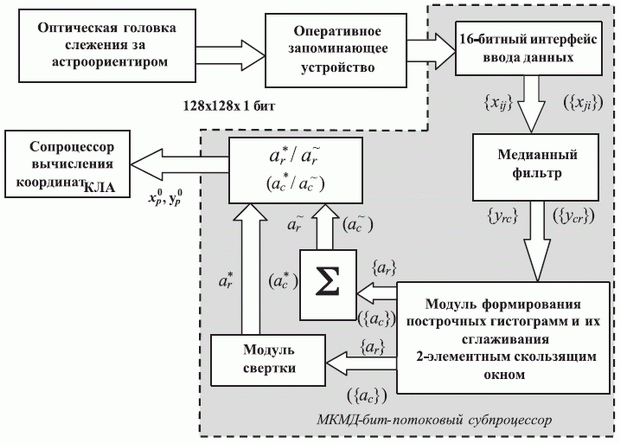
Структурно-функциональная схема канала обработки астронавигационной информации приведена на рис. 8.2, а укрупненный алгоритм его работы имеет вид:
- Обработать изображение
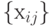 медианным фильтром со скользящим
окном размером 5x5 пикселей. В результате получим изображение
медианным фильтром со скользящим
окном размером 5x5 пикселей. В результате получим изображение 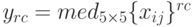 , в котором индексы
, в котором индексы  ,
,  соответствуют положению центрального элемента "скользящего окна" и связаны с индексами
соответствуют положению центрального элемента "скользящего окна" и связаны с индексами  ,
,  строк и столбцов исходного изображения правилом
строк и столбцов исходного изображения правилом 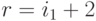 , а
, а 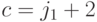 , где
, где 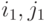 - координаты левого верхнего угла "скользящего окна".
- координаты левого верхнего угла "скользящего окна". - Подавить паразитные взаимодействия элементов "скользящего окна" при его переходе со строки на строку:
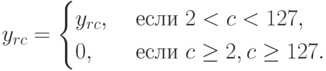
- Составить гистограмму по строкам
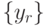 , где
, где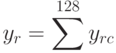
- Обработать гистограмму двухэлементным скользящим окном
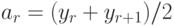
- Обнулить паразитные взаимодействия в двухэлементном "скользящем окне" при переходе от одного кадра обрабатываемого изображения к другому:

- Выполнить свертку вектор-столбца
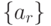 по правилу
по правилу
- Вычислить суммарную яркость обрабатываемого изображения:
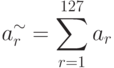
- Определить координату
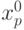 центра масс изображения по отношению к его верхнему левому углу:
центра масс изображения по отношению к его верхнему левому углу: 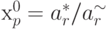 , где
, где  - номер фотоприемника, для которого найдена координата.
- номер фотоприемника, для которого найдена координата.
Для вычисления координаты 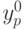 матрица
матрица  транспонируется и полученная матрица
транспонируется и полученная матрица  обрабатывается аналогичным образом, где после первого этапа вычислений формируется матрица
обрабатывается аналогичным образом, где после первого этапа вычислений формируется матрица 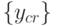 , после четвертого этапа - вектор-столбец
, после четвертого этапа - вектор-столбец 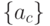 , а на восьмом этапе -
, а на восьмом этапе - 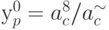
Бит-матрица используется с разделением времени как при определении каждой координаты "центра масс" астроориентира 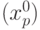 и
и 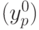 , так и при обработке изображений от каждого из пяти фотоприемников.
, так и при обработке изображений от каждого из пяти фотоприемников.